广义Boussinesq方程的正则性准则*

邱 华，姚正安

(1.华南农业大学数学系，广东广州510642;

2.中山大学数学与计算科学学院，广东广州 510275)

在本文，我们考虑如下三维广义Boussinesq方程的柯西问题:

其中u=(u1，u2，u3)表示流体速度，P为压力，θ为温度，μ为黏性系数，κ为热扩散系数，e3=(1，0，0)T，u=(u1，u2，u3)，u0与θ0分别为在t=0给定的流体初始速度与初始温度，且满足▽·u0=0。

Boussinesq方程不仅在大气科学中有着重要应用［1］，而且在地球物理科学中亦有着广泛应用［2］。广义Boussinesq方程是将通常的Boussinesq方程中的拉普拉斯算子－Δ用分数次拉普拉斯算子(－Δ)α替换得到，这种研究分数次方程的方法可参见Wu等［3］对广义MHD方程的研究。若α=β=1，广义Boussinesq方程 (1)即为通常的 Boussinesq方程。在二维情形，Cannon与 DiBenedetto［4］得到了在α=β=1和μ，κ＞0关于整体时间的正则性解;然而，当μ=κ=0时，该方程解的正则性问题仍然是数学流体力学中的公开问题［5－6］。最近，众多学者考虑了当α=β=1无黏性或者无扩散情形下的解的整体正则性问题，相关文献可参见文献 ［7－9］。另外，对于通常的三维 Boussinesq方程，Ishimura和Morimoto［10］给出了如下光滑解的正则性准则

最近，邱华，杜毅与姚正安［11］得到了三维 Boussinesq方程的 Serrin类正则性准则。而对于广义Boussinesq方程的柯西问题，许孝精得到了二维广义Boussinesq方程在1≤α+β≤2条件下解的存在唯一性，并给出了正则性准则。

本文，我们考虑三维广义Boussinesq方程的正则性问题，给出了该类方程的两个正则性准则。本文的第一个主要结论是三维广义Boussinesq方程在Sobolev空间意义下的正则性准则，结果如下:

则解(u，θ)在时刻t=T处仍然是光滑的，其中

进一步地，我们给出了在Morrey空间意义下三维广义Boussinesq方程的正则性准则，结果陈述如下:

定理2 假设0＜α=β≤1，流体的初始速度与温度(u0，θ0)∈H1(R3)，且(u，θ)为问题 (1)在0≤t＜T时的光滑解。若

则解(u，θ)在时刻t=T处仍然是光滑的，其中

注1 当α=1时，定理1的条件变为

这包含了Ishimura与 Morimoto［10］的结果 (2)。

进一步地，根据Biot-Savart定律与Lp(R3)间上Riesz变换的有界性 (这里1＜p＜+∞ )(参见文献 ［13］)，我们有

于是，我们可得如下推论:

则解(u，θ)在时刻t=T处仍然是光滑的，其中

推论2 假设0＜α=β≤1，流体的初始速度与温度 (u0，θ0)∈H1(R3)，ω0=curlu0∈L2(R3)，且(u，θ)为问题 (1)在0≤t＜T时的光滑解。若

则解(u，θ)在时刻t=T处仍然是光滑的，其中

本文第二节给出一些基本定义与定理。第三节证明定理1。第四节证明定理2。

1 预备

在本小节，我们给出 Morrey空间的相关定义以及证明过程中需要的引理。

其中B(x，R)是R3中以x为中心且半径为R的球。

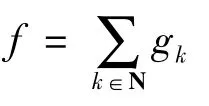
这里dk=diam(supp gk)＜∞ ，(R3)为R3中所有具有紧支集的Lp′(R3)函数构成的空间。

2018年1-9月，全省规模以上中小工业企业盈利好转。截至9月底，纳入统计的全省规模以上中小工业企业共有4153户，资产合计11660.5亿元，同比增长3.4%；主营业务收入5602.4亿元，增长20.0%；利润总额336.2亿元，同比增长6.0%；利税总额660.6亿元，增长33.9%。从业人员61.2万人，减少0.3%。

另外，在证明过程中我们需要如下插值不等式:

2 定理1的证明

本小节给出定理1的证明。不失一般性，在本小节以及下一小节，我们均假设μ=κ=1。首先，(1)的第一个方程与第二个方程两端分别乘以Δu与Δθ，并将所得方程在R3上积分，得

注意到

利用不可压条件▽·u=0，可得

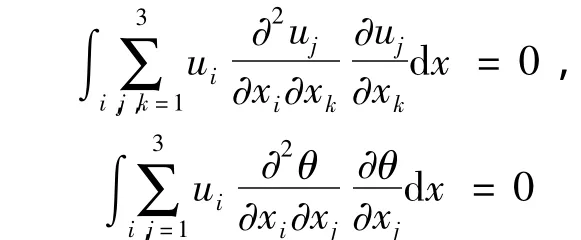
因而有

将 (5)与 (6)相加，并将 (7)－(9)代入，得

下面分两种情况来讨论:q＜+∞与q=+∞。

第一种情况:当q＜+∞时。对第一项I1应用H¨older不等式，

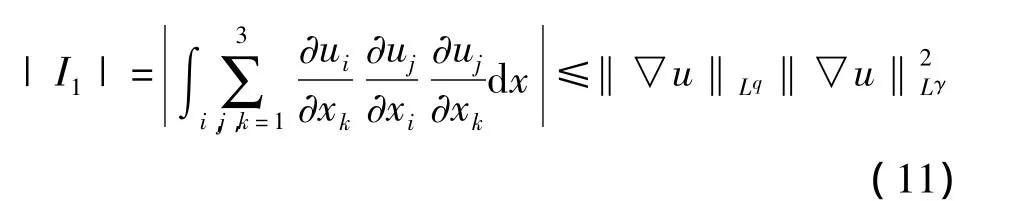
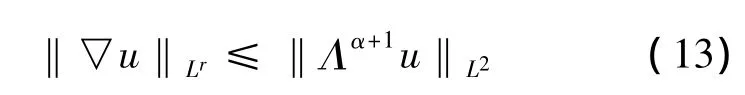
由 (11)－(13)及Young不等式，可得

根据上面证明过程可知

对于第二项I2，类似讨论可得，

其中指标σ与 (15)相同。

对于第三项I3，应用H¨older不等式及Young不等式，得

将 (14)，(16)，(17)代入 (10)，有

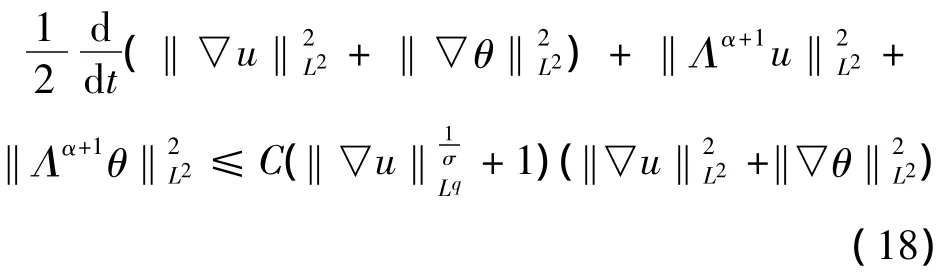
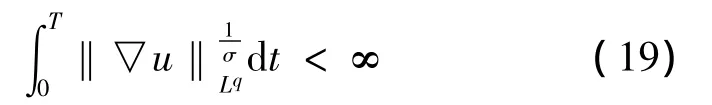
于是，对于不等式 (18)，应用Gronwall不等式可知当q＜+∞ 时，光滑解(u，θ)在时刻t=T处仍然是光滑的。

第二种情形:当q=+∞时。对式 (10)最右端第一项I1应用H¨older不等式，得

对第二项I2，应用H¨older不等式，有

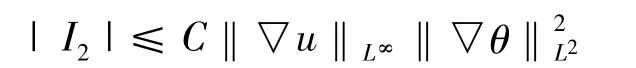
将上述不等式与式 (10)以及式 (17)联立，得

成立，则光滑解(u，θ)在时刻t=T处仍然是光滑的。定理1证毕。

3 定理2的证明

在本小节，我们给出定理2的证明。在式(10)中，对于第一项I1，应用引理1，引理2，引理3以及Young不等式，有

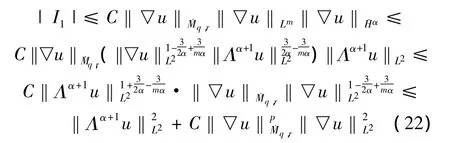
类似讨论可得，对于第二项I2，

对于第三项I3，应用H¨older不等式及Young不等式，得

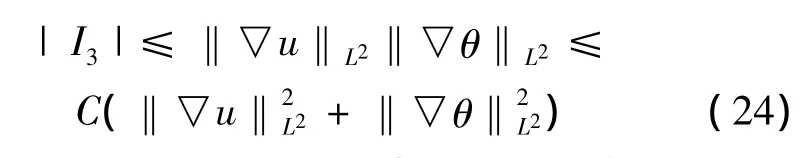
联立式 (10)，(22)，(23)与 (24)，有

对式 (25)应用 Gronwall不等式，可知在假设(4)条件下光滑解(u，θ)在时刻t=T处仍然是光滑的。定理2证毕。

［1］MAJDA A.Introduction to PDEs and waves for the atmosphere and ocean［M］.New York:Courant Lecture Notes in Mathematics，vol.9，AMS/CIMS，2003.

［2］PEDLOSKY J.Geophysical fluid dynamics［M］.New York:Springer-Verlag，1987.

［3］WU J.Regularity criteria for the generalized MHD equations［J］.Comm Partial Differential Equations，2008，33:285－306.

［4］CANNON J R，DIBENEDETTO E.The initial problem for the Boussinesq equations with data inLp［J］.Lect Notes Math，1980，771:129－144.

［5］TANIUCHI Y.A note on the blow-up criterion for the inviscid 2d Boussinesq equations［J］.Lecture Notes in Pure and Applied Mathematics，2002，223:131 －140.

［6］WEINAN E，SHU C W.Small scale structure on Boussinesq convection［J］.Phys Fluids，1994，6:48－54.

［7］CHAE D.Global regularity for the 2d Boussinesq equations with partial viscosity terms［J］.Adv Math，2006，203:497－515.

［8］HMIDI T，KERAANI S.Global well-posedness result for two-dimensional Boussinesq system with a zero diffusivity［J］.Adv Diff Equations，2007，12:461 －480.

［9］HOU T Y，LI C.Global well-posedness of the viscous Boussinesq equations ［J］.Discrete Contin Dyn Syst，2005，12:1－12.

［10］ISHIMURA N，MORIMOTO H.Remarks on the blowup criterion for the 3D Boussinesq equations［J］.Math Meth Appl Sci，1999，9:1323 －1332.

［11］QIU H，DU Y，YAO Z.Serrin-type blow-up criteria for three-dimensional Boussinesq equations［J］.Appl A-nal，2010，89:1603 －1613.

［12］XU X.Global regularity of solutions of 2d Boussinesq equations with fractional diffusion ［J］.Nonlinear Anal，2010，72:677－681.

［13］CHEMIN J Y.Perfect incompressible fluids［M］.New York:Oxford University Press，1998.

［14］LEMARIE-RIEUSSET P.Recent developments in the Navier-Stokes problem ［M］.London:Chapman and Hall/CRC，2002.

［15］BERGH J，LOFSTROM J.An introduction to interpolation［M］.Berlin:Springer，1976.