局部凸空间的中点局部k－一致*凸性与中点局部k－一致光滑性

陈利国，罗 成，王 君

(1.内蒙古财经大学统计与数学学院，内蒙古呼和浩特 010070;2.内蒙古大学数学科学学院，内蒙古呼和浩特 010021)

1977年，文献 ［1］首次给出局部凸空间严格凸的定义，并开始对局部凸空间凸性的研究，之后，文献［2］进一步研究了严格凸的条件。1989年，文献 ［3］中给出与文 ［2］中严格凸等价的定义，同时首次给出局部凸空间光滑性的定义，并建立严格凸性与光滑性的对偶关系，随后又在文献［4］中给出局部凸空间一致凸性的概念。2003年，文献 ［5］利用X上定义的一族半范数P，重新给出偶对 (X，P)的几种凸性和光滑性的定义，讨论了几种凸性 (光滑性)之间的关系，并建立重要的对偶关系。2010年，文献［6］将几种凸性和光滑性推广为k－凸性和k－光滑性［5］。但对于某些k－凸性和k－光滑性的研究却很少。主要原因是未能体现k－凸性和k－光滑性的重要对偶性质。2011年，文献 ［7］给出局部凸空间的 (弱)中点局部一致凸性，并证明它与(弱)中点局部一致光滑性是一对对偶概念［8］。本文进一步研究局部凸空间的k－凸性和k－光滑性，首先，引入局部凸空间的 (弱)中点局部k－一致凸性和 (弱)中点局部k－一致光滑性这一对对偶概念，它们既是Banach空间相应概念的严格推广［9－10］，又是局部凸空间 (弱)中点局部一致凸性和 (弱)中点局部一致光滑性的自然推广。然后，讨论它们与其它k－凸性 (k－光滑性)之间的重要关系，推广了Banach空间的某些结果。

下面是本文用到的一些预备知识和记号，以方便读者能够更快地了解本文。

下面给出本文中常用的几个符号:

对任意p∈P，令Up(X){x∈X:p(x)≤1}，Sp(X)={x∈X:p(x)=1}，即Up(X)和Sp(X)分别表示半范空间(X，p)中的单位球和单位球面;

对任意的p∈P，x1，x2，…，xk+1∈Sp(X)，记

本文所用到的其它有关概念和记号，请参见文献 ［5，7，11］。

1 相关概念

定义1［5］设B是(X，TP)中形如B{Cp}的绝对凸有界闭集，p∈P，若Cp=1，则称B是(X，TP)中的p－正规集。(容易知道若B是p－正规集，则B⊂Up(X))。

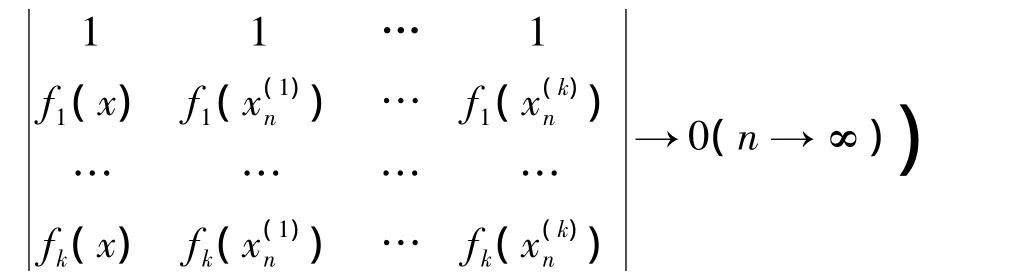
定义4［6］称偶对(X，P)为k－光滑的，若对任意p∈P，x∈Sp(X)，以及X中含有x的任一p－正规集B决定的X′上的半范数，当{f1，f2，…，fk+1}⊂∑p(x)时，有(f1，f2，…，fk+1)=0。

定义5［6］称偶对(X，P)为k－强光滑(k－非常光滑)的，若对任意的p∈P，x∈Sp(X)，以及X中含有x的任一p－正规集B决定的X′上的半范数，当⊂S(X′(p))，且满足时，有。

(对任意F1，F2，…，Fk∈S(X″())，有

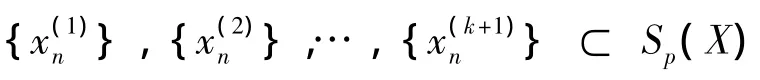
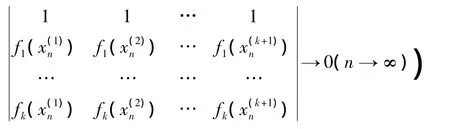
显然，中点局部k－一致凸性蕴含着弱中点局部k－一致凸性。

注1k=1时定义6就是文献 ［7］中 (弱)中点局部一致凸性。

(对任意F1，F2，…，Fk∈S(X″))，有

显然，中点局部k－一致光滑性蕴含着弱中点局部k－一致光滑性。

注3k=1时定义7就是文献 ［8］中 (弱)中点局部一致光滑性。

注4 若将P视为一范数‖·‖组成的单元素集，即(X，P)=(X，‖·‖)，定义6和定义7与文献 ［9－10］中Banach空间相应定义完全一致，也说明了本文给出的定义是Banach空间相应定义的严格推广。

2 (弱)中点局部k－一致凸性和(弱)中点局部k－一致光滑性的对偶性质

定理1(i)若偶对(X′，P*)是中点局部k－一致凸的，则偶对(X，P)是中点局部k－一致光滑的。

(ii)若偶对(X′，P*)是弱中点局部k－一致凸的，则偶对(X，P)是弱中点局部k－一致光滑的。

证明 只证 (i)，(ii)类似。

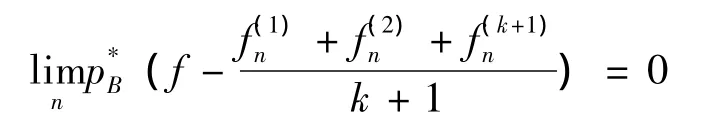
另一方面，由文献 ［12］引理2.1可知f∈(X′)。再由偶对 (X′，P*)是中点局部k－ 一致凸的。故，即偶对(X，P)是中点局部k－一致光滑的。

定理2 (i)若偶对(X′，P*)是中点局部k－一致光滑的，则偶对(X，P)是中点局部k一致凸的。

(ii)若偶对(X′，P*)是弱中点局部k－一致光滑的，则偶对(X，P)是弱中点局部k－一致凸的。

证明 只证 (i)，(ii)类似。

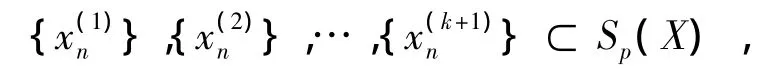
则B是X中的p－正规集且含有x和}(j=1，2，…，k+1)。

令是由B决定的X′上的半范数，则由文献［12］引理2.1可知f∈(X′)。令

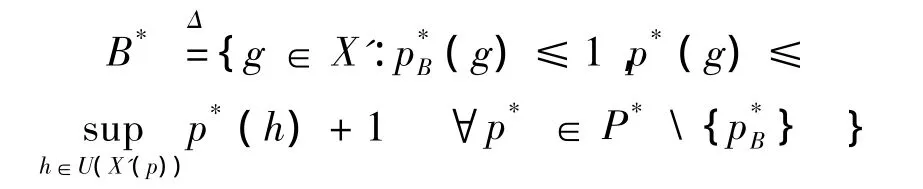
则易知B*是X′中的－正规集且含有f，且U(X′(p))⊂B*⊂(X′)。

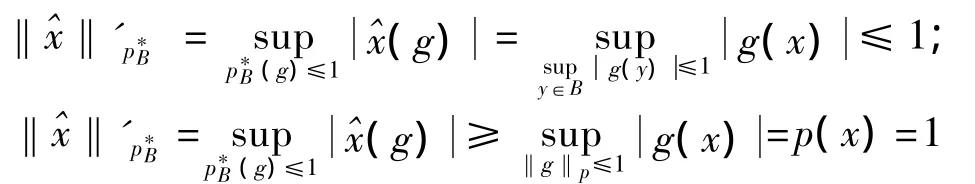
另一方面，由于^x(f)=f(x)=1，所以∈(f)。由于

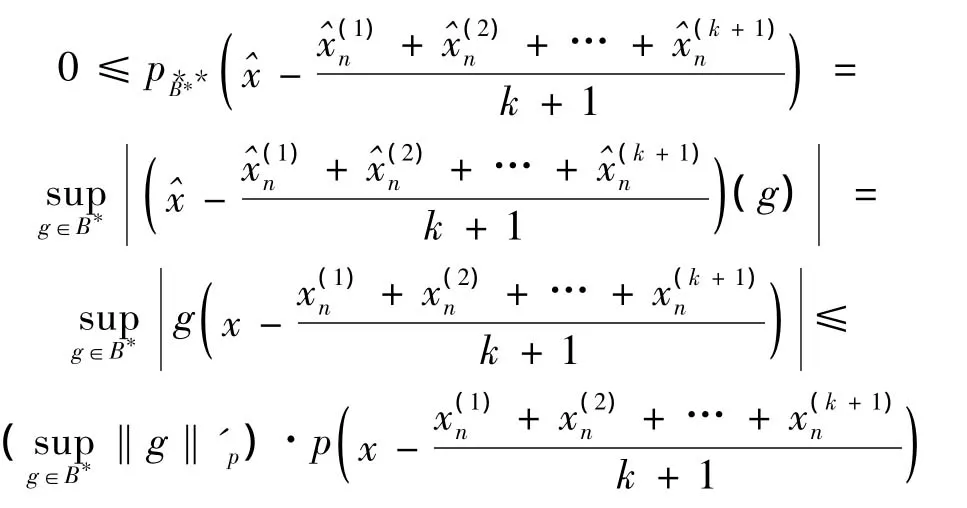
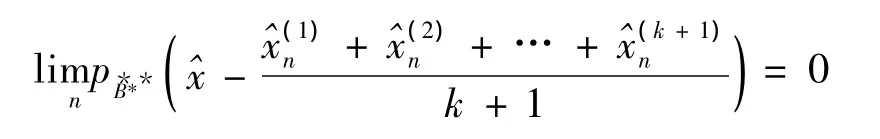
再由偶对 (X′，P)*是中点局部k－一致光滑的，类似与文献 ［13］中可以证明U(X′(p))⊂U(X‴))(在自然嵌入意义下)，故

从而证明了偶对(X，P)是中点局部k－一致凸的。

在凸性和光滑性理论的研究中，相互对偶的概念及其性质的研究占据着重要的地位。因此，合理引进并研究某种凸性 (或光滑性)的对偶概念－光滑性 (或凸性)显得尤为重要。定理1和定理2说明本文引进的局部凸空间的 (弱)中点局部k－一致凸性和 (弱)中点局部k－一致光滑性是一对对偶概念，进而说明引进的概念是合理的。

3 (弱)中点局部k－一致凸性和(弱)中点局部k－一致光滑性与其它k－凸性和k－光滑性之间的关系

下面结论是Banach空间相应结果的推广

定理3 若偶对(X，P)是k－强凸的，则偶对(X，P) 是中点局部k－一致凸的。

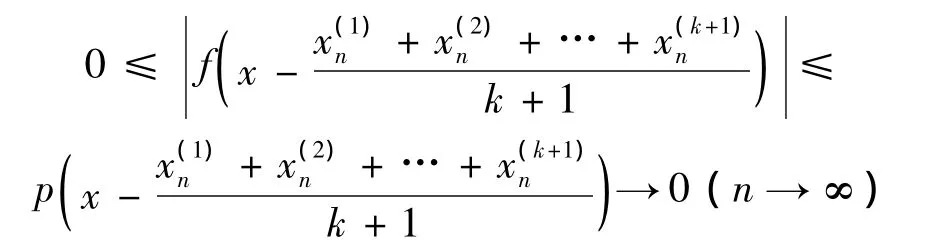
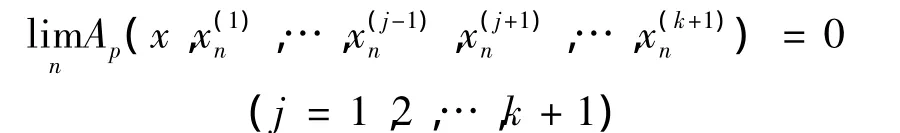
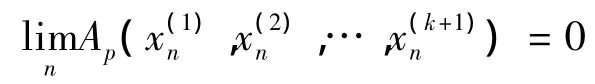
类似可以证明:

定理4若偶对X，()P是k－非常凸的，则偶对X，()P是弱中点局部k－一致凸的。

定理5若偶对X，()P是弱中点局部k－一致凸的，则偶对X，()P是k－严格凸的。

证明 对任意p∈P，当x1，x2，…，xk+1∈X，且满足

对 ∀n∈N，j=1，2，…，k+1 ，令，显然 {}(⊂Sp(X))是Tp有界序列 (j=1，2，…，k+1)。而且又由偶对(X，P)是弱中点局部k－一致凸的，所以

对任意的f1，f2，…，fk∈S(X′(p))，有

即Ap(x1，x2，…，xk+1)=0，这也就证明了偶对(X，P) 是k－严格凸的。

定理6若偶对(X，P)是k－强光滑的，则偶对(X，P)是中点局部k－一致光滑的。

证明 对任意的p∈P，x∈Sp(X) ，以及X中含x的任一p－正规集B决定的X′上的半范数，f∈ ∑p(x) ，S( X′(p) )，且。因为

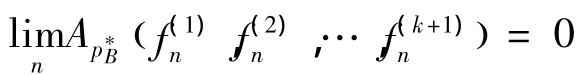
类似可以证明:

定理7若偶对(X，P)是k－非常光滑的，则偶对(X，P)是弱中点局部k－一致光滑的。

定理8若偶对(X，P)是弱中点局部k－一致光滑的，则偶对(X，P)是k－光滑的。

证明 对任意p∈P，x∈Sp(X)，以及X中含有x的任一p－正规集B决定的X′上的半范数， 且 {f1，f2，…，fk+1}⊂ ∑p(x)，令f=，则f∈∑p(x)。令，对任意n∈N=fi，显然∈S(X′(p))(i=1，2，…，k+1)，显然有由条件偶对(X，P)是弱中点局部k－一致光滑的，有Ap*B(f1，f2，…，fk+1)=0。即偶对 (X，P)是k－ 光滑的。

参考文献:

［1］DIMINNIE C R，WHITE A G.Strict convexity in topological vector spaces［J］.Math Japonica，1977，22(1):49－56.

［2］DIMINNIE C R，WHITE A G.Strict convexity conditions for seminorms［J］.Math Japonica，1980，24(5):489－495.

［3］国起，吴从炘.局部凸空间的严格凸性与光滑性［J］.东北数学，1989，5(4):465－472.

［4］吴从炘，国起.局部凸空间的一致凸性［J］.数学年刊，1990，11A(3):351－354.

［5］林敏，刘德，罗成，等.对局部凸空间凸性的探讨［J］.内蒙古大学学报:自然科学版，2003，34(5):485－489.

［6］郝建军，刘德.局部凸空间中若干种k－凸性k－光滑性的研究［J］.内蒙古大学学报:自然科学版，2010，41(1):34－40.

［7］陈利国，罗成.关于局部凸空间的中点局部一致凸性［J］.纯粹数学与应用数学，2011，27(6):749－755.

［8］陈利国，罗成.局部凸空间的几种光滑性及其等价条件［J］.集宁师专学报，2009，31(4):1－5.

［9］冼军，黎永锦.若干k－凸性的等价条件［J］.中山大学学报:自然科学版，2003，42(1):12－15.

［10］陈利国，罗成.k－非常凸、k－非常光滑与(弱)中点局部k－一致光滑空间［J］.内蒙古大学学报:自然科学版，2007，38(5):494－497.

［11］WILANSKY A.Modern methods in topological vector spaces［M］.New York:Mc GrnHill，1978.

［12］陈利国，罗成.关于局部凸空间的性质(WM)与性质(WM)*［J］.内蒙古大学学报:自然科学版，2008，39(5):499－502.

［13］陈利国，罗成.局部凸空间的k－一致极凸性与k－一致极光滑性［J］.数学的实践与认识，2011，41(20):225－232.