权值直接确定的三角型模糊前向神经网络*

杨文光

(华北科技学院基础部，北京 101601)

神经网络的研究从20世纪40年代开始，经过半个多世纪的发展，现已成为信息加工、处理、存储和搜索的重要工具［1］，在分布式存储、并行性计算、智能控制、通信等方面备受研究者的关注［2－4］。前向神经网络是目前研究最多的网络形式之一，在Rumelhart E.和Williams R.J.等为首的研究小组提出的具有强大学习和训练功能的BP学习算法作用下，使其具有了逼近任意非线性函数的能力。前向神经网络的发展与问题并存，从网络结构来讲，隐层神经元数过少将无法达到学习和逼近的效果，隐层神经元数过多又将使网络出现过拟合等不良现象，同时在硬件实现上也将难以完成。文献［5］利用逼近论对单一隐层前向神经网络进行了研究，在理论层面上阐述了神经网络的本质逼近阶既与隐层神经元个数有关，又与被逼近函数的光滑性有关;随后，曹飞龙等在文献 ［6］中使用构造法得出了单隐层神经网络逼近定义在紧集上的任意连续函数的逼近速度不超过该网络的最佳多项式逼近的二倍的结论。最近几年关于神经网络的插值性问题研究日渐增多，考虑到神经网络在全局上具有较好的逼近精度，若再解决局部结点处的插值问题则会效果更好［7－10］。文献 ［7－10］分别针对一般的Sigmoidal激励函数和一类广义激励函数，构造了精确插值和近似插值神经网络，讨论了逼近误差，这些文献从理论上给出了满足插值意义的神经网络存在性的证明，但构造非常复杂，并且缺少对应的数值仿真算例加以佐证。

前向神经网络与模糊系统的结合产生了模糊前向神经网络，使得神经元的解释变得更加合理，作为神经网络构成要素的激励函数、网络结构和学习算法也随之发生改变。张雨浓教授在函数逼近论研究基础上对BP算法做了有意义的改进，提出了隐层神经元最优权值直接确定算法，有效克服了最优权值难以确定的问题，也避免了网络过拟合和泛化问题［11－14］。插值方法作为函数逼近的简单实用工具在众多领域发挥了重要作用，对于如何有效利用蕴含重要信息的采样数据集，使其还原并丰富有限采样数据所代表的真实系统日渐成为有趣的研究课题。本文将使用模糊系统的三角型隶属函数和隐层神经元输出的乘积作为模糊前向神经网络的激励函数，依据采样数据集所含数据对个数确定隐层神经元个数，简化最优网络结构的确定过程，然后利用权值直接确定算法确定相应的最优权值，建立近似插值模糊前向神经网络，最后结合数值仿真实例突出所构建网络的有效性和实时性。

1 模糊前向神经网络结构

为明确起见，下面对一些基本术语和记号加以约定和标记。

设在二维Euclid空间，经传感器采样获得m组采样数据，分别为(x1，y1)，(x2，y2)，…，(xm，ym)，亦即插值样本，同时将这m组采样数据作为网络的训练数据。依据采样数据的重要性对m组采样数据进行遴选获得n组较为重要的具有代表性的数 据， 记 作 (x′1，y′1)，(x′2，y′2)，…，(x′n，y′n)，称为构造数据，作为生成隐层神经元的母体，故n≤m，在网络建立过程中所采用的构造数据集就是训练数据集 (插值样本集)的子集。现在构造与采样数据维数相符的包含单一隐层的单输入单输出前向神经网络

其中x∈R为输入变量，n为隐层神经元个数，c=(c1，c2，…，cn)T是输入层神经元与隐层神经元之间的连接权值向量，w=(w1，w2，…，wn)T是隐层神经元与输出层神经元之间的连接权值向量，σ是隐层神经元激励函数，θi是隐层神经元阈值 (i=1，2，…，n)。

定义1 对于插值样本 (x1，y1)，(x2，y2)，…，(xm，ym)，若公式⑴满足插值条件f(xi)=yi，则称f(x)是采样数据的精确插值神经网络;若f(xi)≈yi，则称f(x)是采样数据的近似插值神经网络 (i=1，2，…，m)。

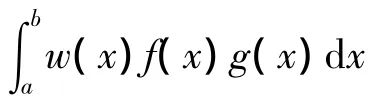
定理1［15］求解定义2中的s*∈Φ，等价于求解多元函数

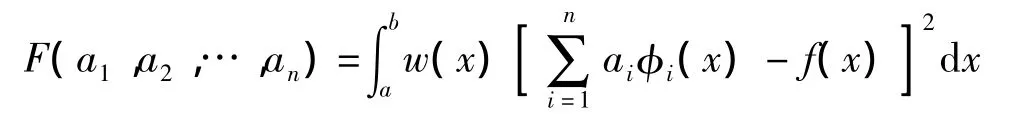
在前向神经网络⑴基础上，选择σ为三角型隶属函数与构造数据的组合，充分体现相应神经元的激活程度，假设c=(c1，c2，…，cn)T=(1，1，…，1)T，θi=0(i=1，2，…，n)，以简化计算，使用构造数据中的每组数据作为母体构造隐层神经元，组成隐层含n个神经元的单输入单输出模糊前向神经网络

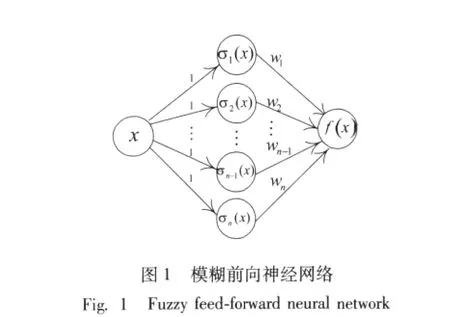
单输入单输出系统的模糊前向神经网络的结构见图1。现对(2)式中三角型隶属函数加以说明，由构造数据提取出第一维数据得到X=(x′1，x′2，…，x′n)，提 取 第 二 维 数 据 得 到Y=(y′1，y′2，…，y′n)，在模糊系统的构造中，通常以 (x′1，x′2，…，x′n)为峰点构造全交叠三角型模糊集，其图形见图2。

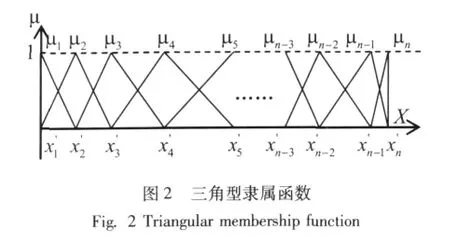
使用编程易于实现的表示法对图2所示三角型模糊集描述为:

当x′i≤x≤x′i+1时，模糊集 μi和 μi+1的隶属度分别为 μi(x)=(x′i+1－x)/(x′i+1－x′i)，μi+1(x)=(x－x′i)/(x′i+1－x′i);相应神经元激励函数为σi(x)=μi(x)y′i，σi+1(x)=μi+1(x)y′i+1就表示对应神经元输出的激活程度大小 (i=1，2，…，n－1)。

显然，μ1(x)，μ2(x)，…，μn(x)∈L2w［x′1，x′n］，则 σ1(x)，σ2(x)，…，σn(x)∈L2w［x′1，x′n］，且线性无关，故由定理1可知存在模糊前向神经网络f(x)可以最佳平方逼近插值样本集所代表的系统。

2 权值直接确定算法

采样数据蕴含着未知系统内部的函数关系，前面使用构造数据所建立的单输入单输出的模糊前向神经网络，还需要进一步使用训练数据进行训练，使其达到更高的逼近精度。

定义3 设实矩阵V∈Rn×m，如果U∈Rm×n，满足VUV=V，UVU=U，(VU)T=VU，(UV)T=UV，则称U为V的Moore-Penrose广义逆矩阵或伪逆。

依据张雨浓教授所提出的前向神经网络权值直接确定算法［12－14］，对于单输入单输出模糊前向神经网络，由误差反向传播学习算法亦可得如下定理。

定理2 模糊前向神经网络⑵在训练数据(x1，y1)，(x2，y2)，…，(xm，ym)作用下，得输入受激励矩阵U∈Rm×n，设 α=(x1，x2，…，xm)T∈Rm，β=(y1，y2，…，ym)T∈Rm，令w表示模糊前向神经网络的最优权值向量，则有

其中，代入α得

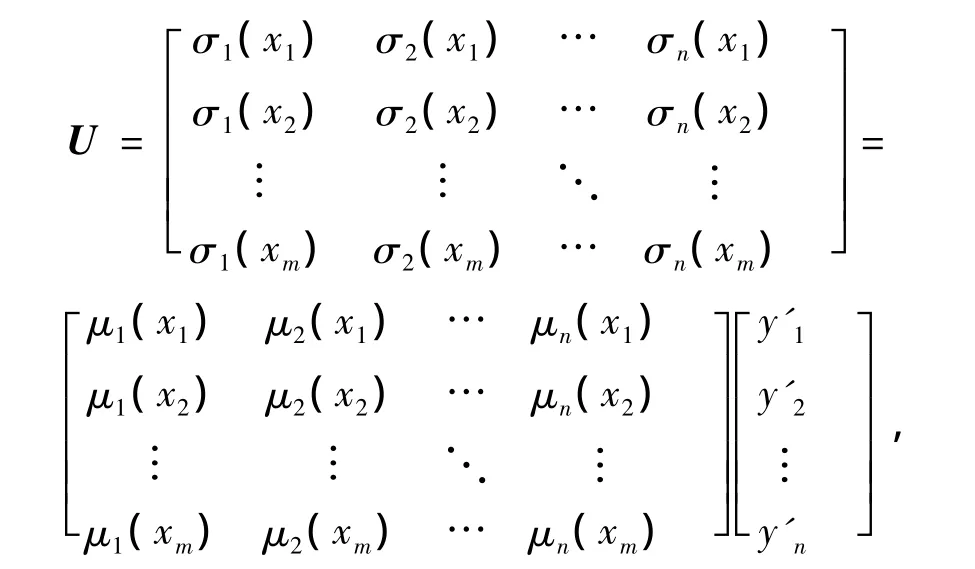
(UTU)－1UT是输入受激励矩阵U的广义逆矩阵(伪逆)，在MATLAB软件中可直接调用函数pinv(U)求解。

证明 由矩阵论知识可知，对于矩阵方程组Uw=β，只有U是列满秩时，最小二乘解才是唯一的，且为(UTU)－1UT，否则便有无穷多最小二乘解。

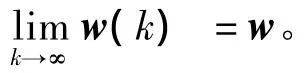
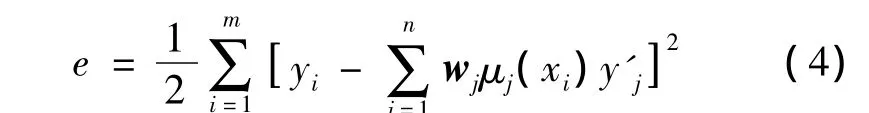
由BP算法负梯度思想可知

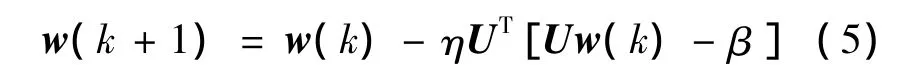
对 (5)式两边取极限，即为所求，其中学习率η取1。证毕。

定理3 模糊前向神经网络 (2)是近似插值神经网络。

证明 对于采样数据即训练数据 (x1，y1)，(x2，y2)，…，(xm，ym)和 构 造 数 据 (x′1，y′1)，(x′2，y′2)，…，(x′n，y′n)而言，构造数据用于构造隐层神经元隶属函数确定网络结构，而训练数据则用于训练网络，在权值直接确定算法作用下得到网络的最优权值向量w。

对于任意输入x，当x=xi时，i=1，2，…，m，将式(2)展开为矩阵形式得

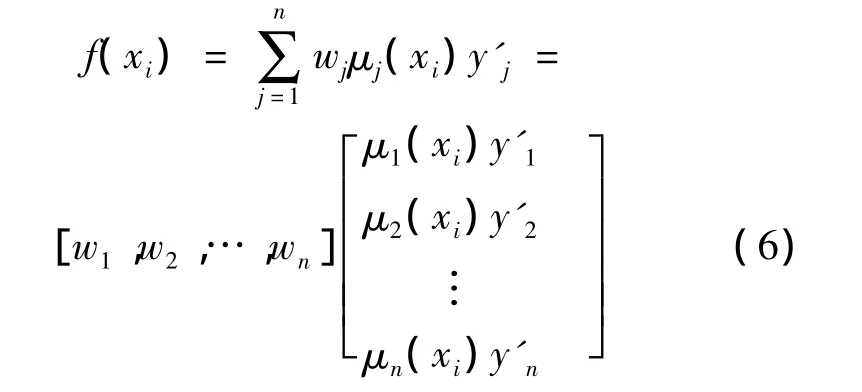
第一种情况:若xi∈X，则存在唯一的非零模糊集μj，使得μj(xi)=1，由此可得f(xi)=wjy′j，此时y′j=yi;

第二种情况:若x∉X，则有且只有两个非零模糊集μj和μj+1，使得μj(xi)＞0，μj+1(xi)＞0，且μj(xi)+μj+1(xi)=1，简化⑹式得f(xi)=wjμj(xi)y′j+wj+1μj+1(xi)y′j+1，i=1，2，…，m，j=1，2，…，n－1。

无论是哪种情况，均由定理2的推导可知最优权值向量w是在保证最佳平方逼近下得到的，故f(xi)≈yi，模糊前向神经网络(2)是近似插值神经网络，i=1，2，…，m，j=1，2，…，n－1。证毕。

3 数值仿真实例

本节将在基于采样数据和构造数据构建的模糊前向神经网络的基础上，选用张雨浓教授在文献［13］中所使用的 4个目标函数，在 MATLAB 7.5.0(R2007b)中进行数值仿真实验，以加强对比说明的效果。在工程实践中，测量误差是无法消除的，当逼近精度达到一定的有效位数后，实时性的要求变的更为重要。所选用的4个目标函数依次为:φ1(x)=ex+x2+cos 3.6πx，φ2(x)=excos 2πx，φ3(x)=sin 8x/cosx，φ4(x)=x7/ex+sin 10x。

首先提取训练数据和构造数据，选择 ［–1，0.8］为训练区间，按照前面隐层神经元建立方法，以h1=0.01 s为采样步长，得181组训练数据，即m=181;假设按照重要性对训练数据进行等间隔提取构造数据，提取步长h2=0.02 s，即n=91，亦即隐层神经元个数，在此选择的步长遵循前面的要求，即h1≤h2，m≥n。模糊前向神经网络的逼近精度随构造数据的增多而提高，直到选择的隐层神经元个数n=m为止，达到最好的逼近效果，具体仿真结果见图3中的 (a)-(d)。模糊前向神经网络的逼近效果取决于采样数据的多少，采样数据越多，构造数据的选择亦可增多，在表1中，将会给出具体的参数指标，如网络运行时间，均方差，以及改变构造数据步长h2发生的相应改变。

图3 模糊前向神经网络的逼近Fig.3 The approximation of fuzzy feed-forward neural network

表1 模糊前向神经网络仿真结果Table 1 The results of fuzzy feed-forward neural network's simulation

从图3和表1，不难发现，各个目标函数的运行时间均减少到参考文献 ［13］的1%左右，在隐层神经元个数为采样数据个数一半的情况下就已经达到了很高的逼近精度，当选用全部采样数据用于构造隐层神经元时，则达到了10－33次的数量等级的逼近精度，误差基本可以忽略不计。下面进一步说明本文所构建的网络具有较好的预测性能。同样，选择区间 ［–1，0.8］为预测区间，选择目标函数1和2，给出真实模型，选择h1=h2=0.01 s，得到模糊前向神经网络模型⑵，然后使用rand()函数在区间 ［–1，0.8］上随机生成360个数作为输入送入到模糊前向神经网络模型⑵中，得到预测输出，见图4中的 (a)-(b)。表2给出了与图4相应的运行时间、预测数据的均方差等性能指标参数，表明预测精度很高。

图4 模糊前向神经网络的预测Fig.4 The predication of fuzzy feed-forward neural network

表2 模糊前向神经网络预测结果Table 2 The results of fuzzy feed-forward neural network's predication

4 结论

本文避开了前向神经网络建立时所遵循的复杂的网络结构和学习算法的迭代学习过程，得到了基于采样数据建立的模糊前向神经网络，该网络为实时还原真实系统提供了有效解决方法。该网络能够根据采样数据的多少实现隐层神经元的自主设定，并且利用权值直接确定算法直接确定了最优权值，缩短了网络运行时间，相应的网络运行时间都在毫秒级。计算机数值仿真实验表明，基于三角型隶属函数建立的模糊前向神经网络是一种具有较高逼近精度和预测精度的实时性神经网络，在工程实践中将会具有很好的借鉴意义。

［1］李士勇.模糊控制·神经网络和智能控制论［M］.哈尔滨:哈尔滨工业大学出版社，1998.

［2］张雨浓，张禹珩，陈轲，等.线性矩阵方程的梯度法神经网络求解及其仿真验证［J］.中山大学学报:自然科学版，2008，47(3):26－32.

［3］陈北京，孙星明，王定成，等.基于彩色图像四元数表示的彩色人脸识别［J］.自动化学报，2012，38(11):1815－1823.

［4］张文辉，叶晓平.参数突变自由漂浮空间机器人神经集成控制［J］.中国科学:信息科学，2012，42(11):1435－1444.

［5］曹飞龙，徐宗本.神经网络的本质逼近阶［J］.中国科学:E辑，2004，34(4):361－373.

［6］曹飞龙，张永全，张卫国.单隐层神经网络与最佳多项式逼近［J］.数学学报:中文版，2007，50(2):385－392.

［7］LIANAS B，SAINZ F J.Constructive approximate interpolation by neural networks［J］.J Comput Applied Math，2006，188:283－308.

［8］谢庭藩，曹飞龙.关于插值神经网络的构造性［J］.自然科学进展，2008，18(3):334 －340.

［9］徐士英，曹飞龙.距离空间中插值神经网络的误差估计［J］.系统科学与数学，2009，29(5):670－676.

［10］徐士英，曹飞龙.多元插值神经网络的一个注记［J］.高校应用数学学报，2009，24(1):91－94.

［11］张雨浓，谭宁，李展，等.求解线性不定方程组所展现的BP与Hopfield类型神经网络的学习同质性研究［J］.中山大学学报:自然科学版，2010，49(2):1 －7.

［12］张雨浓，李凌峰，郭东生，等.Hermite插值神经网络权值和结构确定理论探讨［J］.计算机应用研究，2010，27(11):4048 －4051.

［13］张雨浓，郭东生，谭宁.幂激励前向神经网络最优结构确定算法［J］.计算机工程与应用，2011，47(2):29－31.

［14］肖秀春，张雨浓，姜孝华.MISO多元广义多项式神经网络及其权值直接求解［J］.中山大学学报:自然科学版，2009，48(4):42 －46.

［15］薛毅.数值分析与科学计算［M］.北京:科学出版社，2011.