二进制张量分解法简化神经网络推理计算①
郝一帆 杜子东 支天
(∗中国科学院计算技术研究所智能处理器研究中心 北京100190)
(∗∗中国科学院大学 北京100049)
0 引言
近年来,智能驾驶、智慧医疗、大数据金融系统等多个领域逐步掀起了深度学习的热潮。作为深度学习中最具代表性的算法模型,人工神经网络是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。人工神经网络中包含大量的参数以及乘积累加运算(multiply-accumulate,MAC),并且人工神经网络的计算量随参数量呈逐年显著上升趋势。1998 年,用于手写字符识别的神经网络规模小于1 ×106个参数[1]。2012 年,用于参加ImageNet 竞赛的模型规模约6 × 107个参数[2]。2018 年,自然语言处理模型BERT 含有约3×108个参数,以及数十亿的MAC 运算。人工神经网络作为最主要的深度学习模型,其逐年增长的计算量为计算系统带来了巨大的负载,从而限制了深度学习在移动端设备的应用。所以,对神经网络模型进行简化是研究者们面临的一个重大挑战。
由于神经网络执行推理计算时涉及大量耗时耗能的MAC 运算,所以减少MAC 运算中的乘法和加法操作数是简化神经网络模型的核心思路。现有的方法根据对权值数据的操作可分为两大类,即微调法与重训练法。微调法是从MAC 的计算流程入手,通过权值的低秩分解等手段配合对权值的重训练,以更少的乘加操作数完成原本的MAC 计算并得到近似的结果,例如奇异值分解(singular-value decomposition,SVD)、正则多元分解(canonical polyadic,CP)和双聚类近似等[3]。重训练法是从模型的参数本身入手,通过稀疏、量化等手段,使权值在模型重训练过程中收敛到更多的零值和更低位宽的非零值,从而使参与计算的有效数据量降低,以达到减少操作数的目的。稀疏是减少神经网络模型中非零权值数量的方法,例如迭代剪枝法[4]将小于阈值的权值归零、权值聚类法[5]减少权值的非零取值、粗粒度稀疏法[6]减轻非零权值分布的不规则程度。量化是将模型中的非零权值用更低位宽的数据取代的方法。许多工作都已经表明,对于常用的神经网络模型,可以将权值数据量化为低位宽定点数,例如8 比特,而不影响模型整体准确率[7-14]。此外,神经网络中不同层的权值数据可量化为不同位宽的定点数[15];对于某些特定的神经网络模型,甚至允许将权值量化为2 比特或1 比特[16-17]。
然而这些方法都涉及对权值的更改,无法避免执行神经网络的训练过程。所以在使用简化后的模型执行推理之前,系统需要承受模型反复训练带来的开销;在训练完毕之后,模型整体的准确度往往会有一定程度的下降。不仅如此,微调法往往面临超参难以选取的问题,例如当SVD 等低秩分解方法的秩只能通过反复实验寻找最优解。对于重训练法,量化后的不同位宽的权值对中央处理器(central processing unit,CPU)或图形处理器(graphics processing unit,GPU)中固定位宽乘法器的硬件利用率不高,这也十分不利于神经网络模型推理计算的效率。
受Stripes[18]和Laconic[19]等工作中将权值中零比特位过滤的启发,不同于此前的数据级简化方法,即将单个权值数据作为最小优化单元,本文将权值中的每个比特看作独立的数据,发现多个卷积核之间由于权值比特位重复会导致一定的计算重复。基于此,本文提出一种在比特级降低神经网络中MAC计算的乘加操作数的二进制张量分解法(identical binary tensor factorization,IBTF)以消除上述计算重复。具体地,IBTF 将权值矩阵看作0-1 二进制张量,并对该张量进行全等分解,而非近似。故IBTF不需要对权值的实际数值进行更改,也不会修改计算结果。进而IBTF 既不会有训练模型带来的额外开销,也不会对模型整体准确度造成任何损失。此外,在比特级简化MAC 计算是一种全新的优化维度,与权值低秩分解、稀疏、量化等数据级方法正交。所以IBTF 可与之前的方法结合使用,从而进一步地减少神经网络模型中MAC 运算的乘加操作数。实验结果表明,在多个主流神经网络中,相较于量化与稀疏后的模型,IBTF 进一步使计算量减少了3.32倍,并且IBTF 在不同卷积核大小、不同权值位宽、不同稀疏率的卷积运算中都发挥了显著的效果。
1 神经网络中的MAC 运算
本节主要介绍MAC 运算在神经网络推理计算中的时间占比,并基于对MAC 运算的观察,分析卷积中权值比特位重复带来的计算重复。
1.1 MAC 计算时间占比
在NVIDIA V100 GPU 上,基于深度学习框架Caffe[20],利用time 功能测得多个常用神经网络模型推理计算中各阶段的执行时间,得到结果如图1所示。在LeNet[1]、AlexNet[21]和VGG-16[22]中,卷积层CONV 和全连接层FC 的执行时间占总推理时间的80%以上,其中在卷积规模较大的VGG-16 中更是达到了94.42%。在ResNet-18[23]和ResNet-50[23]中,卷积层和全连接层的时间占比略有下降,但仍超过60%。下降的原因是这两个网络模型中的BatchNorm 层和Scale 层的逐元素乘加计算也占用了一定的时间。总之,由于卷积层与全连接层占神经网络推理计算时间的主要部分,并且在卷积层与全连接层中,除激活外全部是MAC 运算,所以简化MAC 运算有助于提升模型整体推理计算的性能。
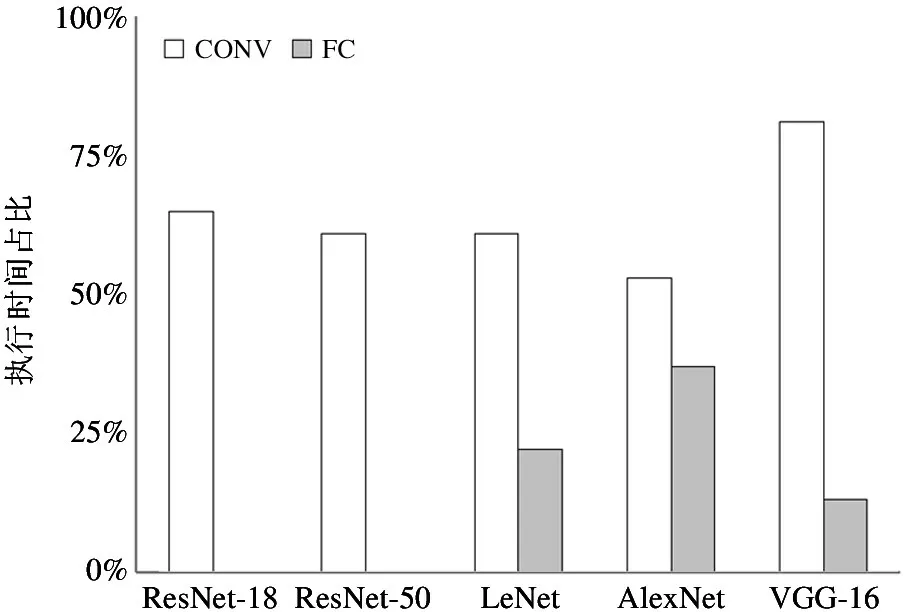
图1 常用神经网络模型中卷积层CONV 和全连接层FC 的计算时间占比
1.2 MAC 中比特位重复带来的无效计算
在卷积层和全连接层的卷积运算中,单个卷积核在每个滑动窗口的运算是一个内积操作。如图2所示,以权值量化为4 比特且大小为2 ×2 的1 个卷积核为例,4 个互不相等的非零权值分别为‘b1110,‘b1010,‘b1011,‘b0111,故不能通过稀疏(跳过零权值的计算)或合并同类项(合并相等权值的乘加)的方法减少操作数,即该卷积运算在数据级已无任何可简化的空间。但是只要细化到比特级,即将权值数据的每个比特单独考虑,按照竖式加法将整个内积运算拆开后,可以观察到单个卷积核的MAC 运算中含有两种无效计算:一种是由单个权值中的零比特位带来的含零加法,在图中由虚线框标出;另一种是由不同权值间的相同比特位带来的重复加法,在图中由实线框标出。于是,对于稀疏和合并同类项等数据级简化算法无效的该示例,比特级的简化可通过消除上述两种无效计算进一步减少MAC 计算量。对于图中示例,原本需要4 个乘法操作和3个加法操作的MAC 运算,在去除上述两种无效计算后只需8 个加法操作。这一简化效果十分显著,对于普通的CPU 与GPU,一般只含有16/32/64 比特乘法器,故一个乘法的开销相当于数十个加法;即使对于含有4 比特乘法器的专用硬件,由于1 个4 比特乘法由4 个4 比特数据移位累加完成,故1 个乘法的开销约等于3 个加法。所以在图2 所示的例子中,在比特级去除无效计算后,该内积的计算开销(一个乘法的开销按上述方法根据数据位宽换算成多个加法)至少可节省为原计算开销的一半,甚至在普通CPU 或GPU 中节省数十倍。

图2 单个卷积核内的MAC 运算中的2 种无效计算示例
同理,多个卷积核在每个滑动窗口的运算是一个矩阵乘向量(matrix-vector multiply,MVM)操作。如图3 所示,以权值量化为2 比特且大小为2 ×2 的2 个卷积核kernel0、kernel1 为例,分析其中的MAC计算。同样的,此时仍逐比特考虑权值数据,并且将全部卷积核参与的计算视作一个整体(即MVM 操作),无效计算可由多个卷积核之间的权值比特位重复和零比特位带来。上述两种无效计算同样在图3 中分别由实线框和虚线框标出。于是,比特级的简化可通过消除上述两种无效计算减少MAC 计算量。对于图中示例,原本需要8 个乘法操作和6 个加法操作的MAC 运算,在去除上述2 种无效计算后只需6 个加法操作。即使对于含有2 比特乘法器的专用硬件,由于1 个2 比特乘法由2 个2 比特数据移位相加完成,故1 个乘法的开销约等于1 个加法。所以在图3 所示的例子中,在比特级去除无效计算后,该内积的计算开销(乘法的开销按上述方法根据数据位宽换算成加法)至少可节省为原计算开销的42.86%,甚至在普通CPU 或GPU 中节省数十倍。
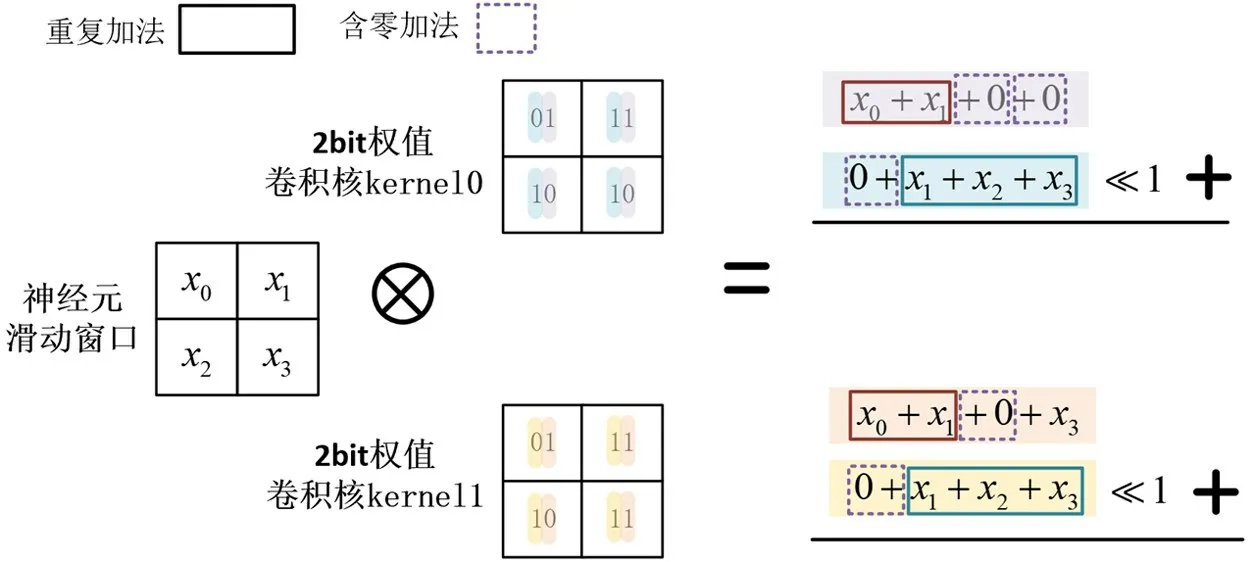
图3 多个卷积核间的MAC 运算中的2 种无效计算示例
在一般的神经网络模型中,一个卷积的计算规模远超图2 和图3 的示例。由于计算规模越大,分别由权值比特位重复和零比特位带来的2 种无效计算越频繁出现,故比特级简化减少的MAC 计算量越多,效果也越显著。于是,逐比特考虑权值数据并在比特级简化卷积计算是必要的。然而,虽然消除权值零比特位带来的无效计算可通过直接跳过零数据达成,但是提取权值比特位重复带来的无效计算的方法并不直观,原因在于权值比特位重复不仅发生在单个卷积核内,也发生在多个卷积核之间。这是本文提出IBTF 算法的动机所在。
2 IBTF 算法
本节介绍一种在卷积运算中提取权值比特位重复的算法IBTF,并说明其减少MAC 运算中的乘加操作数的显著效果。
2.1 IBTF 算法步骤
以4 比特神经网络中的某卷积层为例,设该层有6 个尺寸为16 ×4 ×4(16 个channel,kernel 大小为4 ×4)的卷积核。于是每个卷积核的单次滑动窗口内有16 ×4 ×4=256 个神经元。
第1 步,将权值逐比特展开并等效为0-1 二进制张量T。如1.2 节所述,由于单个卷积核在每个滑动窗口位置的运算是一个内积,故可将神经元和单个卷积核看作长度为256 的向量。进一步地,将6 个4 比特卷积核逐比特展开为0-1 二进制权值张量T,张量T的维度为256 ×6 ×4。
第2 步,切分0-1 二进制权值张量T。在此例中,以3 比特为切分单元,挖掘权值张量T中非零比特重复带来的无效计算。如图4 所示,首先将T划分为8 个大小为256 ×3 的0-1 二进制矩阵T1,T2,…,T8,图4(a)显示的是拆分张量T的3D 示意图,图4(b)显示的是拆分俯视图。将长度为256 的神经元向量记作x,于是整个卷积运算的结果满足式(1)。

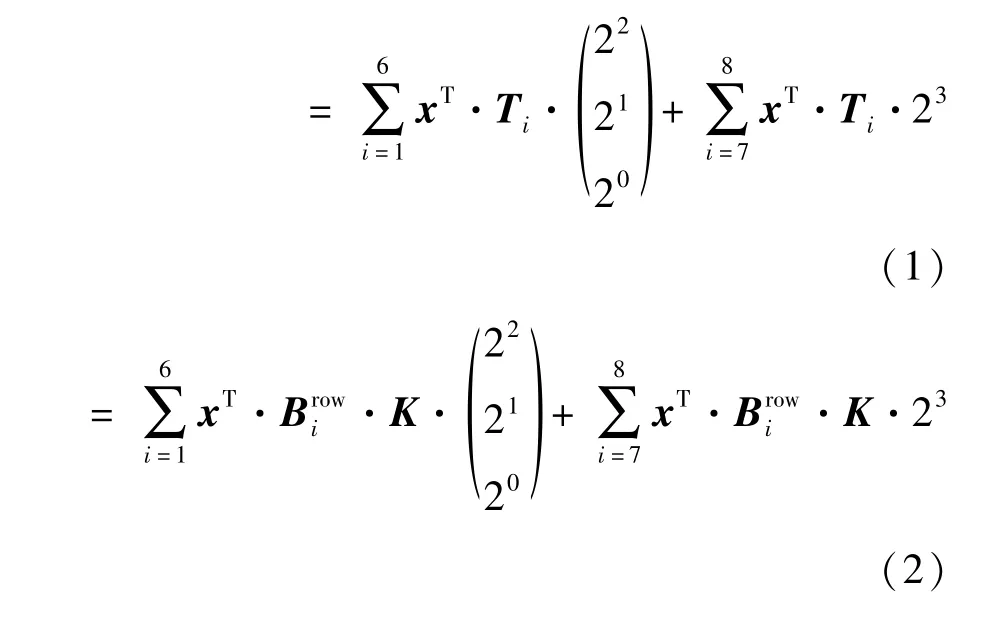
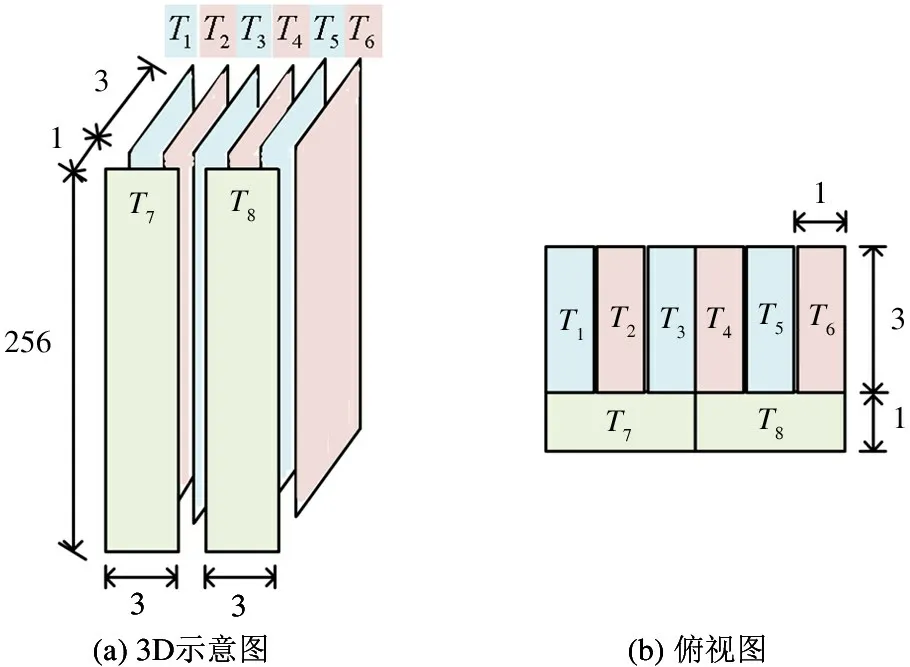
图4 IBTF 算法中的二进制权值张量切分
第3 步,对划分权值张量T后得到的二进制权值矩阵分别进行全等矩阵分解。将每个Ti(i=1,2,…,8) 分解成一个稀疏的二进制矩阵和一个非稀疏的二进制矩阵K。具体地,如图5 所示,对于大小为256 ×3 的二进制矩阵Ti,将其每行的3 比特看作一个切分单元,则该切分单元共有23-1=7种非零取值。矩阵K的每一行对应一种3 比特切分单元的非零取值,则K的大小固定为7 ×3。由于矩阵Ti的每一行的取值可从矩阵K的某一行中选出,或是取零向量,故可得到大小为1024 ×7 的稀疏矩阵,使得。其中,的每一行是一个one-hot 向量或零向量,对应Ti中一行的取值。分解完毕后,整个卷积运算的结果可写成式(2)。由于神经元与2 的次幂相乘可以由移位操作代替,与0/1 相乘可以由AND/OR 操作代替,所以由式(2)计算的卷积结果不需要任何乘法。至此,IBTF 算法完成。

图5 IBTF 算法中单个二进制权值矩阵的全等分解
2.2 IBTF 效果分析
IBTF 处理后的卷积运算并不改变运算结果,且不需要任何乘法操作,所以只需分析加法操作数就能确定IBTF 处理后的计算量。设某卷积运算中,卷积核的大小为N,个数为M,权值数据的位宽为p。于是对于该卷积操作的一个滑动窗口中,神经元可展开成长度为N的向量x,卷积核可按权值逐比特展开成大小为N × M × p的二进制张量T。设对T的切分单元大小为a,于是T可被切分为个二进制权值矩阵Ti,i=1,2,…,。而后每个Ti分解得到矩阵和K,两个矩阵的大小分别为=N ×(2a -1) 和dim(K)=(2a -1)×K。假设该卷积运算中权值的稀疏率为λ(0 ≤λ <1),于是中含有(1-λ)N个非零行向量。此时对于式(2),神经元向量x与相乘需要(1-λ)N -2a个加法,此后再与K相乘需要约2a+1个加法。于是根据式(2)计算单次滑动窗口内的卷积结果所需的总加法操作数最多为

对于2.1 节中的示例,根据卷积规模设置可知N=256,M=6,p=4,a=3。假设λ=0,即所有权值都参与MAC 运算,代入式(3)可得,经IBTF处理后,加法操作数最多为2112 个,且无任何乘法操作。而原本的卷积运算需要(1-λ)NM=1536个乘法操作与1536 个加法操作。为了更清晰地对比IBTF 简化前后的运算量,可根据数据位宽将一个乘法等效为多个加法,并将等效后的总操作数记作等效MAC 操作数Eq_MAC_op。如1.2 节所述,在实际硬件中,p比特数据的乘法由多次移位操作与至少p -1 次加法完成,故可将1个p比特乘法近似等效为p -1 个加法。于是,原本卷积运算的等效MAC 操作数为1536+1536×(4-1)=6144,是IBTF 简化后的2.91 倍。值得注意的是,在后续的实验中使用Eq_MAC_op度量运算量时,并不会将零权值参与的加法与乘法统计在内,只是在本示例中已经假设权值的稀疏率λ为0。综上,IBTF 通过提取权值比特位重复带来的无效计算,大幅减少了MAC 运算量,并且保持数值计算结果不变,从而在提升系统能效的同时不会对模型精度产生任何影响。不仅如此,由于IBTF 简化后的卷积计算不含乘法,所以也不存在不同位宽的权值对固定位宽的乘法器利用率低下的问题。
此外,在实际使用IBTF 执行神经网络推理计算时,由于权值已训练完毕并固定,所以IBTF 的运算流也是固定的。于是可以通过直接存储矩阵和K的方式代替存储权值。下面分析这种权值存储方式的开销。对于矩阵K,由于K的取值只与切分单元的大小a有关,所以只需存储a即可,即矩阵K几乎不占用任何存储。对于矩阵,由于是一个每行为全0 或只有一个1 的极度稀疏矩阵,所以可按如下方案存储:对于非零权值稠密的卷积,即中全0 的行向量较少时,只需存储记录每行中1 的位置将其按行存储;对于权值稀疏的卷积,即中全0 的行向量较多时,可通过游程编码按列存储。综上,使用IBTF 算法几乎不会带来额外的权值访存开销。
2.3 IBTF 最优切分
如式(3)所示,对于给定规模的卷积计算,经IBTF 简化后所需的加法操作数至多为[(1-λ)N+2a]·,其中N为卷积核大小,M为卷积核数量,p为权值数据位宽,λ为权值稀疏率,a为切分单元大小。由此可知,对于固定权值规模与数值的卷积计算,上述操作数仅与切分单元大小a的选取相关。于是,求使IBTF 操作数最少的切分单元问题可表达为式(4)。IBTF_op(a)对a求导可得:当a满足式(5)时,IBTF_op(a=a∗) 取最小值。综上,在给定卷积运算规模和权值数据位宽时,可以根据式(5)直接计算得到最优IBTF 拆分单元大小a∗。
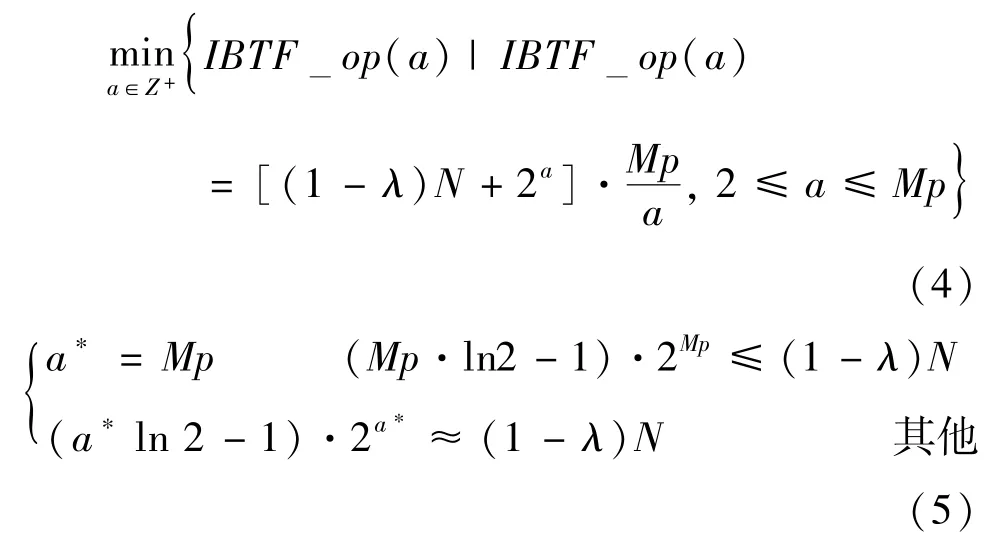
对于2.1 节的示例,根据式(5)求得最优切分单元的大小为a∗=6,此时对二进制权值张量的划分如图6 所示,并求得IBTF 的加法操作数至多为1280。相较于2.1 节示例中a=3 的切分方式,最优切分IBTF 的加法操作数进一步减少了39.4%。更具体地,图7 显示了该示例中取不同切分单元大小的操作数对比。从图中可以看出,切分单元大小的选取显著影响IBTF 的效果,于是根据式(5)求IBTF 最优切分单元大小是必要且正确的。

图6 IBTF 算法示例二进制权值张量最优切分
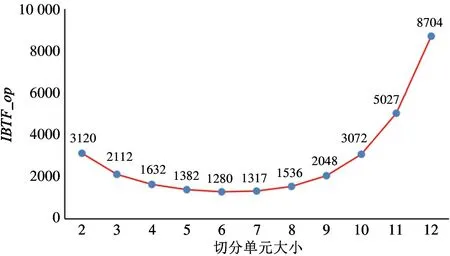
图7 IBTF 算法示例操作数与切分单元大小
3 实验
3.1 实验方法
在NVIDIA V100 GPU 上,对于不同规模、不同位宽、不同权值稀疏度的单个卷积层以及常用神经网络模型,分别执行推理计算。其中在卷积运算中,IBTF 算法对MAC 计算的简化处理类似一个即插即用(plug-and-play,PnP)模块。实验分别统计了IBTF简化后模型与原始模型的乘加操作数,以体现IBTF对MAC 计算量的简化效果。
3.2 常用神经网络中的总操作数
实验使用了一组常用的神经网络模型为测试用例集,包括AlexNet[21]、VGG-11[22]、VGG-16[22]、Res-Net-18[23]、ResNet-50[23]和GoogleNet[24],且它们执行的推理计算是在数据集ILSVRC12[25]上进行图像分类。在模型正确率下降1%以内的限制下,这些模型都可以将权值量化为8 比特以内的定点数。具体地,量化后模型的对应权值位宽[9,26-27]如表1 所示。

表1 常见神经网络模型及量化后权值位宽
如图8 所示,实验比较了稀疏(Spar.)、量化+稀疏(Quan.+Spar.)和量化+稀疏+IBTF(IBTF)处理后模型的相对计算量。其中模型的MAC 计算量可由2.2 节中所述的等效MAC 操作数Eq_MAC_op统一度量,即将每个p比特乘法等效为p -1个加法后的加法操作数。为了使图8 更清晰地显示比较结果,将量化+稀疏+IBTF 处理后每个模型的Eq_MAC_op都记为单位1(实际上不同模型的计算量并不相同),故图中纵坐标表示的是上述3 种方法相较于IBTF的相对Eq_MAC_op。实验结果显示,相较于Spar.,IBTF平均使计算量减少了11.54倍;相较于Quan.+Spar.,IBTF 平均使计算量减少了3.32倍。尤其是对于权值位宽较大(7比特)的VGG-11 网络,相较于Quan.+Spar.,IBTF平均使计算量减少了5.22 倍。综上,基于量化与稀疏简化后的模型,保持计算结果不变的IBTF 算法仍可进一步大幅减少MAC 计算量。
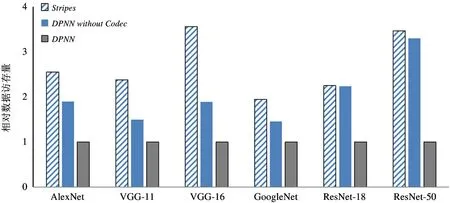
图8 常见神经网络模型在不同简化方法下的相对计算量
3.3 单个卷积层中的操作数
在上一节使用整个神经网络模型的实验中,不同模型的卷积核大小、权值位宽与稀疏率各不相同,于是IBTF 的简化效果也不同。为了更细致地验证IBTF 的简化效果,下面的实验将在单个卷积层中分析卷积核大小、权值位宽与稀疏率对IBTF 效果的影响。

卷积层的构造规则为固定输出特征图的大小为16,固定卷积核数量为M=4,卷积核大小分别取大卷积核N=1024 和小卷积核N=32 两种,权值数据位宽取值范围为1 ≤p≤8,符合主流神经网络模型量化后的权值位宽,当稀疏率设为λ(0 ≤λ <1)时,p比特权值w按式(6)随机生成,即以λ的概率取0,以1-λ的概率在2p -1 个非零取值中等概率随机选取。
对于权值稠密的卷积计算,假设所有权值参与计算,即λ=0,实验得到不同卷积核大小、不同权值位宽的卷积操作数统计如表2 所示。表中Eq_MAC_op为2.2 节中所述的等效MAC 操作数,表示IBTF 简化前的模型计算量;IBTF_op由式(5)得到最优切分后代入式(3)求得,表示IBTF 简化后的模型计算量;reduce rate=Eq_MAC_op/ IBTF_op,表示IBTF 将计算量减少的倍数。从该表中数据可得到如下2 个基本趋势:大卷积核情况下的IBTF 算法效果优于小卷积核;高位宽权值情况下的IBTF 算法效果优于低位宽权值。上述趋势的原因在于:当卷积核较大或权值位宽较高时,权值比特位重复更多且重复粒度更大,于是IBTF 消除的随之而来的无效计算更多且二进制权值张量的切分粒度更大,最终导致IBTF 算法的效果更显著。

表2 不同卷积核大小、不同权值位宽的卷积操作数统计
对于权值稀疏的卷积计算,固定卷积规模为输出特征图的大小为16;卷积核数量M=4;卷积核大小N=1024;权值位宽p=4。实验得到不同权值稀疏率的卷积操作数统计如表3 所示。从该表中数据可知,权值稀疏率越低,IBTF 效果越好。同理,该趋势原因为权值稀疏率低意味着非零比特位多,于是权值比特位重复更多且重复粒度更大。此外,实验结果表明,当权值稀疏率在80%~95%时(0.8≤λ≤0.95),即符合常见神经网络模型剪枝后的稀疏率取值,reduce rate取值为2.42~3.89。这一结果与3.2 节的常见神经网络模型中IBTF 平均使计算量进一步减少了3.32 倍相符。
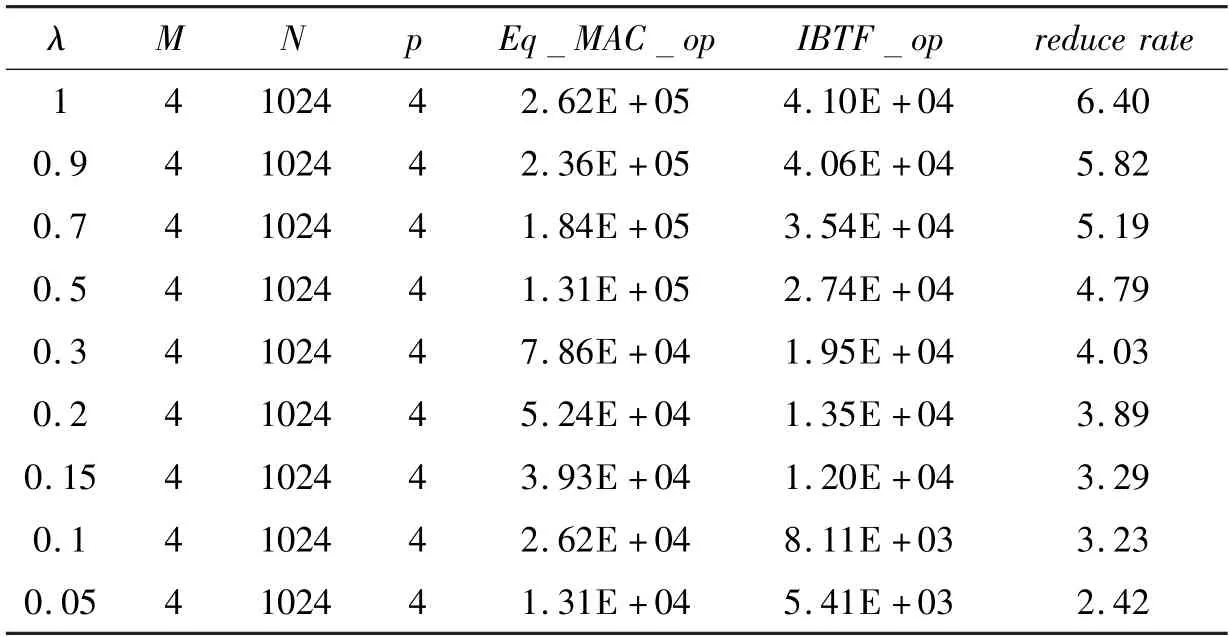
表3 不同权值稀疏率的卷积操作数统计
4 结论
本文从一种新的简化神经网络中卷积运算的角度出发,即消除权值比特位重复带来的计算重复,提出一种在比特级减少MAC 运算的乘加操作数的方法IBTF。它的主要优点有:(1)保持计算结果不变,不影响模型正确率;(2)不需要重训练;(3)与量化、稀疏等方法正交。效果上,在多个主流神经网络中,相较于量化与稀疏后的模型,IBTF 进一步使计算量减少了3.32 倍;并且IBTF 在不同规模、不同位宽、不同权值稀疏度的卷积运算中都发挥了显著的效果。未来将根据IBTF 算法设计硬件中的卷积运算单元,最终形成一个应用IBTF 的高能效神经网络加速器架构,从而将IBTF 实际应用于深度学习计算系统的加速中。

