Polya后验方法在有限总体抽样估计中的模拟研究

戴明锋，金勇进，孙婕

（中国人民大学a．统计学院；b．应用统计科学研究中心，北京 100872）

一、引 言

在抽样调查中，目标参数的估计通常有两种途径，一种是传统的基于频率学派的随机化抽样估计。Neyman提出了基于设计概率的抽样估计理论［1］7。这种理论认为观测样本的取值是固定的，没有误差的，唯一的随机性来源于抽取的样本。设计概率在频率学派的理论中起着非常重要的作用，很多估计量、比如总体均值、方差等的估计都是基于设计概率计算的，这种理论对目标量的统计分布不做专门的假设，因此在大样本的情况下，具有很好的性质。比如估计量的无偏性、稳健性、最小方差性等。π估计就是基于设计概率得出的计算总体估计量的一般公式。另一种目标量的估计基于模型的抽样估计，这种方法将总体取值视为随机过程，认为有限总体是从超总体模型中抽取的一个随机样本，是一个或多个随机过程的一次实现［2］。polya后验方法是基于模型估计的一种特殊形式，属于无信息贝叶斯方法。这种方法首先要对总体的分布进行一个假定，认为在样本抽取出来以后，后验分布即是在已知观测样本的条件下，没有观测样本的条件分布，抽样估计不应该依赖于设计概率。当总体只有少量或者几乎没有先验信息的情况下，polya后验方法能够得到很好地应用［3］。Rubin认为，polya后验方法类似于Bootstrap方法［4］。在国外，polya后验方法在分位数估计、小域估计中都得到了很好地应用［5－6］；而在国内，目前从事这方面的研究还比较少。本文对polya后验估计方法进行模拟研究，探讨了polya后验估计在有限总体抽样中的应用，并和运用比较成熟的Bootstrap方法进行比较，研究运用polya后验估计方法的一些估计效果。

二、polya后验抽样

（一）polya后验抽样过程

假设有两个盒子，第一个盒子中装有n个相同的球，每个球的观测值已知，记为y1，y2，…，yn，设这n个球为观测的一个样本。第二个盒子装有N－n个球（n＜＜N），观测值未知，现在分别从两个盒子中随机地各取一个球，假设从第一个盒子中取出的球的观测值为yi，令从第二个盒子中取出的球的值和从第一个盒子中取出的球的值相等，都为yi，然后将这两个球都放回第一个盒子中。再分别从两个盒子中随机地各取一个球，令从第二个盒子中取出的球的值和从第一个盒子中取出的球的值相同。将这个过程重复进行，直到这N－n个球都赋给了观测值。因此在给定观测样本的情况下，运用这种polya抽样就产生了未观测值的一个分布，这个分布称为polya后验分布。当这个过程完成后，就得到了总体的一个完全观测值。抽样过程如图1所示。

图1 polya后验抽样过程示意图

设m（y1，y2，…，yn）为边际密度函数，则给定一个样本统计量Z＝（s，y（s））和样本单元值y（s）＝（y1，y2，…yn）后，参数θ的后验密度为：

（二）polya后验估计过程

由于polya后验抽样估计属于无信息bayes估计，在进行点估计时，通常有以下步骤：1．确定参数的无信息先验分布；2．根据观测的样本信息，结合参数的无信息先验分布计算出未观测的样本的条件分布；3．定义一个损失函数；4．在损失函数下根据条件分布计算出相应的估计量。

设U＝｛1，2，…N｝表示容量为N 的有限总体，s＝｛1，2，…n｝为n的一个样本，样本单元数计为n（s），y（s）＝（y1，y2，…yn）为样本单元值，向量Y＝（y1，y2，…，yN）T是参数空间 Θ中的一个样本点，样本关于参数的所有信息包含在统计量Z＝（s，y（s））中。设B为参数空间Θ上的一个Borelσ代数，p为可测空间（Θ，B）上的一个测度。Bayes学派认为参数空间Θ上相应的先验分布属于先验分布族Π（θ）。

在具体计算条件分布时，首先需要确定先验分布和似然函数。无信息先验分布的分布函数可以选择π（θ）＝1或者选择Jeffreys先验分布，也可以选择其他的形式［7］。定义似然函数为：

记μ（y）为总体均值，在平方损失的情况下，总体均值的平均值为：

总体均值的方差估计为：

其中vs为样本方差，计算公式为：

三、polya后验方法特点的模拟研究

在复杂的统计问题中，有时候进行推导运算是很困难的，这时候可以借助统计模拟很好地解决问题。目前，统计模拟方法广泛用于很多统计问题的研究中［8］。本文利用R软件进行统计模拟，主要计算均值估计量、均值的置信区间、真值（总体均值）覆盖率。

在polya后验估计中，给定一个样本，产生一个完整的模拟总体，重复这个过程多次，进行点估计时，取每次估计值的平均值作为最终点估计值。在构造置信区间时，这里选择根据分位数构造置信区间。比如要构建均值的95%的置信区间，根据点估计得到一系列的均值，按照从小到大的顺序排序。取其下侧0．025分位数作为下侧置信区间，取其上侧0．975分位数作为上侧置信区间。

设有两个总体，记为pop1和pop2，各包含10 000个单元。pop1服从均值为100方差为20的正态分布；pop2服从位置参数为20尺度参数为5的伽马分布。在每个总体中，分别抽取样本量为1 000、2 000、3 000、4 000的四个样本，每种情况模拟500次。计算均值的估计值、置信区间以及真值（总体均值）覆盖率。模拟结果如表1。

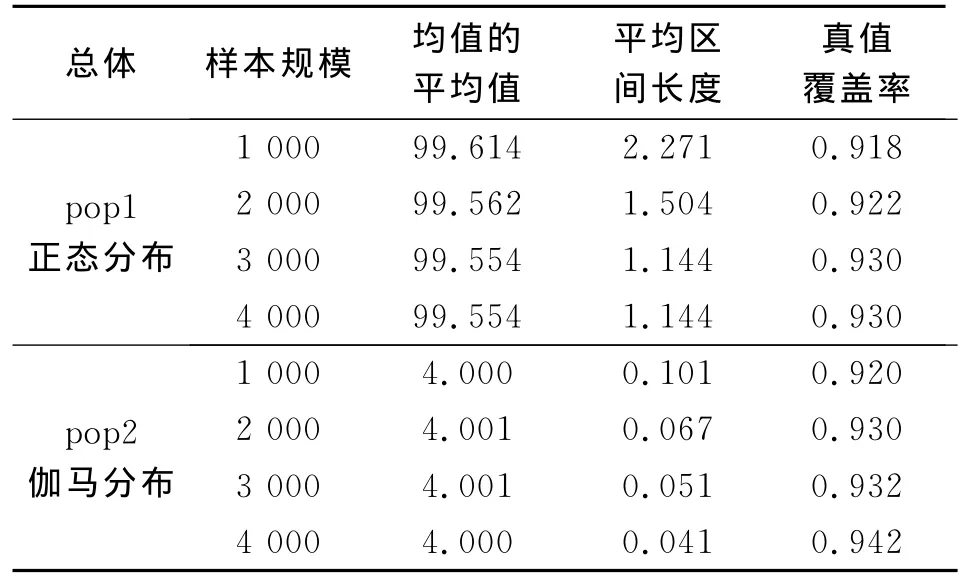
表1 polya后验估计的模拟结果

在设定好随机种子后，pop1中，本文中利用总体10 000个样本单元直接计算出的总体均值是99．984；pop2中，利用总体10 000个样本单元直接计算出的总体均值是3．984。对比表1中显示的估计结果，可以看出采用polya后验估计可以精确地估计出总体的均值。当样本量增加时，均值的平均置信区间会变短，但是真值覆盖率会增加。pop1中，可以看到当样本容量由3 000增加到4 000后，平均区间长度和真值覆盖率并没有发生变化，说明当样本量增加到一定程度后，采用这种方法估计的精确度就会稳定在一定水平上。pop2中，当样本容量由3 000增加到4 000后，平均区间长度和真值覆盖率虽然发生了一定的变化，但是变化幅度已经非常小了。

四、polya后验估计与Bootstrap方法估计的模拟比较

（一）Bootstrap方法的基本原理

Bootstrap方法是一类非参数蒙特卡洛方法，它通过再抽样对总体分布进行估计，再抽样方法将观测到的样本视为一个有限总体，从中进行随机再抽样来估计总体的特征以及对总体参数作出统计推断［9］。

假设y＝（y1，y2…，yn）为从一个总体分布F（y）中观测的样本，Y＊为从y中随机选择的一个样本，则P（Y＊＝yi）＝，i＝1，2，…，n，从y中有放回的再抽样得到随机样本Y1＊，Y2＊，…，Yn＊，则随机变量Y1＊，Y2＊，…，Yn＊为独立同分布的随机变量，服从｛y1，y2…，yn｝上的均匀分布。

由于经验分布函数Fn（y）是F（y）的估计，并且其本身是｛y1，y2…，yn｝上的均匀分布随机变量Y＊的分布函数。因此Bootstrap重复下的经验分布函数Fn＊是Fn的逼近。从y中再抽样，等价于从Fn中产生随机样本。

采用Bootstrap方法构造置信区间可以采用标准Bootstrap、百分位数Bootstrap、t百分位数Bootstrap和修正偏差后的百分位Bootstrap四种方法来估计。本文采用百分位数Bootstrap方法。

百分位数Bootstrap方法利用Bootstrap经验分布的和1－分位点分别是在1－α置信水平下统计量T的置信区间的上、下限。具体如下：假设取B＝1 000时，可以得到1 000个Bootstrap随机样本，将每个样本的均值按由小到大的顺序依次排列，可以得到顺序统计量（i），（i＝1，2，…B），则和 1－分位点分别是在1－α置信水平下统计量T的置信区间的上下限。

根据伯努利大数定理，，当抽样次数充分大时，这些区间中包含θ的真值的频率接近于置信度（即概率）1－α，即在这些区间中包含θ的真值的区间大约有100（1－α）%个，不包含θ的真值的区间大约有100α%个。

（二）polya后验估计与自Bootstrap方法估计的模拟比较

设有四个总体，记为pop1、pop2、pop3和pop4，各包含1 000个单元。pop1服从区间（－1，1）上的均匀分布，pop2服从均值为10方差为1的的正态分布，pop3服从位置参数为5尺度参数为1的伽马分布，pop4服从参数为4的指数分布。在每个总体中，分别抽取样本量为100、200的两个样本，每种情况模拟500次。计算在Bootstrap方法和polya后验方法下均值的估计值、置信区间以及真值（总体均值）覆盖率。模拟结果如表2。

表2显示：总体来看，在pop1、pop2、pop3、pop4四个分布不同的总体中，采用Bootstrap方法和polya后验估计估计时，在估计总体均值时，二者没有什么大的区别，样本量发生变化后，采用两种方法估计的总体均值差异也差不多。在构造的平均置信区间方面，采用polya估计方法构造的置信区间区间长度相对较短，而采用Bootstrap方法构造的置信区间区间长度相对较长一些。在真值覆盖率方面，采用Bootstra方法估计时，真值覆盖率要高一些，但是采用polya后验方法也能以较高的概率覆盖真值。

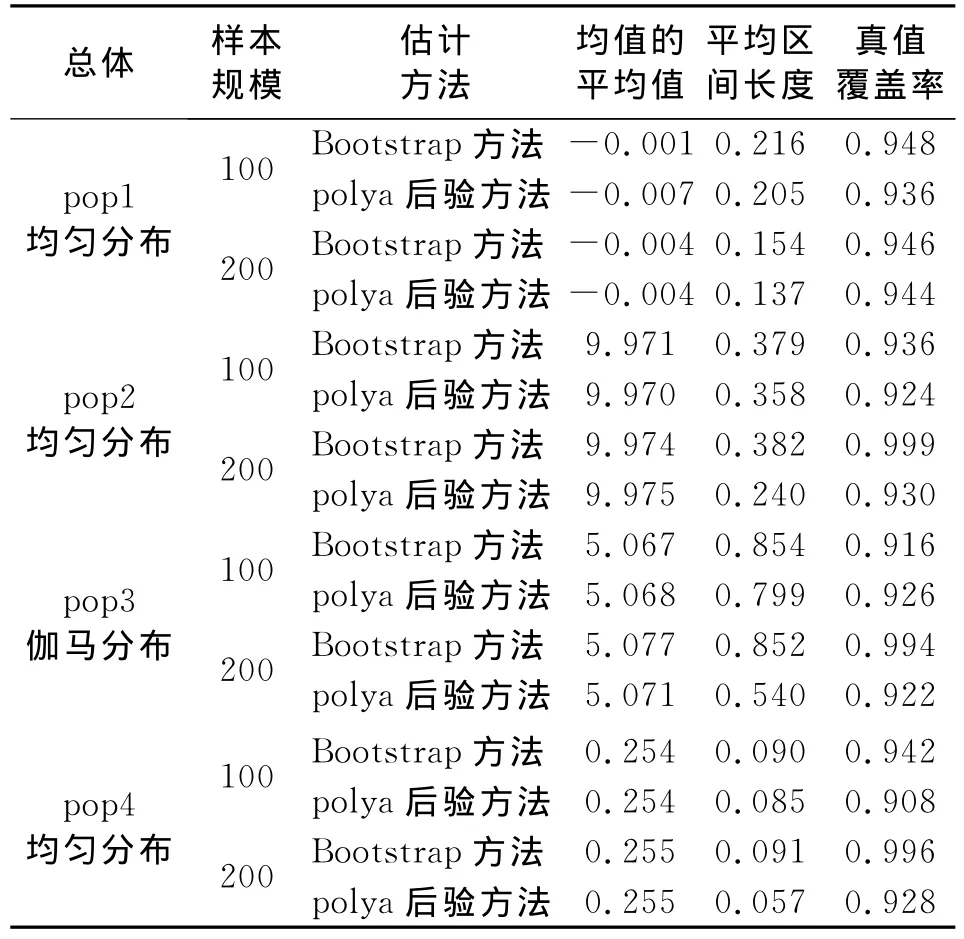
表2 polya后验估计与Bootstrap估计的结果比较表

五、小 结

本文研究了polya后验方法在有限总体抽样中的应用，通过模拟研究，发现polya后验估计可以精确地估计出总体的均值，据此构造的置信区间相比较根据Bootstrap方法构造的置信区间长度较短一些，置信区间能够以较高的概率覆盖真值。对于polya后验估计在估计方差时效果如何，polya后验估计的使用范围，以及polya后验方法在实际问题中的应用等一些问题，还需要进一步的研究。

［1］ Cochran W G．抽样技术［M］．张尧廷，吴辉，译．北京：中国统计出版社，1985．

［2］ 金勇进，贺本岚．复杂抽样推断方法体系的比较研究［J］．统计与信息论坛，2011（10）．

［3］ Glen Meeden．A Noninformative Bsyesian Approach to Domain Estimation［J］．Journal of Statistical Planning and Inference，2005（12）．

［4］ Rubin D．The Bayesian Bootstrap［J］．Annals of statistics，1981（9）．

［5］ David Nelson，Meeden Glen．Noninformative Nonparametric Quantile Estimation for Simple Random Samples［J］．Journal of Journal of Statistical Planning and Inference，2006（9）．

［6］ Xiaoyin Wang，Chong Z He，Dongchu Sun．Bayesian Population Estimation for Small Sample Capture-Recapture Data Using Noninformative Priors［J］．Journal of Statistical Planning and Inference，2007（4）．

［7］ 茆诗松，王静龙，濮晓龙．高等数理统计 ［M］．北京：高等教育出版社，1998．

［8］ 杨贵军，刘艳林，王清．捕获在捕获抽样估计量的模拟研究 ［J］．统计与信息论坛，2011（3）．

［9］ 谢益辉，朱钰．Bootstrap方法的历史发展和前沿研究［J］．统计与信息论坛，2008（2）．