p-范分布中参数的置信区间

李双双，胡宏昌

(湖北师范大学 数学与统计学院，湖北 黄石 435002)

0 引言

在处理数据时，当观测误差为单峰、对称分布时，可以假设其服从p-范分布。已有许多学者对p-范分布进行了深入研究，如：文献[1]定义了χp分布、tp分布、Fp分布，并给出了它们的密度函数，为p-范分布的进一步研究提供了便利；文献[2]得到了在不同情况下p-范分布各个参数的计算公式；文献[3]研究了p-范分布的假设检验，对μ,p进行了U检验，对单总体的σ进行了χp检验，对双总体的σ进行了Fp检验，文中的统计量对本文中的枢轴量的确定极为重要。文献[4]表明p范分布可以近似地表示为拉普拉斯分布与正态分布或可表示为正态分布与均匀分布的线性组合，在解决相关问题时，用近似分布来代替p范分布会让其更简单。文献[5～10]也都对p范分布进行了深度研究。

尽管学者们对于p-范分布的研究成果十分丰富，但关于p-范分布各参数的置信区间的研究还未提到，因此本文对于p-范分布的各单个参数的置信区间进行了研究。基于已有的相关结论，确定合适的枢轴量及其分布，用枢轴量法确定p-范分布中各参数在不同情况下的置信区间或近似置信区间。

1 p-范分布及其抽样分布

为了求p-范分布各参数的置信区间，我们简要介绍p-范分布及其抽样分布，详见文献[1]。

定义1 令Γ(x)为伽玛函数，λ=[Γ(3/p)/Γ(1/p)]1/2，则期望为μ，方差为σ2的一元p-范分布的密度函数为

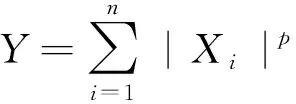
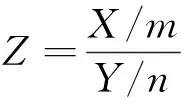
其中B(x,y)为贝塔函数。

2 单总体的参数置信区间

设X1,X2,…,Xn是从p-范分布总体X抽出的容量为n的子样，观测值为x1,x2,…,xn.

2.1 μ的置信区间

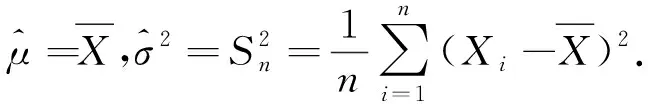
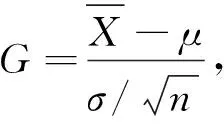
2) 当σ未知时，σ用矩估计代替，得μ的1-α近似置信区间为

2.2 σp的置信区间

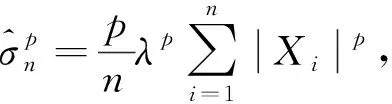
2) 当μ未知时，用矩估计代替，得σp的1-α近似置信区间为

2.3 h(p)的置信区间

当μ,σ已知，不妨设为μ=0，σ=1，由文献[3]知

h(p)=Γ(1/p)Γ(5/p)/Γ2(3/p)

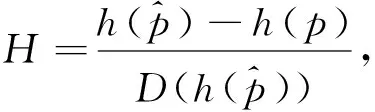
3 双总体的参数置信区间

设X1,X2,…,Xn1是从总体X(三个参数为μ1,σ1,p1)抽出的容量为n1的子样，观测值为x1,x2,…,xn1；Y1,Y2,…,Yn2是从总体Y(三个参数为μ2,σ2,p2)抽出的容量为n2的子样，观测值为y1,y2,…,yn2.

3.1 μ1-μ2的置信区间

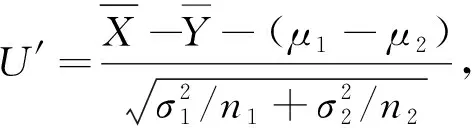
2) 当σ1,σ2未知时，用矩估计代替，得μ1-μ2的1-α近似置信区间为

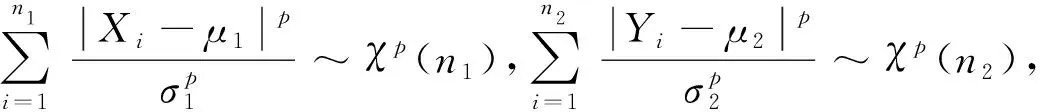
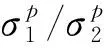
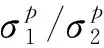
3.3 h(p1)-h(p2)的置信区间

同2.3节一样，不妨假设μ1=μ2=0,σ1=σ2=1，由文献[3]知

h(p1)=Γ(1/p1)Γ(5/p1)/Γ2(3/p1)

h(p2)=Γ(1/p2)Γ(5/p2)/Γ2(3/p2)

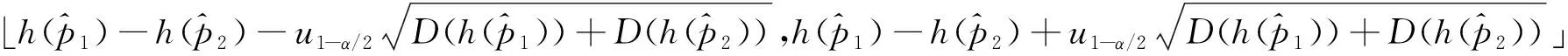
4 模拟算例

例1 单总体的参数μ的置信区间

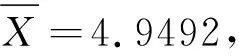
[4.7532,5.1452]，包含真值μ=5.

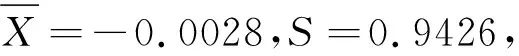
例2 单总体的σp的置信区间

在(1)式中，令p=2.4,μ=0,σ=1，随机生成100个随机数。

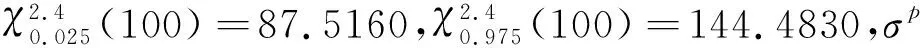
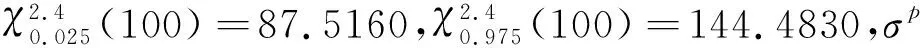
例3 单总体p的置信区间

在(1)式中，令p=1,μ=0,σ=1，随机生成100个随机数。

设总体的μ=0，σ=1，α=0.05,u1-α/2=1.96，通过计算得h(p)的置信水平为0.95的近似置信区间为[4.7477,22.5826]，进一步计算得p的置信水平为0.95的近似置信区间[0.52,1.20]，包含真值p=1.

例4 双总体的μ1-μ2的置信区间

在(1)式中，令p=1.6,μ=0,σ=1，两次分别随机生成120个随机数，分别记为X1,X2,…,X120,Y1,Y2,…,Y120.

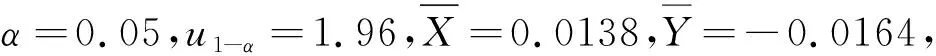
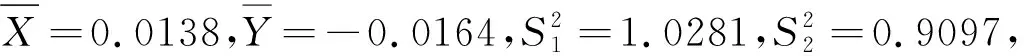
在式(1)中令p=1.4,μ=0,σ=1，两次分别生成120个随机数，分别记为X1,X2,…,X120,Y1,Y2,…,Y120.

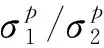
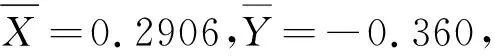
例6 双总体的p1-p2的置信区间

在式(1)中令p=1.4,μ=0,σ=1，两次分别生成120个随机数，分别记为X1,X2,…,X120,Y1,Y2,…,Y120.已知μ1=μ2=0,σ1=σ2=1，计算得

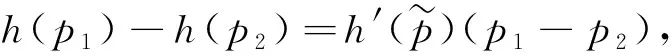
[-1.4686,0.5388]，包含真值p1-p2=0.

5 结论

上面研究了p-范分布的三个参数在不同情况下的(近似)置信区间，并通过模拟算例证明了上述置信区间的结论是可靠的。虽然在一定程度上丰富了p-范分布置信区间的内容，但对于p-范分布置信区间的研究不止于此，本文所得出的置信区间还不够精确，为了得到进一步的精确结果还需要更进一步的研究。