基于最佳一次逼近多项式的求平方根迭代法
何斯日古楞
(呼和浩特民族学院 数学与大数据学院,内蒙古 呼和浩特 010051)
平方根计算虽是一种古老的问题[1],但被广泛用于现代数学和工程计算。算数平方根计算主要用于信号处理[2]、微机保护装置[3]和微处理器计算[4]等。嵌入式微处理器无专门的开方指令,需借助牛顿迭代法和逐位循环[5]等算法实现开方。文献[2~5]研究开方算法的硬件实现,然而相关理论分析甚少。文献[6]介绍了基于二项展开式的逐位近似算法及其发展历史。

1 迭代公式的推导以及收敛分析
定理1[7,8]设f(x)是区间[α,β]上的连续函数,令Hn表示所有次数不超过n的多项式以及零多项式构成的集合。P(x)∈Hn是f(x)的最佳逼近多项式的充要条件是P(x)在[α,β]上至少有n+2个轮流为“正”“负” 的偏差点,即有n+2个点α≤x1 设a>0,xk-1,xk为二次方程f(x)=x2-a=0的两个已知近似根,且不妨假设xk-1 因此,函数g(x)=P(x)-f(x)满足g(y1)=g(y3).又由于f″(x)在[xk-1,xk]上不变号,故f′(x)单调。于是用罗尔中值定理知,g′(x)=a1-f′(x)在(xk-1,xk)内只有一个零点,记为y2,即 g′(y2)=a1-f′(y2)=0.另外两个偏差点必在区间端点,即y1=xk-1,y3=xk,且满足 P(y1)-f(y1)=P(y3)-f(y3)=-[P(y2)-f(y2)] 于是,解得 进而,求解P(x)=0可得迭代公式(1) (1) 证明 由迭代公式(1)可得 (3) 又从迭代公式(1)和(3)式,有 (4) 据此反复递推,得 (5) 又由假设x0=x1,知e0=e1.因此,对(6)式反复递推,有 即 证明 对已知迭代值xk-1,xk,二次方程f(x)=x2-a=0的弦截格式为 相应的误差方程为 此外,对给定的迭代值xk-1,xk,误差方程 (2) 可写成 进一步,有 注意到,利用定理3的结论,可得 进而,有 表的数值计算结果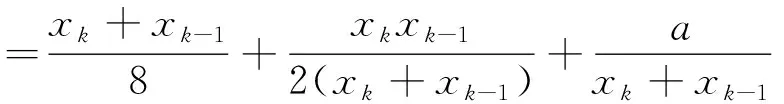

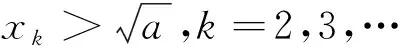

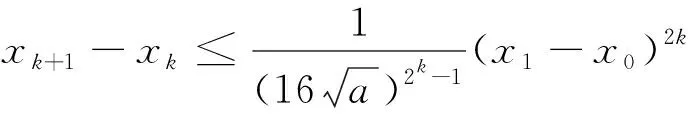
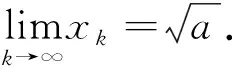
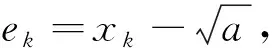

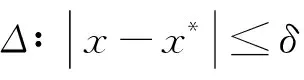
2 数值例子与结论