微积分思想和方法在大学物理教学中的应用和研究

黄 熙，饶 识，谭艳蓉，郭健勇，陈飞明，管 薇，胡中华，许明耀

(1. 武汉纺织大学 数理科学学院，湖北 武汉 430200；2. 湖北工业大学 理学院，湖北 武汉 430068)

0 引言

《大学物理》是大专院校理、工科学生必修的一门全校公共基础课程，通过该课程的学习，可以使学生掌握基本的物理概念、物理思想、物理方法以及提高分析问题、解决问题的能力。学习《大学物理》[1～4]要借助于《高等数学》中的矢量分析、导数和微积分的运用等内容[5,6]，所以在教学计划中该课程一般是安排在大一下学期和大二上学期，学生先要修完《高等数学》。然而，正是由于学生掌握高等数学的基础不扎实，没有真正理解导数、微积分的意义，导致学生在学习《大学物理》信心不足甚至有畏难情绪。当然，《大学物理》挂科率高除了上述谈到的客观原因外与学生自身的主观原因也是密切相关，其详细原因以及应对的措施可以参考文献[7]。本文重点探讨微积分在大学物理中的应用，包括极限思想、微元、积分方向、标量和矢量求导、标量和矢量积分、微积分方法、导数和积分的几何意义等方面。

1 微积分在大学物理中的应用

《微积分》是十七世纪由英国科学家牛顿和德国数学家莱布尼茨分别独自创立的，牛顿是从运动学角度研究微积分，而莱布尼茨侧重于几何学来考虑的。利用微积分来处理运动学和几何学的问题，归纳起来有以下四类：第一类问题是研究运动学时求瞬时物理量，比如瞬时速度、瞬时加速度等；第二类问题是求曲线的切线；第三类问题是求函数的极值，比如极大值和极小值；第四类问题是求曲线长、曲线围成的面积和体积、物体的重心等。下面，我们具体讨论微积分在大学物理中的应用。

1.1 极限思想

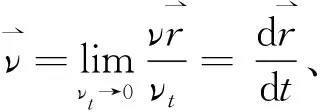
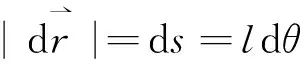
(a) (b)

1.2 微元

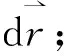
(a) (b)

1.3 积分方向

1.4 标量和矢量求导、标量和矢量积分

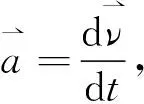
例题1：如图3所示，正电荷q均匀分布在半径为R的圆环上。计算通过环心点O并垂直圆环平面的轴线上任一点P处的电场强度。

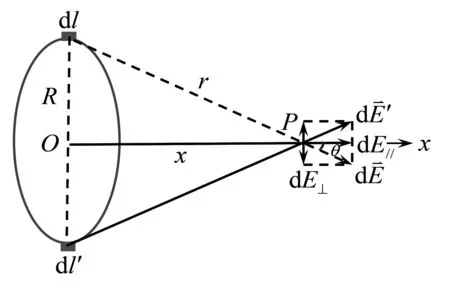
图3 例题1

根据几何关系，可得

1.5 常见的微积分方法

在《大学物理》所用到常见的微积分方法简单地总结一下有：以直代曲法、分离变量法和积分常量提出法等[8]。以直代曲法的核心思想就是极限思想，在求变力做功、在非均匀电(磁)场穿过形状任意曲面的电(磁)通量、形状任意的载流导线在非均匀磁场所受的安培力等都有应用。举一个大家比较容易理解的例子——求曲边梯形面积：把曲边梯形分割成许多要有多小就有多小的矩形，对所有矩形的面积求和即曲边梯形的面积。

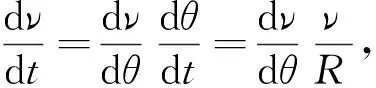
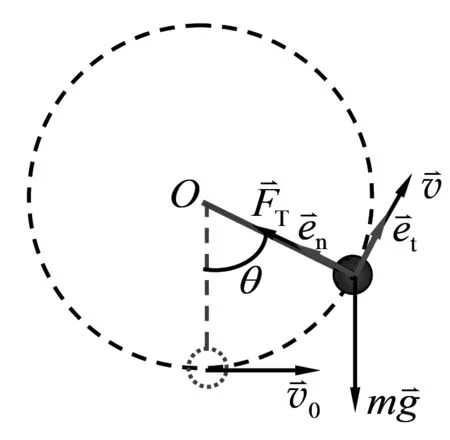
图4 例题2

解：由小球受力分析，根据牛顿第二定律，列出分量式

FT-mgcosθ=man

(1)

-mgsinθ=mat

(2)

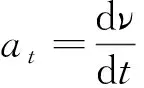
FT-mgcosθ=mν2/l

(3)

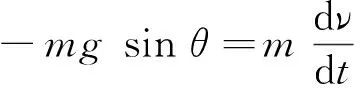
(4)

对(4)式直接分离变量求解，计算不出速率ν，必须将积分变量进行转换，即

分离变量，方程两边同时取定积分，有

求得

(5)

图5 重力做功示意图

1.6 导数和积分的几何意义

2 结束语

以上我们总结了导数、微积分在大学物理中的应用，包括极限思想、微元、积分方向、标量和矢量的求导和积分、微积分方法和导数、积分的几何意义。通过探讨导数、微积分在大学物理中的应用，可以使学生、教师对导数、微积分的物理和几何意义有更深入地理解和掌握。教学质量是教学的生命线，只有掌握好导数、微积分等基本应用，才能进一步提高大学物理教学质量[9]。当然，导数和微积分作为《高等数学》的基本知识点在其他学科也有很多方面的应用，所以把握好导数和微积分对于学习其他学科可以起到事半功倍的效果。