一种高效的椭圆曲线密码标量乘算法及其实现
时丽平,王子健
(河南质量工程职业学院,河南 平顶山 467000)
0 引 言
椭圆曲线密码(Elliptic Curve Cryptography, ECC)是于1985年由Koblitz和Miller分别提出的,其安全性是建立在求解椭圆曲线离散对数问题ECDLP困难性的基础之上[1-2]。与传统公钥密码相比,椭圆曲线密码算法具有密钥长度短、安全性能高、计算量小、处理速度快、存储空间占用少、带宽要求低等优点,所以椭圆曲线密码算法当前广泛应用于各种存储受限的环境中。椭圆曲线密码中最基本的运算是标量乘法运算,其也是提高椭圆曲线密码效率的关键运算。为有效提高椭圆曲线密码运算效率,国内外研究人员也提出了许多提高标量乘运算效率的方案[3-4]。其中,经典的椭圆曲线密码标量乘算法有二进制标量乘算法、NAF标量乘快速算法和基于窗口的NAF标量乘快速算法等。椭圆曲线密码标量乘法运算是指已知域内一整数k与椭圆曲线上一点P,求解椭圆曲线上另一点Q=kP的运算。在具体运算执行过程中,标量乘法运算是按照一定的编码方法扫描标量k,然后通过不断调用点加运算与倍点运算来实现的,而点加运算与倍点运算则是通过不断调用有限域加减法与乘法来完成的。由于大多数用于提高标量乘法运算的改进方法都是侧重考虑性能,甚至是通过牺牲存储空间来换取高运算效率,使得各种提出的改进算法的应用受到了限制[5-6]。为有效减少标量乘法运算的存储空间,给出了一种基于彼此相反型编码的标量乘算法(Scalar Multiplication algorithm based on Mutual Opposite Form coding, SMMOF)。该算法采用彼此相反型编码方式对标量进行重新编码来实现标量乘法运算,而且在满足约束条件的前提下通过尽可能充分利用SRAM空间可以有效降低IP的面积。与从右向左NAF编码的标量乘算法相比,所给SMMOF算法在保持原有性能的情况下,其IP面积缩减了10%左右。
1 传统标量乘算法分析
经典的椭圆曲线密码标量乘算法有平方-乘法标量乘算法、NAF编码标量乘算法与基于窗口的NAF标量乘算法等。下面从存储空间和性能两方面对这三种算法进行分析。
1.1 平方-乘法标量乘算法
平方-乘法是椭圆曲线密码中最基本的标量乘算法,主要是将标量k采用二进制编码的形式进行编码。其编码形式如下式(1)所示:
(1)
其中,ki为平方-乘法编码系数,且有ki∈{0,1},n为标量的二进制编码长度。按照从左向右的扫描方向,则有基于平方-乘法的标量乘算法如算法1所示。
算法1 从左向右基于平方-乘法的标量乘算法
输入:标量k,椭圆曲线上一点P;
输出:Q=kP。
1. 令Q=O;
2. 计算标量k的二进制编码k=(kn-1,kn-2,…,ki,…,k1,k0)2;
3. 对于i从n-1到0,则重复执行:
3.1Q=2Q;
3.2 如果ki=1,则有Q=Q+P;
4. 返回Q。
在执行效率方面,标量k的二进制表示中比特位为1的期望值是n/2,则算法1的运算量为nD+(n/2)A。由于算法1在混合坐标系下的效率更高,所以采用混合坐标计算算法1的运算量。令M表示模乘运算,S表示模平方运算,且有S≈0.8M。则可知算法1的运算量为n·(4M+6S)+(n/2)·(9M+3S)=14.5nM。在存储空间方面,算法1只需存储坐标即可。
1.2 NAF算法
二元非相邻形式(Non-adjacent Form, NAF)[7]编码是指在标量k的二进制序列中的每个位包含0、1和-1三种形式,且不会有相邻的非零元素出现。其具体编码形式如下式(2)所示:
(1)
其中,ki为NAF编码系数,且有ki∈{-1,0,1}以及km-1≠0,m为NAF编码长度。按照从左向右的扫描方向,则有基于NAF编码的标量乘算法如算法2所示。
算法2 从左向右基于NAF的标量乘算法
输入:标量k,椭圆曲线上一点P;
输出:Q=kP。
1. 令Q=P;
2. 计算h=3k=(hm-1,hm-2,…,h1,h0),其中hm-1=1。将标量k也写成二进制编码形式k=(km-1,…,ki,…,k1,k0);
3. 对于i从m-2到0,则重复执行:
3.1Q=2Q;
3.2 如果hi=1且ki=0,则有Q=Q+P;
3.3 如果hi=0且ki=1,则有Q=Q-P;
4. 返回Q。
在执行效率方面,标量k的NAF编码长度最多比二进制编码长度多1位,但NAF编码中平均非零个数约为1/3。则可知算法2的运算量为m·(4M+6S)+(m/3)·(9M+3S)=12.6mM。在存储空间方面,算法2比算法1需要多存储一个参数h=3k。
1.3 NAFw算法
基于窗口的NAF编码(NAFw)[8]标量乘算法是NAF编码标量乘算法的改进算法,主要是利用预计算来提供标量乘法运算的速度。令窗口宽度w是正整数,则有NAFw编码表示形式如下式(3)所示:
(3)
其中,|ki|<2w-1为NAFw编码系数且为奇数,任何连续的w个位中最多有1位非零,l为NAFw编码长度。按照从左向右的扫描方向,则有基于NAFw编码的标量乘算法如算法3所示。
算法3 从左到右基于NAFw编码的标量乘算法
输入:标量k,椭圆曲线上一点P;
输出:Q=kP。
1. 令Q=O;
2. 计算标量k的NAFw编码k=(km-1,…,ki,…,k1,k0)NAFw;
3. 预计算Pi=iP;//其中,i∈{1,3,5,…,2w-1-1}
4. 对于i从l-1到0,则重复执行:
4.1Q=2Q;
4.2 如果ki>0,则有Q=Q+Pki;
4.3 如果ki<0,则有Q=Q-P-ki;
4. 返回Q。
在执行效率方面,标量k的NAFw编码中平均非零个数约为1/(w+1)。则可知算法2的运算量为(l+1)·(4M+6S)+((2w-2-1)+l/(w+1))·(9M+3S)=20.2((2w-2+l)+l/(w+1))M。在存储空间方面,算法3除了需多存储一个参数NAFw(k),还需要多存储2w-2个预计算值。基于NAFw编码的标量乘算法是以额外的存储空间来换取执行效率的提高,不适用于存储空间受限的密码设备中。
2 SMMOF算法设计
彼此相反型编码(Mutual Opposite Form, MOF)[9]的定义包括三个方面特点:(1) MOF编码的最高非零比特为1;(2) MOF编码除最低非零比特位外,中间比特位的形式为(x0)后接符号与x符号相反的非零比特,或者为(0x)后接与x符号相同的非零比特,不考虑(x0)或(0x)后出现0的情况,其中|x|=1;(3) MOF编码的最低非零比特可能为最后一个比特。则有基于MOF编码的标量乘算法如算法4所示。
算法4 基于MOF编码的标量乘算法
输入:标量k,椭圆曲线上一点P;
输出:Q=kP。
1. 计算标量k的MOF编码MOF(k)=(kt-1,kt,…,ki,…,k1,k0);
2. 从MOF编码最高位扫描标量k,直到找到非零比特记为i;
3. 如果k[i-1]=0,则有Q=P,i=i-2;
如果k[i-1]=1,则有Q=2P,i=i-2;
4. 对于i≥1时,则执行:
4.1 如果k[i]=k[i-1],则有Q=2Q,i=i-1;
4.2 如果k[i]≠k[i-1]且(k[i],k[i-2])=(1,1),则有Q=2Q,Q=2Q,Q=Q-P,i=i-2;
4.3 如果k[i]≠k[i-1]且(k[i],k[i-2])=(1,0),则有Q=2Q,Q=Q-P,Q=2Q,i=i-2;
4.4 如果k[i]≠k[i-1]且(k[i],k[i-2])=(0,1),则有Q=2Q,Q=Q+P,Q=2Q,i=i-2;
4.5 如果k[i]≠k[i-1]且(k[i],k[i-2])=(0,0),则有Q=2Q,Q=2Q,Q=Q+P,i=i-2;
5. 如果i=0且k[i]=0,则有Q=2Q;
如果i=0且k[i]=1,则有Q=2Q,Q=Q-P;
6. 返回Q。
标量k的MOF编码长度最多比二进制编码长度多1位,且其平均非零个数约为1/3,可见其继承了NAF编码的优良性质。由于基于MOF编码的标量乘算法可以从左向右动态生成,所以可以省去存储标量编码的存储空间。在执行效率方面,算法4与算法2相当。在存储空间方面,算法4不需要额外的存储空间,与算法1基本相当。
3 SMMOF算法实现
若要达到最大降低存储开销的目的,则要使标量乘算法与操作数放置策略很好配合。算法4所给的SMMOF标量乘算法可以很好地减小存储空间,可以较好地用于存储空间受限的移动设备中,具体实现框架如图1所示。
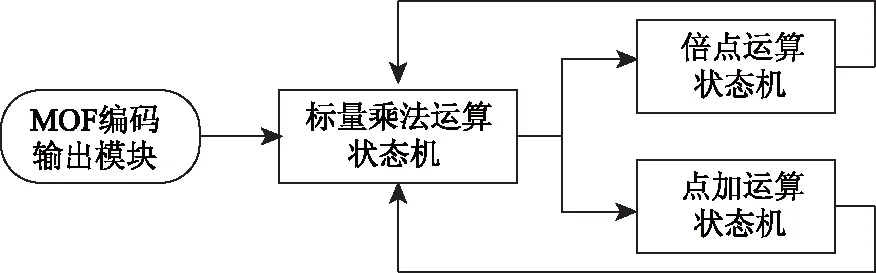
图1 所给SMMOF标量乘算法实现框架图
其中,MOF编码输出模块主要是从左向右输出标量k的每一位比特,标量乘法运算状态机根据输入的比特产生相应的控制信号来调用倍点运算状态机与点加运算状态机,最后倍点运算状态机与点加运算状态机将计算结果反馈到标量乘法运算状态机。由于椭圆曲线密码标量乘法运算中的操作数包括坐标点、临时变量曲线参数等很多且均为很大的数,所以为减少面积开销,采用SRAM存放这些操作数。然而,由于SRAM在一个周期内仅能读取或写入一个字,所以为了不影响底层域模块的执行效率,应把需要同时存取的操作数存放在不同的SRAM中。标量乘算法底层域模块对于操作数的放置主要包括如下两个方面约束:(1) 模加减运算A+B=DmodN,其中A,B,D,N存放在不同的SRAM中,但两个操作数相同或是某一操作数为N的除外;(2) 模乘运算A×B=TmodN,其中模乘器为二级流水线实现,要求其同时能对T进行读写,A,B,T存放在不同的SRAM中,但两个操作数相同的除外。因此,采用四块56×32的单口SRAM与一块24×32的双口SRAM。其中,SRAM的操作数放置策略如表1所示。

表1 SRAM的操作数放置策略
在操作数放置策略中,将每一块单口SRAM分成3个部分,每一部分用来存放一个大数,而双口SRAM作为整体存放一个大数。其中,a与N为曲线参数,k为标量,Px与Py为椭圆曲线某点坐标,这些参数是在计算前必须向ECC IP输入的参数。Const为点加运算中需用到的一个重要参数,其取值对于固定曲线而言是不变的,所以可将其作为常量预先计算出来;R2为点加运算中用到的一个重要参数,但由于其仅用于预计算,因而可在后面运算中提前释放存储空间用于存放其他临时变量。Sx、Sy与Sz主要是用于存放最后标量乘法运算的结果。tmp0专门用于存放模乘运算的临时结果T,其他tmp主要都是用于存放倍点运算与点加运算中的临时变量。
4 算法性能分析
在素数域ECCIP中采用所给SMMOF标量乘算法以及从右向左的NAF编码标量乘算法[10],且操作数的放置符合约束条件,然后比较其IP的性能和占用面积。下面表2给出了IP运行频率在100 M赫兹时,所给SMMOF标量乘算法与从右向左的NAF编码标量乘算法在不同NIST椭圆曲线下的标量乘法运算的性能。

表2 100M赫兹时NAF编码标量乘与所给SMMOF标量乘的执行效率比较(次/s)
由表2可以看出,采用所给SMMOF标量乘算法的IP基本能够保持原来的性能,甚至是优于基于从右向左的NAF编码标量乘算法的IP性能。基于SMIC 0.18 μm工艺,100 M赫兹频率,采用Synopsys dc对所给SMMOF标量乘算法及基于从右向左的NAF编码标量乘算法的IP进行综合。基于从右向左的NAF编码标量乘算法IP的面积为95k门,其中SRAM需要52k门左右;所给SMMOF标量乘算法IP的面积为86k门,其中SRAM需要45k门左右。由此可见,采用所给SMMOF标量乘算法IP的面积要比基于从右向左的NAF编码标量乘算法IP的面积减小了约10%。因此,所给SMMOF标量乘算法可以在不牺牲性能的前提下有效缩减IP面积,可很好地应用在资源受限的密码设备中。
5 结 语
椭圆曲线密码算法是应用最为广泛的公钥密码算法之一,其中标量乘法运算的性能是影响其应用的关键运算。为有效降低标量乘法运算的存储空间,给出了一种基于MOF编码的标量乘算法。所给SMMOF标量乘算法主要是利用MOF编码对标量进行重新编码,可以动态地实现从左向右的标量乘算法,与基于NAF编码标量乘算法相比具有大致相当的执行效率,与基于平方-乘法的标量乘算法相比具有基本类似的存储空间。所给SMMOF算法可以在不牺牲性能的前提下有效降低存储空间。操作数存放策略是在满足约束条件的前提下尽可能充分利用全部SRAM空间,通过比较采用从右向左的NAF标量乘算法IP与采用所给SMMOF标量乘算法IP的性能和面积,可以看出采用所给SMMOF标量乘算法IP的面积比采用从右向左的NAF标量乘算法IP的面积减少了10%左右,同时还能够保持与从右向左的NAF标量乘算法相当的性能。因此,所给SMMOF算法可很好地应用在资源受限的密码设备中,具有较好理论研究价值和实际推广应用价值。

