一种基于前后向Toeplitz矩阵重构的相干信号DOA估计算法

唐晓杰，赵 迪，何明浩，袁 浩 ，薛永辉

(1.空军预警学院，湖北 武汉 430019; 2.中国人民解放军31435部队，辽宁 沈阳 110000; 3.中船重工武汉凌久电子有限责任公司，湖北 武汉 430019)

0 引 言

到达角(direction-of-arrival, DOA)估计是信号处理领域的重点研究问题之一，在雷达、通信、电子对抗领域均有着广泛的运用[1-4]。信号在传播过程中，容易受到地形、气候和环境的影响，产生折射、反射，形成相干信号，在处理相干信号时，传统的DOA估计算法性能下降，甚至失效[5]，因此，相干信号DOA估计算法一直以来都是研究热点。

前向空间平滑(Forward Spatial Smooth, FOSS)算法[6]是最早进行相干信号DOA估计的方法，其孔径损失严重，当阵元数为M时，能估计的到达角至多只有M/2个。为了增大孔径，获得更高的测向自由度，Pillai等人提出了前后向空间平滑(Forward and Backward Spatial Smooth, FBSS)算法[7]，FBSS利用了后向子阵列，增加了平滑次数，能够估计至多2M/3个到达角。FOSS和FBSS算法仅恢复了数据协方差矩阵的秩，并没有完全消除信号的相干性。文献[8]提出了一种ESPRIT-like算法，将数据协方差矩阵的任意一行构造成Toeplitz矩阵，能够完全消除信号的相干性，进而可以利用ESPRIT算法进行DOA估计，但该算法数据丢失严重，估计精度不高。文献[9]提出了一种基于前后向矢量重构的CVM算法，利用数据协方差矩阵中的两行数据进行矩阵构造，但其数据利用率仍较低。文献[10]提出了一种序贯分组的相干信号分组估计方法，提高了精度和最大可分辨信号数，但是算法复杂度较高，且需要每组相干信号数先验信息。文献[11]提出了一种主奇异矢量模态分析法(principal-singular-vector utilization for modal analysis, PUMA)，通过加权最小二乘法求得LP(Linear Prediction)系数，再估计出信号DOA，该算法利用了信号子空间的全部矢量且不需要进行谱峰搜索，因此精度较高，同时算法复杂度较低，但是信噪比较低时性能下降很快。

上述算法均为子空间类算法，其显著缺点为需要已知信号源数作为先验信息，以此来构造信号子空间和噪声子空间。常用的信号源数估计方法有信息论(AIC)准则[12]、最小描述长度(MDL)准则[13]等，但均不适用于相干信号。文献[14]提出了一种无需先验信息的多重Toeplitz矩阵重构 (Multi-Toeplitz, MT)算法，在2M+1个阵元条件下，利用数据协方差矩阵中的M+1行数据构造Toeplitz矩阵，再通过误差最小准则构造代价函数，实现相干信号的DOA估计。该算法不需要构造信号子空间或噪声子空间，因此无需信号源数先验信息，当信噪比较高时，算法性能与子空间类算法的性能相当，但低信噪比条件下性能较差。

针对以上问题，本文提出了一种前后向多重Toeplitz矩阵重构 (Forward and Backward Multi-Toeplitz，FBMT)算法，在MT算法的基础上，构造了后向Toeplitz矩阵，进一步提高了数据利用率。本文算法继承了MT算法无需信号源数先验信息的优点，同时具备更高的测向精度和鲁棒性。

1 信号模型

假设有K个窄带远场信号入射到2M+1个阵元组成的均匀线阵上，信号到达角为{θ1,θ2,…,θK}，且满足K≤2M+1，相邻的阵元间距d等于半波长λ。其中前P个信号是相干信号，剩下的K-P个信号相互独立。不妨设第一个信号s1(t)为直射信号，则第p个相干信号可以表示为

sp(t)=ρps1(t),p=2,…,P

(1)

式中，ρp是第p个相干信号的相干系数。阵列接收数据可以表示为

(2)

式中，a(θi)=[ej2πMdsin(θi)/λ,…,1,…,e-j2πMdsin(θi)/λ]T，i=1,…,K是导向矢量，N(t)表示2M+1维零均值高斯白噪声，噪声功率为σ2。将上式写成矩阵的形式

X(t)=A(θ)S(t)+N(t)

(3)

式中，A(θ)=[a(θ1),…,a(θK)]∈(2M+1)×K表示阵列流形，S(t)=[s1(t),…,sK(t)]T∈K×1表示信号矢量，(·)T表示转置。

2 算法流程

2.1 构造前后向Toeplitz矩阵

首先计算数据协方差矩阵RX=E{X(t)XH(t)}，其中(·)H表示共轭转置。由式(3)可得

A(θ)E{S(t)SH(t)}AH(θ)=

A(θ)RSAH(θ)

(4)

当入射信号中含有相干信号时，信号协方差矩阵RS将会出现秩损，造成信号子空间的能量泄露，此时，传统的MUSIC算法和ESPRIT算法将失效。选取数据协方差矩阵RX中的第m行

rm=[r(m,-M),r(m,-M+1),…,r(m,M)]=

[e-j2πmdsin(θ1)/λ,e-j2πmdsin(θ2)/λ,…,e-j2πmdsin(θK)/λ]RSAH(θ)=

cmAH(θ)

(5)

式中，1≤m≤M+1，cm=[e-j2πmdsin(θ1)/λ,e-j2πmdsin(θ2)/λ,…,e-j2πmdsin(θK)/λ]RS为1×K维行向量，由于信号协方差矩阵RS中不存在全零列，因此cm中不存在零元素。再用长度为M+1的滑窗截取rm中的元素，得到行向量

rm,i=[r(m,-i),r(m,1-i),…,r(m,M-i)]

i=0,…,M

(6)

取第一个行向量rm,0

(7)

(8)

式中，IM+1,m是一个(M+1)×(M+1)维矩阵且第m条对角线元素全为1，其余对角线元素为0。diag(·)为对角化操作，φ=diag([e-j2πdsin(θ1)/λ,…,e-j2πdsin(θK)/λ])为K×K维对角阵，pm=diag(cm)表示矩阵重构之后的伪信号协方差矩阵。由于cm中不含有零元素，因此pm是满秩对角阵，即通过重构矩阵Rm可以消除信源的相干性。

若不考虑噪声的影响，式(8)可以写成

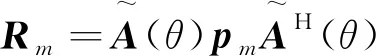
(9)

(10)

式中，J∈(M+1)×(M+1)为置换矩阵，易知因此后向矩阵中含有新的信息。又因为与Rm具有相同的结构，因此可以同时利用前向Toeplitz矩阵Rm和后向Toeplitz矩阵来估计信号的DOA。

2.2 DOA估计

根据文献[14]所提算法，进行代价函数构造以及DOA估计。对于第k个信号，必存在ek∈M+1和其余K-1个导向矢量张成的子空间正交，即

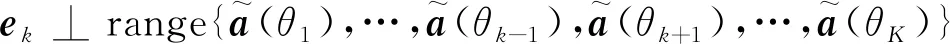
(11)

式中，range{·}表示张成的子空间。用Rm左乘ek可得

(12)

(13)

考虑噪声影响，式(13)可以写成

(14)

(15)

(16)

令

(18)

(19)

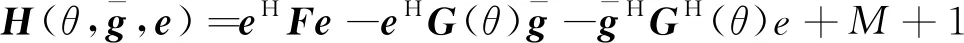
(20)

(21)

式(21)的根为

(22)

将式(22)带入式(16)可得

(23)

(24)

式中，λi表示第i个特征值，有λ1≥…≥λM+1，ui为λi对应的特征向量，因此可以得到

(25)

H(θ)=M+1-maxeig{GH(θ)F-1G(θ)}

(26)

式中，maxeig{·}表示取最大的特征值。

最后构造一个关于θ的空间谱

(27)

Q(θ)谱峰对应的角度即为估计的信号DOA。

2.3 本文的算法流程

Step3： 根据式(18)和式(19)计算矩阵F和矩阵G(θ)；

Step4： 根据式(27)计算空间谱Q(θ)，并通过谱峰搜索得到信号的DOA。

3 复杂度分析

针对文献[14]的MT算法和本文提出的FBMT算法进行算法复杂度分析。两种算法所进行的操作步骤是相同的，算法复杂度主要集中在计算RX，F，G(θ)以及Q(θ)上，下表给出了两种算法的复杂度对比，其中阵元数为2M+1，快拍数为N。

表1 MT算法与FBMT算法的复杂度对比

由表1可知，FBMT的算法复杂度近似是MT的2倍，在数量级上没有大幅的增加。设置仿真条件如下：5个阵元，3个到达角信号，信噪比为15 dB，快拍数为500，进行1000次蒙特卡罗实验，得到MT算法的平均用时为0.0243 s，FBMT算法的平均用时为0.0369 s，运算时间增加了约0.01 s，在可接受的范围内。下文的仿真将表明，改进算法在提高了原算法精度的基础上，一定程度也增加了其可测角数，因此通过增加一部分计算量来获取性能的提升是有价值的。

4 仿真校验

本节通过仿真实验将本文算法与FOSS算法、FBSS算法以及MT算法进行比较，对不同条件下的均方根误差RMSE以及测向成功率PR进行了分析(假设当测向偏差之和小于1°时，测向成功)。在仿真实验中，设信号为零均值高斯信号，噪声为零均值高斯白噪声，由于FOSS、FBSS算法需要信号源数先验信息，而MT算法和本文算法无需先验信息，为方便比较，假设信号源数先验信息都是已知的。均方根误差通过1000次蒙特卡罗实验得到，可表示为

(28)

实验1：相干信号测向能力比较

假设有三个信号入射到5个阵元组成的均匀线阵上，信号到达角分别为[-16°,5°,34°]，快拍数N=500，SNR=15 dB。分别在相干及非相干条件下，利用FOSS、FBSS、MT以及本文算法进行DOA估计，得到的归一化空间谱如图1所示。

图1 归一化空间谱

图中三条红色竖线表示真实信号的DOA，图1(a)显示的是相干信号的归一化空间谱，相干系数分别为[1,0.8ejπ/3,0.5ejπ/4]，可以看出FBSS算法和本文算法均能形成三个尖锐的谱峰，MT算法只能形成两个峰，而FOSS算法受限于阵列孔径，将无法分辨相干信号。由此可知，当阵元数较少时，FBSS算法的谱峰最尖锐，本文算法次之，MT算法出现漏角，而FOSS算法彻底失效。图1(b)显示的是非相干信号的归一化空间谱，此时FOSS和FBSS均不用进行空间平滑，退化为MUSIC算法，可知当信号为非相干信号时，FOSS和FBSS的空间谱相同，MT算法和本文算法的空间谱相近，FOSS和FBSS的谱峰比MT算法和本文算法的谱峰尖锐。需要指出的是本文算法和MT算法均不需要信号源数先验信息，这在一定程度上弥补了其谱峰不够尖锐的缺点。

实验2：不同信噪比条件下的算法性能比较

在实验2中，共有三个信号入射到7个阵元组成的均匀线阵上，信号到达角分别为[-40°,-10°,20°]，快拍数N=300，前两个信号为相干信号，相干系数分别为[1,0.9ejπ/3]，第三个信号独立于前两个信号。信噪比变化范围为-5到15 dB，在不同信噪比条件下进行实验，得到算法性能随信噪比变化如图2所示。

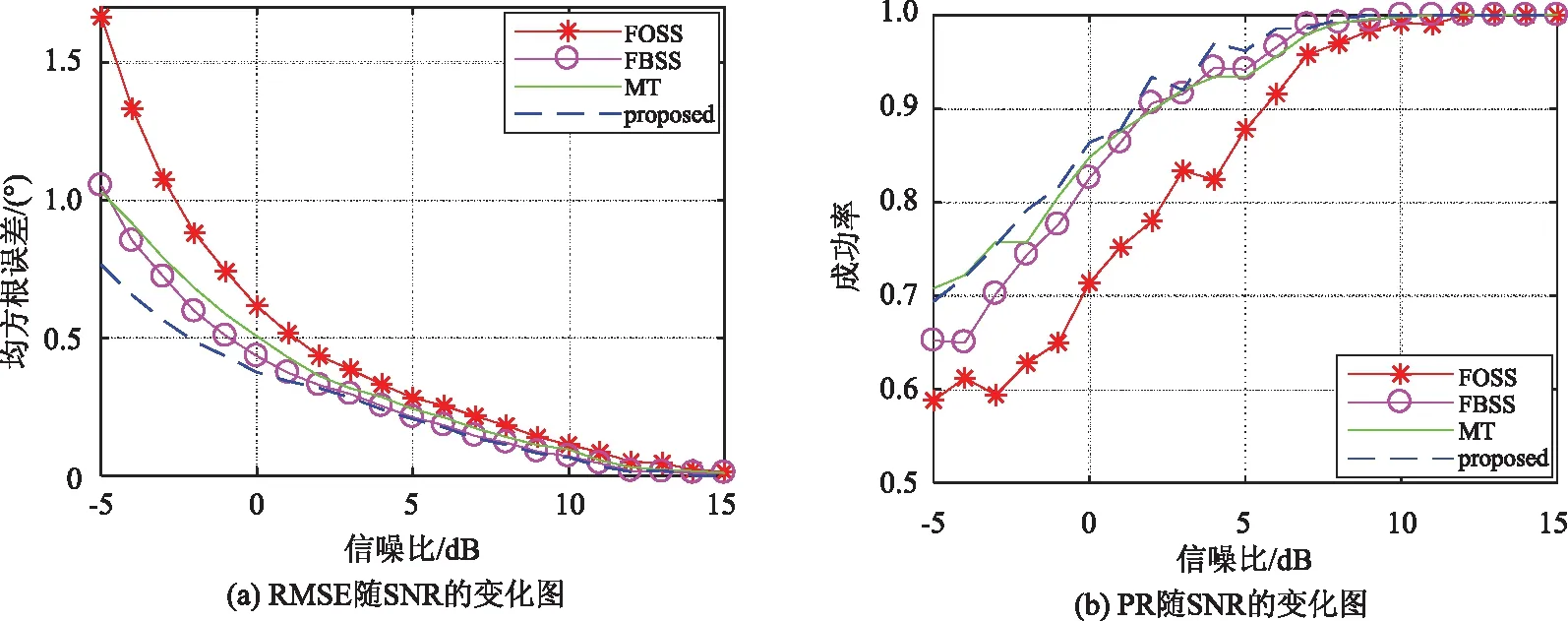
图2 RMSE和PR随SNR的变化图

图2(a)显示的是四种算法的RMSE随着SNR的变化情况，由图可知本文算法的性能最好，FOSS算法的性能最差。图2(b)显示的是四种算法的PR随着SNR的变化情况，当SNR>-3 dB时，本文算法的成功率始终高于其他三种算法，当SNR>5 dB时，四种算法的成功率接近100%。

实验3：不同采样点条件下的算法性能比较

实验3的信号入射条件、阵元条件与实验2一致，且SNR=0 dB，采样点变化范围为100到1000，在不同的采样点条件下进行实验，得到算法性能随采样点变化如图3所示。

图3 RMSE和PR随采样点数的变化图

图3(a)显示的是四种算法的RMSE随着采样点数的变化情况，由图可知本文算法的均方根误差最小，FBSS算法性能略差于本文算法，但好于FOSS算法和MT算法。图3(b)显示的是四种算法的PR随着采样点数的变化情况，可以看出本文算法的成功率在不同采样点数条件下始终略高于其他三种算法，其中MT算法与本文算法成功率相近，均好于FBSS算法和FOSS算法。

5 结 语

针对空间平滑类算法需要信号源数先验信息、MT算法在低信噪比条件下精度不高的问题，本文提出了一种基于前后向多重Toeplitz矩阵重构的FBMT算法，其数据利用率更高，因此估计精度更高、鲁棒性更好，并且在低信噪比、低采样条件下仍然具有较好的性能。