向量优化中基于改进集下真有效解的非线性标量化

白 霞,李 飞

(内蒙古大学 数学科学学院,内蒙古呼和浩特 010021)

§1 引言

近似解在最优化理论和应用中一直占有重要地位.自1979年文献[1]中首次提出向量优化问题近似解概念以来,各种近似解理论已获得大量的成果.向量优化问题的有效解集通常可能会包含某些异常类型的解,因此需要提出各种真有效解来强化有效解集.到目前为止已提出很多真有效解概念,常见的真有效解包括Geoffrion真有效解[2],Benson真有效解[3],Borwein真有效解[4],Henig真有效解[5]等等.文献[6]中引入了改进集并利用改进集提出了E-有效解的概念.近年来,在向量优化中有很多关于改进集的研究,这方面详细成果可见文献[7-12].文献[13]中利用改进集引入了一种新的真有效解,称之为E-Benson真有效解,它统一了某些真有效解和近似真有效解.文献[13]中同时得到了关于E-Benson真有效解的线性标量化的一些刻画.文献[14]和文献[15]分别利用Gerstewitz泛函和基于锥K上的定向距离函数∆−K对E-Benson真效解进行非线性标量化刻画.文献[16]中利用回收锥引进了一种新的真有效解,称之为广义EBenson真有效解,并利用择一定理建立广义E-Benson真有效解的线性标量化定理.文献[17] 中利用Gerstewitz泛函和基于锥K上的定向距离函数∆−K等两类非线性标量化函数及其相应非凸分离定理给出广义E-Benson 真有效解的一些非线性标量化性质.受文献[14-17]启发,本文通过基于改进集E的Gerstewitz泛函ϕq,E及定向距离函数∆−E分别建立了E-Benson真有效解和广义E-Benson真有效解的非线性标量化结果.同时文中还举例说明了部分结果.

§2 预备知识

其中inf ∅=+∞.

当Gerstewitz泛函ϕq,G中G是一般集合时,其主要性质包括非线性分离性质见文献[18].在向量优化很多应用中通常集合G取为闭凸锥K.赵克全等人在文献[14]中及本文中均将集合G取为改进集E.

引理2.1设E是Y中关于K的改进集且满足E+(0,∞)q ⊂intE,q ∈intE,则函数ϕq,E是连续的且满足

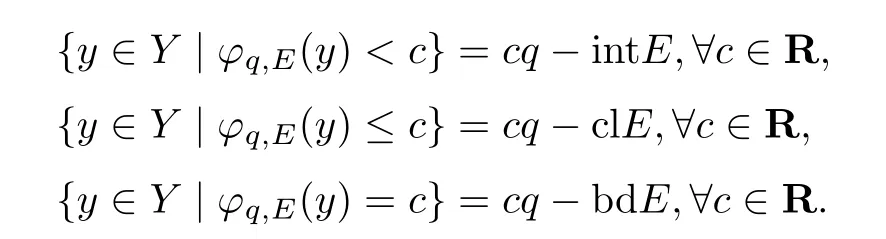
证根据文献[18]中定理2.3.1,可得结论成立.

Zaffaroni在文献[19]中提出了另一个非线性标量化函数即定向距离函数.

设A是赋范线性空间Y中的集合,∆A(y):Y −→R∪{±∞}定义为

其中d∅(y)=+∞,dA(y)=‖z −y‖.

∆A函数的很多良好性质可参考文献[19].本文基于改进集E的∆E函数性质如下.

引理2.2(见[20]) 设E是Y中关于K的改进集且非空,则

(1)∆E是实值且是1-Lipschitz的;

(2)clE={y ∈Y:∆E(y)≤0},bdE={y ∈Y:∆E(y)=0},YE={y ∈Y:∆E(y)≥0},intE={y ∈Y:∆E(y)<0};

(3)若E是凸的,则∆E是凸的;

(4)若E是锥,则∆E是正齐次的.

注2.1据文献[21]中引理3.3知,若E是Y中关于K的改进集且E ⊂K,则E是co-radiant集.再由其定理3.1可得,若E是凸的则∆E是次可加的.

§3 Gerstewitz泛函ϕq,E关于真有效解的非线性标量化

考虑数值优化问题

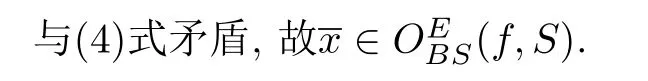
注3.1文献[8,14]中定义函数ϕq,E时将q取值于锥K中,在证明集合int(E ∩K)∅后,分别对E-有效解与E-Benson真有效解标量化刻画时取定q ∈int(E ∩K).而本文在定义函数ϕq,E时将q取值于改进集E中,对E-Benson真有效解标量化刻画时取定q ∈int(EK),故在函数ϕq,E中q的取值不再依赖于锥K.

利用Gerstewitz泛函ϕq,E还可以对广义E-Benson真有效解进行非线性标量化刻画,得到下面推论3.1和推论3.2.证明过程与定理3.1,定理3.2相似,这里省略.

§4 定向距离函数∆−E关于真有效解的非线性标量化

本节利用基于改进集E的非线性标量化函数∆−E给出向量优化问题(VP) 的E-Benson真有效解的非线性标量化定理.本文是把∆函数定义在比锥更一般的集合即改进集E上而进行的非线性标量化刻画,这与文献[15]将其定义在锥K上不同.本节中始终假设Y是赋范线性空间.

考虑数值优化问题

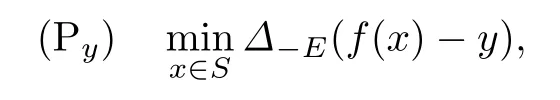
其中y ∈Y.问题(Py)的ε-近似解全体所构成集合记为AMin(∆−E(f(x)−y),ε),严格ε-近似解全体所构成集合记为SAMin(∆−E(f(x)−y),ε).

注4.1文献[8,15]是把∆函数定义在锥K上,利用函数∆−K分别刻画E-有效解与E-Benson真有效解的非线性标量化特征.而本文是把∆函数定义在比锥更一般的集合即改进集E上,利用函数∆−E对E-Benson真有效解进行的非线性标量化刻画,因此是把∆函数推广到更一般的集合上而得到的结果.

利用∆−E还可以对广义E-Benson真有效解进行非线性标量化刻画,得到下面推论4.1和推论4.2.证明过程与定理4.1,定理4.2相似,这里省略.