长相依面板数据的斜率变点分析

朱 旭,庞天晓

(浙江大学 数学科学学院,浙江杭州 310058)

§1 引言

许多经济和金融时间序列的数据都具有单变点或者多变点的特征,参见Bai和Perron[1],Hansen[2],Lee等[3],以及Perron和Zhu[4].此外众所周知,经济和金融数据往往还具有长相依的特征.例如日元兑美元的汇率数据被广泛认为存在长相依,参见Horv´ath和Kokoszka[5].因此在处理实际数据时,往往面临结构变点和长相依同时存在的情形.例如Jaruˇskov´a[6]在非平稳的长周期的水文数据中发现了长相依的证据,同时认为数据中存在结构变点.大量的研究表明,长相依的存在会使传统的变点理论失效.因此对长相依数据进行变点分析既具有理论意义,也具有实际意义.

有相当多的文章研究了长相依时间序列中的结构变点.例如Kuan和Hsu[7]研究了均值变点并给出了估计量的收敛速度.Chang和Perron[8]研究了参数为d的分整(fractionally integrated)过程中的斜率和均值变点,并给出了估计量的收敛速度和极限分布.Perron和Qu[9]提出用周期图来研究股票指数回报的波动率,发现存在长相依和均值漂移.Shao[10]提出一种检验流程来检验长相依时间序列中的均值变点.Iacone等作者[11]提出一种检验流程来检验参数为d的分整时间序列中的斜率变点.

面板数据中存在公共变点的现象在实际生活中非常普遍.例如税收政策的变化可能会影响每个人的收入.另一个著名的例子是2008年发生的全球金融危机几乎影响了所有国家的GDP(Gross Domestic Product)数据和资本市场表现,并带来一定时间内持续的影响.类似地,新的科学技术的诞生,新药的研发生产,以及政府层面新的政策措施都会对经济社会造成或多或少的影响.

结构变点从时间序列的研究延申到面板数据的研究可以追溯到1990年.Joseph和Wolfson是最早的一批研究面板数据中的结构变点的学者[12-13],他们提出了N个面板上存在独立同分布的N个变点的随机变点模型,并给出了变点分布的相合估计量.不久后随机变点模型被Joseph等[14]推广到了自回归模型.Bai[15]利用最小二乘的方法估计了面板数据中的公共均值变点,同时证实了变点估计量是相合的,这与平稳时间序列中变点估计量是不相合的结论截然相反.值得一提的是,以上文章中的面板数据都是假设横截面独立的.此后,面板数据中的公共变点研究得到了计量经济学界和统计学界的大量关注,横截面独立的面板数据模型也在一些文章中被推广到了横截面相依情形.例如,Horv´ath和Huˇskov´a[16]研究了存在横截面相依的面板数据中公共均值变点的检验问题,Kim[17-18]研究了横截面相依的面板数据中存在斜率变点以及斜率与截距变点同时存在时的变点估计问题,Li等作者[19]利用自适应group fused LASSO惩罚的主成分方法估计横截面相依的面板数据中的变点,Qian和Su[20]提出了横截面相依面板数据中的公共变点的收缩估计量,Baltagi等作者[21-22]提出了CCE(common correlated effects)估计量并把它应用于横截面相依面板数据中变点的研究,Westerlund[23]采用了基于CCE的方法对时间长度固定的横截面相依面板数据中的变点进行研究.值得注意的是,大部分现有的文献都假设面板数据在时间维度上是弱相依的,研究长相依面板数据中的结构变点的文章相对较少.

本文假设面板数据具有横截面的相依性,同时每个时间序列都是长相依的(记忆参数d ∈(0,0.5))且带有斜率变点.这种模型在宏观经济和金融中具有广泛的应用.用最小二乘的方法估计斜率变点发生的时刻以及发生时刻的分数,并研究了当(T,N)(T表示时间长度,N表示个体数)联合趋于无穷时估计量的渐近性质: 估计量的相合性,收敛速度以及极限分布.得到了一些有趣的结论: 大部分情况下斜率变点估计量的收敛速度随着记忆参数d的增大而减缓,但当T和N满足T2d=o(N),且公因子与变点的变化幅度存在交互效应时,变点时刻估计量的收敛速度仅与T有关.

本文结构如下:§2给出模型的具体形式以及一些假设,§3介绍变点估计量的渐近性质,§4给出Monte Carlo模拟结果,用于评估变点估计量在有限样本情形下的表现,§5对论文进行了总结,文章中的理论证明放在§6.

§2 模型与假设

首先介绍本文接下来需要用到的一些记号.“⇒”表示概率测度弱收敛(参见Billingsley[24]),“”表示依概率收敛,“”表示依分布收敛,“iid”表示独立同分布,aTbT表示存在两个正常数c1和c2使得对于所有足够大的T,c1≤aT/bT ≤c2成立,其中aT和bT是两个关于T的取值恒为正的函数.设D[0,1]是[0,1]上的函数空间,且是存在左极限和右连续的Skorohod拓扑.对于矩阵A,记‖A‖=[tr(A′A)]1/2,其中tr[·]表示矩阵的迹.此外用M表示正常数,它的取值与T和N无关,但在不同的地方可取不同的值.除非另有说明,本文中的极限均理解为(T,N)→∞,即T和N联合趋于无穷.

本文研究的面板数据模型为

注假设1是为了保证变点的可识别性,是变点研究领域中的常见假设.假设2(1)假设公因子是一个线性过程并可以应用泛函中心极限定理(参见Phillips和Solo[26]).假设2(2)假设误差ei,t在时间维度上是长相依的,但其方差在横截面维度上可以不同.假设2(3)是一个技术性假设,是为了应用面板数据的联合中心极限定理(参见Phillips和Moon[27]).假设2(4)假设公因子和模型误差是相互独立的.假设3和4描述了模型的总体变点强度,公因子的强度,以及变点的变化幅度与公因子之间的相互影响程度.

§3 极限性质

本节介绍估计量ˆT1的极限性质.后文中,所有的Op(·)将按照其严格的定义理解,即随机变量不会是op(·).

定理3.1若假设1-4成立,当(T,N)→∞,d ∈(0,0.5)时,有下面的结论.

注以上结论都表明变点估计量是相合的.结论(1)说明在不存在横截面相依时,收敛速度与记忆参数d,T和N有关,且d越大收敛速度越慢,这与直觉吻合,因为d ≥0.5时时间序列将变成非平稳.结论(2)说明当AHγ/0时,即公因子与变点的变化幅度存在交互效应,如果个体数N相对于时间长度T并没有足够大时,收敛速度依然由d,T和N共同决定,且随着d的增大而变慢.结论(3)说明当T2d=o(N),即个体数N相对于时间长度T足够大时,的收敛速度仅与T有关.

有了收敛速度,接下来推导估计量的极限分布.有下面的定理.

定理3.2若假设1-4成立,当(T,N)→∞,d ∈(0,0.5)时,有下面的结论.

注以上的三个结论表明: 当变点分数的真值λ0越接近中间值1/2,或者斜率变点的信号强度越大(即Aγγ越大),则渐近分布的方差越小.

§4 数值模拟

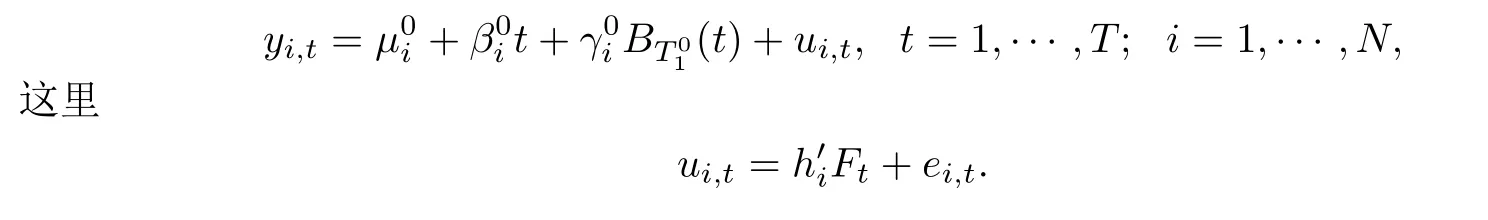
在这一节,将通过Monte Carlo模拟来评估估计量在有限样本情形下的表现.对所有实验,重复次数都为2000次.数据由以下过程产生.设公因子Ft是一维的且满足Ft=0.2Ft−1+wt,F0=0,wt独立同分布于N(0,1);一维因子载荷hi有两种情况: 若不存在横截面相依,则对所有的i取hi=0,若公因子与变点的变化幅度存在交互效应,即AHγ/0,设hi由U(0,1)随机生成;参考McLeod和Hipel[28]以及Hosking[29]的方法,随机生成N个长相依时间序列{ei,t,t=1···,T},i=1,···,N,使得(1−L)dei,t=εi,t,εi,t=σiηi,t,其中σi由U(1,1.5) 随机生成,{ηi,t,t ≥1,i ≥1}独立同分布于N(0,1),记忆参数根据具体情况从d ∈{0.05,0.1,0.25,0.4,0.45}中选取.为方便起见,设定==0,因为这些参数的大小并不会影响Monte Carlo模拟的结果,影响模拟结果的是斜率的变化幅度.设由U(0,0.3)随机生成.此外,设定变点时刻的真值=0.5T,以及π=0.05.接下来,用直方图的形式来评估在定理3.1中的表现.

图1展示了(T,N)∈ {(100,10),(100,40),(200,10),(200,20)},d ∈ {0.1,0.25,0.4},所有的hi=0时,的直方图.横向比较第一行可以看出估计量的估计误差随记忆参数d的增大而增加;依次纵向比较可以看出固定d时估计误差随T和N的增大而减小,这与定理3.1(1)的结论相符.图2展示了(T,N)∈{(200,10),(200,20),(400,10),(400,20)},d ∈{0.25,0.4,0.45},公因子与变点的变化幅度存在交互效应时,的直方图,这些T,N,d的设定是为了保证N=o(T2d)或T2d N能够被满足.同样通过横向和纵向的比较,可以看出这与定理3.1(2)中的结论相符.图3则展示了(T,N)∈{(40,100),(40,200),(100,100),(100,200)},d ∈{0.05,0.1,0.25},公因子与变点的变化幅度存在交互效应时,的直方图,这些T,N,d的设定是为了保证T2d=o(N)能够被满足.横向比较第一行可以看出变点估计量的估计误差与d无关,纵向比较第一列可以看出估计误差与N亦无关,纵向比较第二和三列则可看出变点估计量的估计误差与T有关,T越大估计误差越小.以上模拟结果与定理3.1(3)中的结论相符.

图1 当所有的hi=0,且N=o(T3−2d)时,的直方图

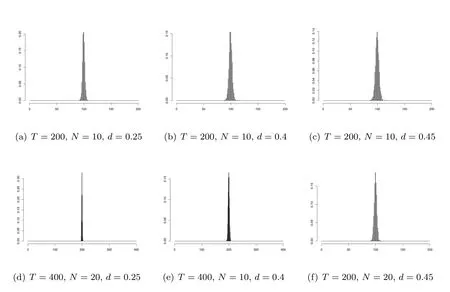
图2 当AHγ0,且N=o(T2d)或T2d N时,的直方图

图3 当AHγ/0,且T2d=o(N)时,的直方图

最后比较估计量的有限样本分布与定理3.2的极限分布.图4和图5展示T1/2−dN1/2()在不存在横截面相依和公因子与变点的变化幅度存在交互效应这两种情况下,估计量的有限样本分布与极限分布.可以看出d越小,有限样本分布与极限分布的逼近效果越好.其次,对于相同的N和d,不存在横截面相依的情况下有限样本分布更接近极限分布(即使T更小),这说明公因子的存在会影响估计量的有限样本分布.图6展示了当公因子与变点的变化幅度存在交互效应,且N/T2d收敛到不为零的常数时,T1/2−dN1/2(−)的有限样本分布与极限分布.可以看出,两者的吻合程度较高.最后,图7展示了当公因子与变点的变化幅度存在交互效应且T2d=o(N) 时,T1/2()的有限样本分布与极限分布.可以看出,有限样本分布与极限分布的吻合度与N和d的关联较小,但当T变大时,有限样本分布更接近极限分布.这些模拟结果与定理3.2(3)中的结论相符.

图4 当所有的hi=0,且N=o(T3−2d)时, T1/2−dN1/2( −)的有限样本分布和极限分布

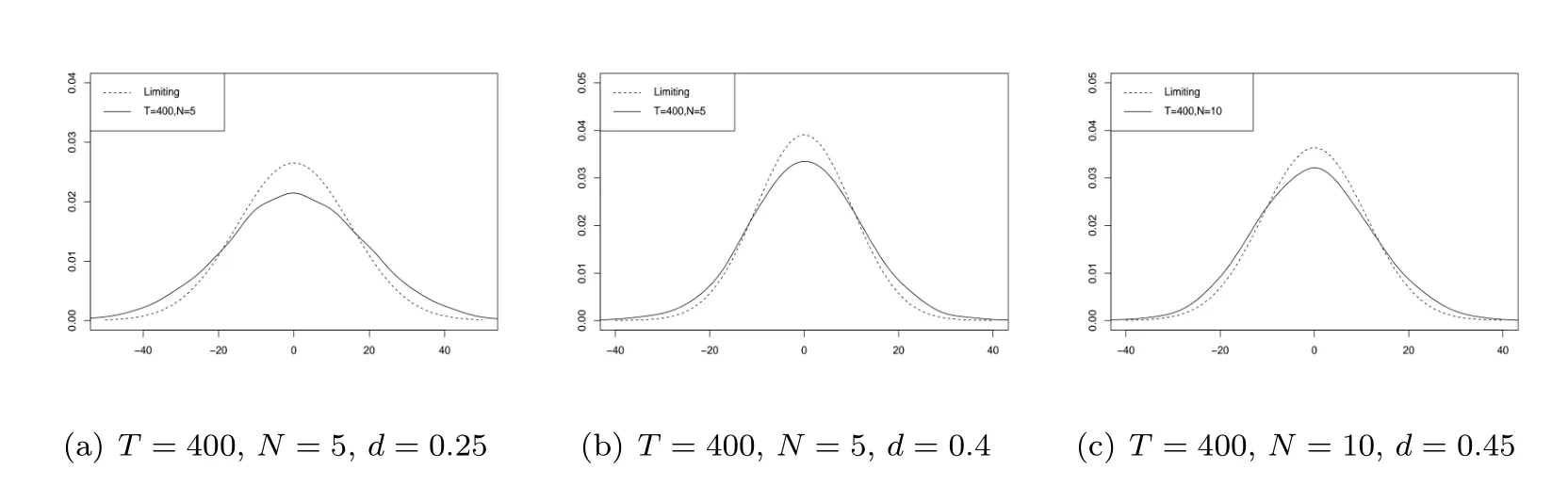
图5 当AHγ 0,且N=o(T2d)时, T1/2−dN1/2( −)的有限样本分布和极限分布

图6 当AHγ 0,且N/T2d收敛到不为零的常数时, T1/2−dN1/2( −)的有限样本分布和极限分布

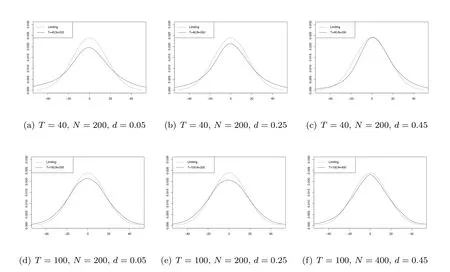
图7 当AHγ0,且T2d=o(N)时, T1/2−dN1/2( −)的有限样本分布和极限分布

§5 结论

本文研究了面板数据同时存在结构变点,时间序列长相依以及横截面相依的变点估计问题.用最小二乘的方法估计了变点发生的时刻,并讨论了估计量的相合性,收敛速度以及极限分布.本文的结论表明在不存在横截面相依时,变点时刻的估计量的收敛速度与记忆参数d,时间序列长度T以及个体数N有关,且d越大收敛速度越慢;当公因子与变点的变化幅度存在交互效应,且N相对于T并没有足够大时,收敛速度依然由d,T和N共同决定,并随着d的增大而变慢;然而当T2d=o(N),即N相对于T足够大时,变点时刻估计量的收敛速度将仅与T有关.最后通过Monte Carlo模拟比较了变点估计量的有限样本分布和极限分布,并印证了本文的理论成果.

§6 证 明

由式(9)可知,若对所有i都有hi=0,则SXU仅剩其中的第二项;若不然,还需要比较式(11)和式(14)阶的大小,即比较T2d和N的相对大小.若N=o(T2d),则SXU的阶将由式(9)中的第二项决定;若T2d=o(N),则SXU的阶将由式(9)中的第一项决定;若T2d和N同阶,则SXU的阶将由式(9)整体决定.因此在λ ∈(0,1)上一致地有