周期环境中年龄等级结构种群模型的数值方法
窦艺萌,何泽荣
(杭州电子科技大学 运筹与控制研究所,浙江杭州 310018)
§1 引言
绝大部分生物种群内部的个体之间存在等级或社会地位差异,这已是一种不争的事实,参见综述文献[1]及其所引文献.除了现存的大量生态学研究成果,学者们也基于等级差异为种群建立了一些数学模型,并且作了一些理论和数值分析,以期对这类种群的演化作出合理预测,或者发现一些有趣也有挑战性的科学问题.文[2-11]主要探讨模型的理论问题,包括解的存在唯一性、平衡态的存在性与稳定性,以及解的长时间行为.比较特别的是,文[7]针对一类基于个体尺度的等级结构种群模型,发现了包含Delta函数的解.
除了必要的理论分析工作以外,模型的数值计算也是一个重要的侧面,对于模型的实际应用尤其如此.目前这方面的工作还远不完善.文[10]对一类基于尺度的等级结构模型,提出了近似函数逼近,而文[11]给出了一类基于年龄的等级模型的数值逼近算法,证明其收敛性.文[12-13]针对一类具有边界控制的尺度结构等级模型,分别提出了有限差分和有限体积的WENO方法.
由于季节变化等因素的影响,种群的栖息环境常常发生周期性变化,由此引起个体生命参数发生相应的变化.因此基于周期性个体生命参数的等级结构种群模型是一种重要类型,目前还没有相关的成果报道.本文基于文[14]的理论分析,进一步考虑模型解的数值计算方法.需要强调的是,现有相关工作中所有的数值方法均不适用于本文的模型,因为所采用的模型各有侧重,互不包含.此外,由于本文模型融入了个体迁移因素,且函数参数具有时间周期性,采取的离散化方法在技术细节方面与文[11]有所不同.§2展示本文模型,给出离散化方法;§3严格证明算法的收敛性,§4给出计算实例,§5总结全文.
§2 模型及其离散化格式
假设个体的生存环境及生命参数随时间呈周期性变化,考虑种群模型的数值求解问题
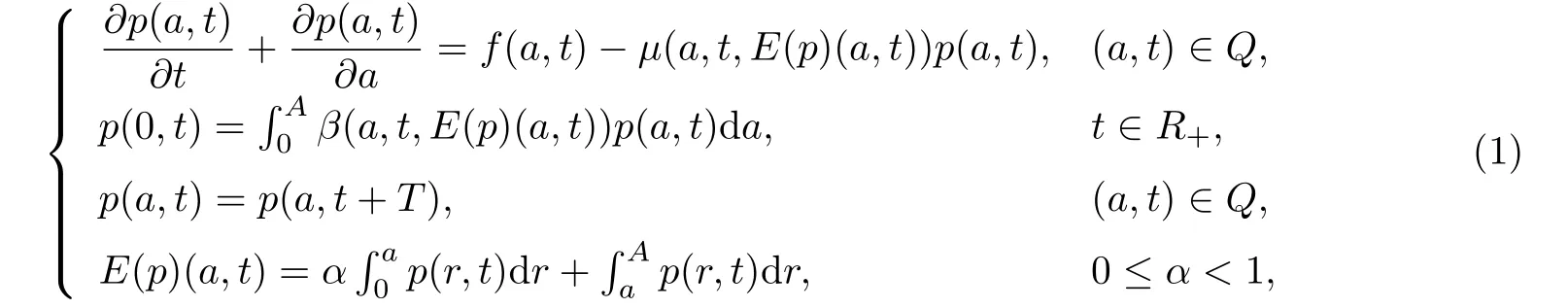
其中R+=[0,+∞),Q=(0,A)×R+;A是种群个体的最大年龄,T为生命参数变化周期.其它状态变量和参数的含义如下:p(a,t)表示t时刻年龄为a的个体密度;f(a,t)是外界向种群生存环境的个体迁入率;E(p)(a,t)表示在t时刻年龄为a的个体所面临的内部环境,其中α代表年龄小于a的个体的等级系数;β(a,t,E(p)(a,t))和µ(a,t,E(p)(a,t))分别表示t时刻年龄为a的个体的繁殖率和死亡率,也依赖于内部环境.
本文的基本假设如下.

(A3) 函数β和µ关于第三个变量满足局部Lipschitz 条件: 即对∀m>0,∃C >0,使得
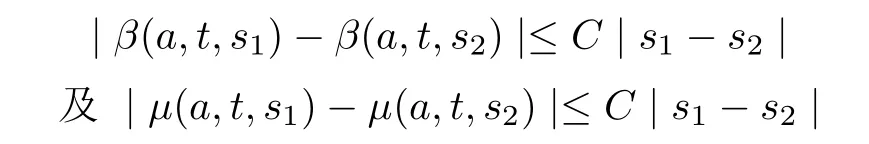
对∀s1,s2∈[0,m],∀(a,t)∈Q均成立.
(A4)f ∈L∞(Q);且对任意(a,t)∈Q,f(a,t)≥0,f(a,t)=f(a,t+T).
注2.1文[14]已经证明: 若假设(A1)-(A4)成立,则模型系统(1)存在唯一的解p(a,t),它在Q上非负有界.
下面给出模型(1)的离散化算法,其中每一个偏导数都被一个具有不同分母(时间或年龄步长)的有限差商所取代.由于解的周期性,不妨先考虑区域[0,A]×[0,T],并对周期解赋予一个初始分布:

设N为一个正整数,令k=T/N表示时间的离散化参数;设正整数M为到达种群最大年龄A的步数,令h=A/M表示年龄的离散化参数.记i为年龄ai=ih,0≤i ≤M所对应的年龄指标,n为时间tn=nk,0≤n ≤N所对应的时间指标.记系统(1)解函数的格点值=p(ai,tn),0≤i ≤M,0≤n ≤N.
以表示对的数值近似,定义
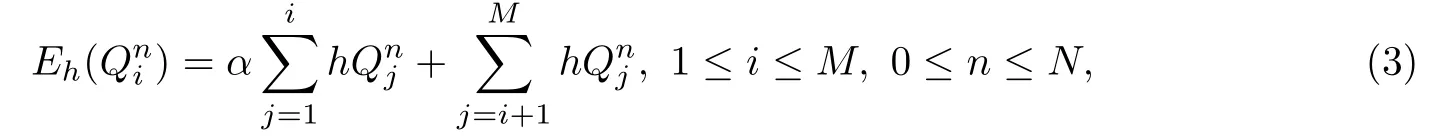
模型(1)可用迎风差分格式
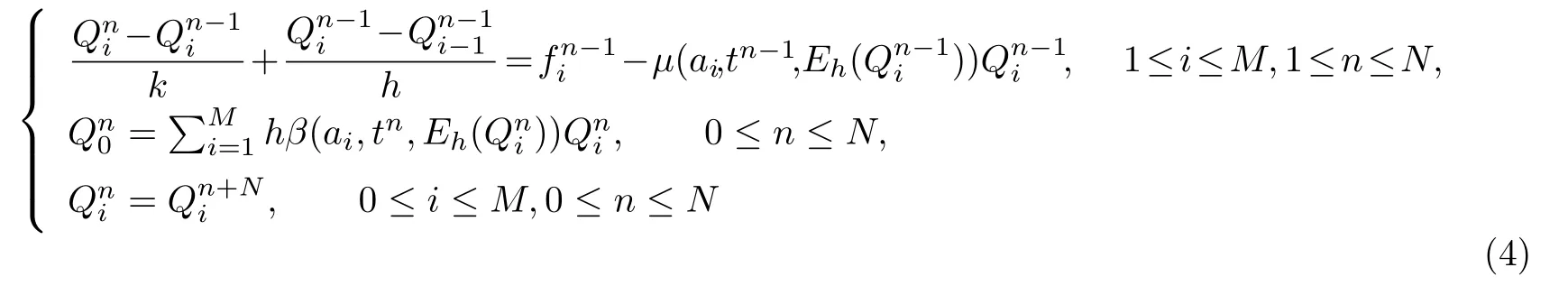
来近似代替.
§3 算法的收敛性
令A′为任一正数,N为自然数集.定义集合H={h>0:h=A′/M′,M′ ∈N}.对∀h ∈H,定义空间
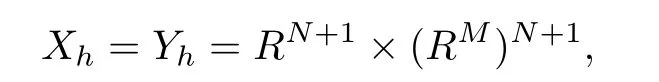
其中Xh用于存储格点处系统(1)解的信息,Yh用于存储差分格式(3)-(4)给出的近似解信息,RN+1代表了N+1 个边界位置(a=0,t=tn),0≤n ≤N;而(RM)N+1则代表其余位置(a=ai,t=tn),1≤i ≤M,0≤n ≤N.为了测量误差大小,在空间Xh,Yh中定义范数

利用上述记号和定义可知:Qh=(Q0,Q0,Q1,···,QN)∈Xh是迎风差分格式(3)-(4)的解,当且仅当它是离散问题

的解.
引理3.1若假设(A1)-(A4)成立,则对充分小的h和k,局部离散误差满足
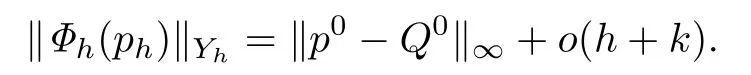
证由(7)-(8)式可知,当h,k →0时,显然有
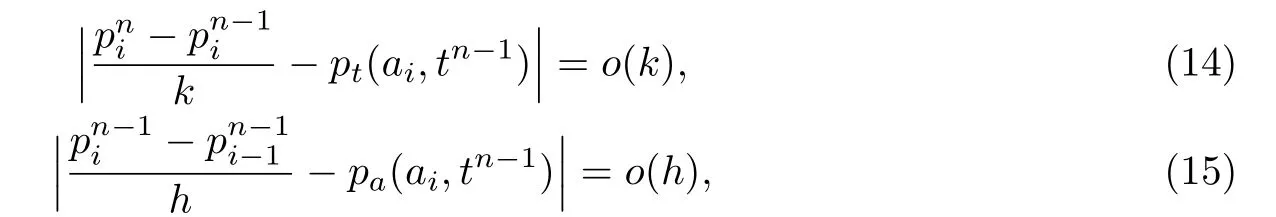
并且这一估计关于i,1≤i ≤M和n,1≤n ≤N一致成立.
另一方面,由假设(A3)可知,对任意0≤n ≤N,
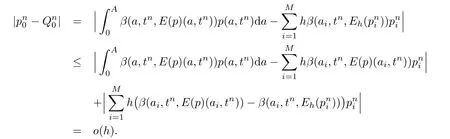
定义3.1[15]若存在两个正常数h0和S,使得∀h ∈H,h ≤h0,∀Vh,Wh ∈B(ph,Mh),有
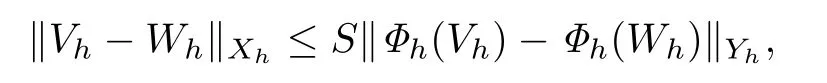
则称离散化映射Φh关于阈值Mh稳定.
引理3.2设Fn,Gn,n ≥0 为非负数列,且满足Fn+1≤(1 +ck)Fn+k(Gn+g),n=0,1,2,···,其中k,g,c均为非负常数,则有
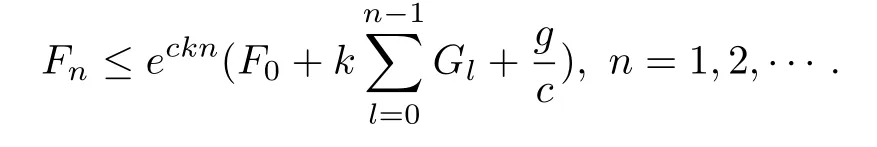
证对任意n ≥1,
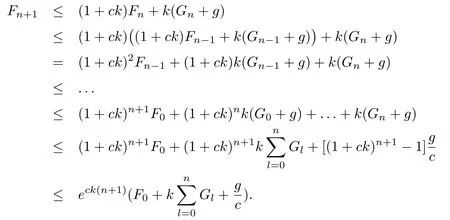
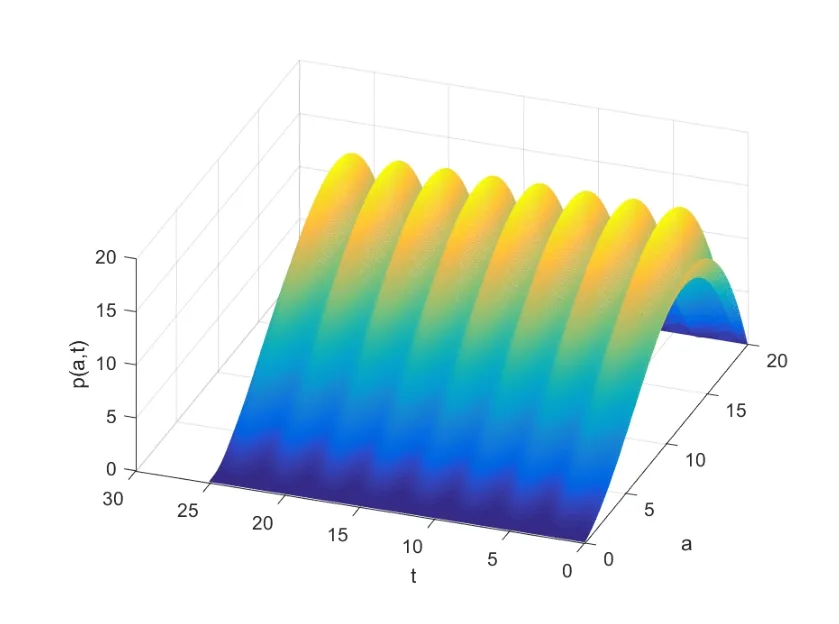
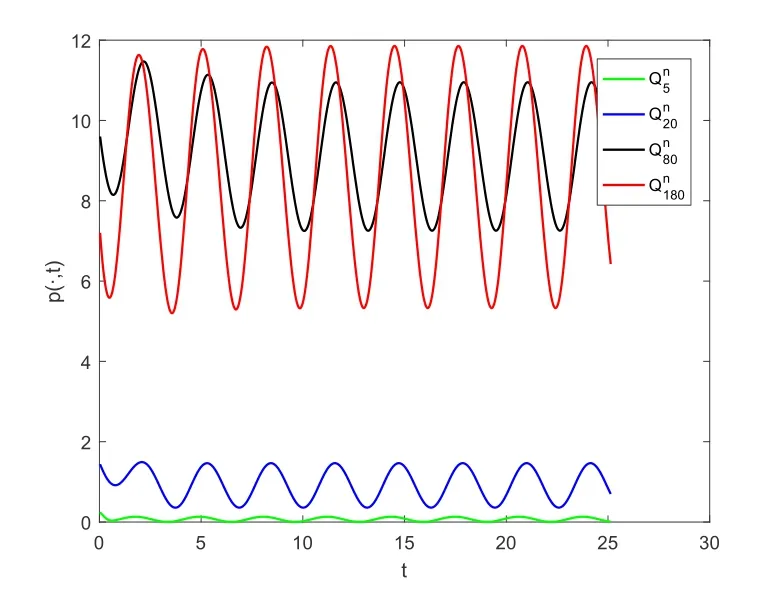
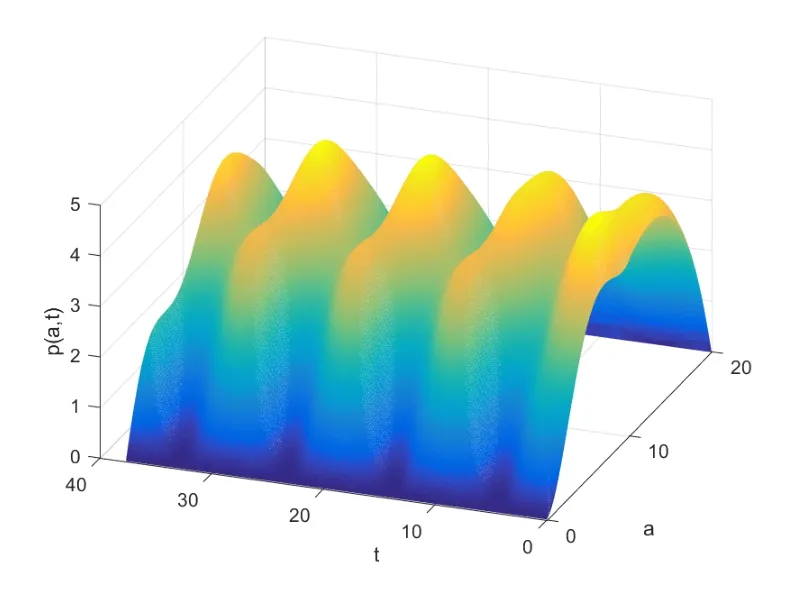
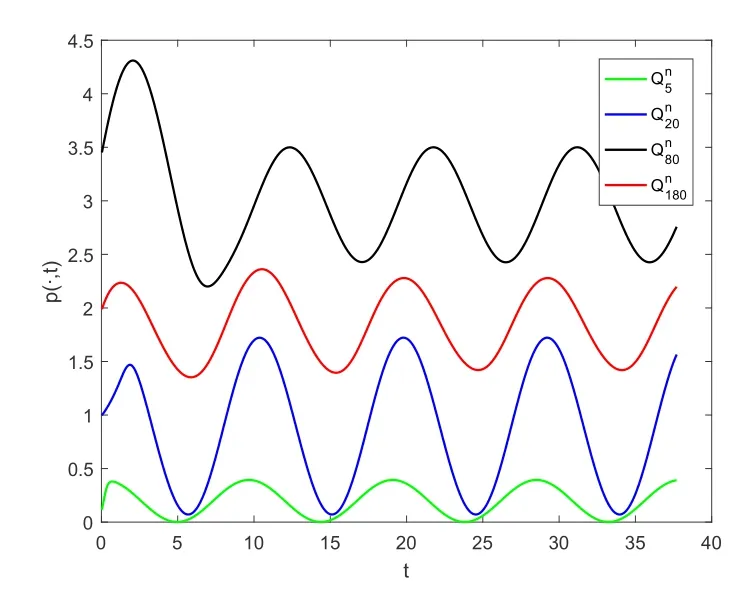
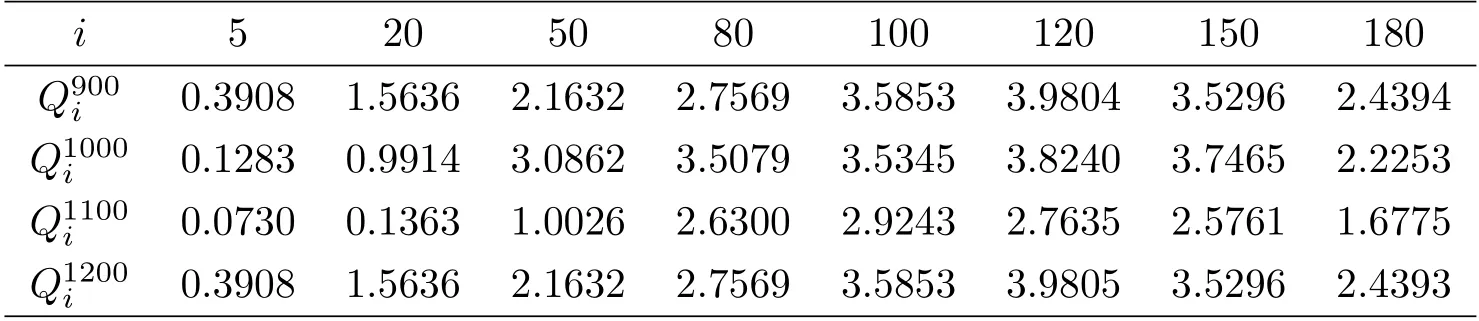
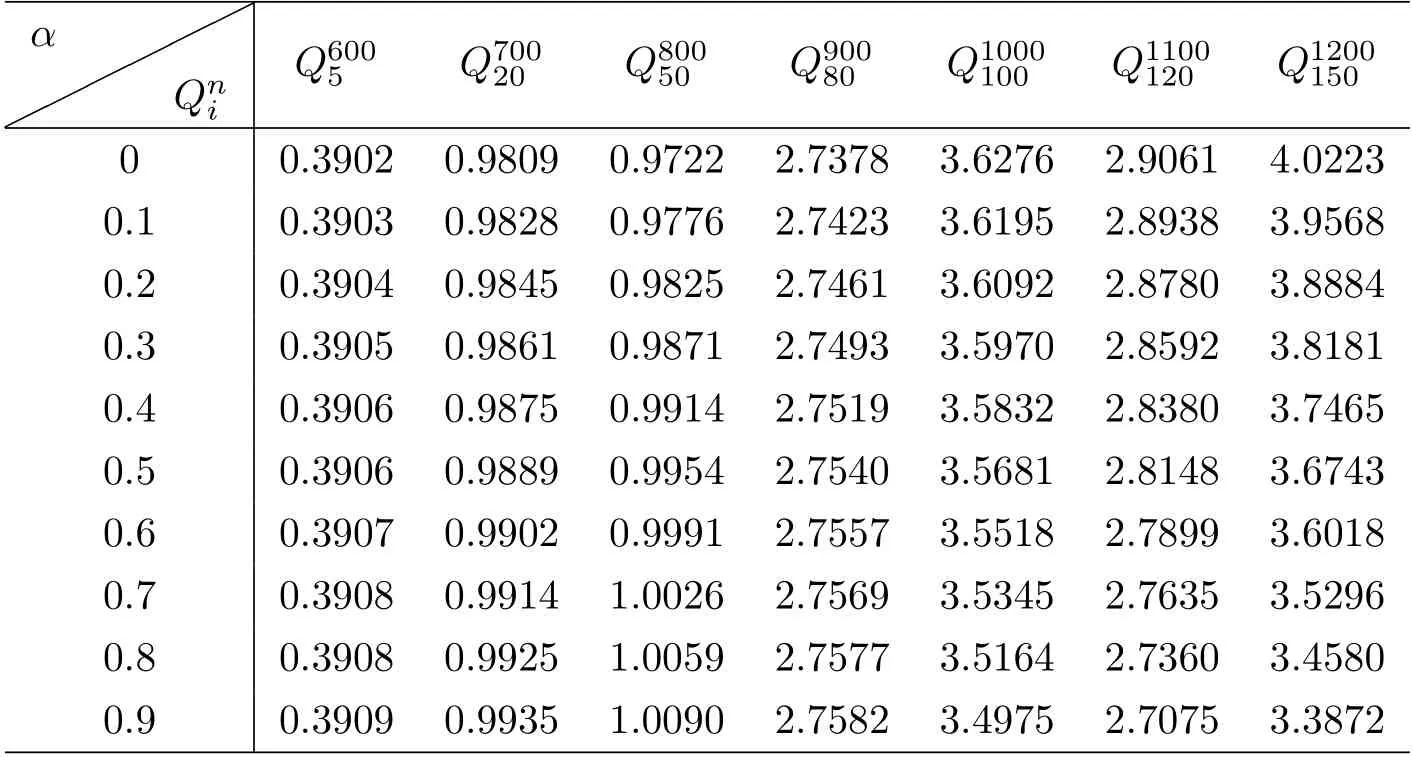
引理3.3若k=rh,0 由于存在阈值Mh,所以一维向量的无穷范数是有界的,即存在一个常数C(下文中的C都代表一个与h,k无关的正数;为表述方便,C在不同地方代表不同的值),使得对任意0≤i ≤M,0≤n ≤N,有 引理3.4[16]若(13)式一致成立,且关于阈值Mh是稳定的;此外Φh在B(ph,Mh)中连续,并满足‖Φph‖Yh=o(Mh)(h →0),则有下述结论成立. 1. 离散化系统(9)-(12)在B(ph,Mh)中存在唯一的解; 2. 当h →0时,结论<1>中的解收敛于原系统(1) 的理论解. 结合引理3.1-引理3.3的结果,得到以下结论. 定理3.1如果(A1)-(A4) 成立,且k=rh,0 注3.1定理3.1表明0 例4.1对于系统(1),选择参数A=20,T=π,α=0.7,h=0.1,k=0.01π.取外界向种群生存环境的迁入率函数为 为模拟种群实际演化情形,设置一定的初始年龄分布函数 根据算法(3)-(4),利用MATLAB进行计算,作出八个周期内的种群密度函数图像,如图4.1所示.除此之外,为直观看出周期性结果,以p(a,t)在a=0.5,2,8,18时为例,分别作出p(a,t)关于t的曲线图,如图4.2所示. 图4.1 种群密度函数 图4.2 密度随t变化的图像 从图中容易看出,历经一段时间的发展后,种群密度p(a,t)随t发生周期性变化.由于无法了解真实情况下某种群在某个时间周期中具体的演化方程,所以设置了一定的初始年龄分布函数,这就导致了图4.2在一开始具有振荡现象.但是在历经一段时间的发展后,种群密度逐渐开进行周期性变化,直观地印证了前述分析结果的正确性. 例4.2对于系统(1),令T=3π.外界向种群生存环境的迁入率函数为 设置种群的初始年龄分布函数 其他参数与例4.1中的相应参数一致. 利用前述离散化算法,可作出四个周期内的种群密度函数图像,如图4.3所示.除此之外,为直观看出周期性结果,以p(a,t)在a=0.5,2,8,18时为例,分别作出p(a,t)关于t的曲线图,如图4.4所示. 图4.3 种群密度函数 图4.4 密度随t变化的图像 同样可看出,在历经一段时间的发展后,种群密度p(a,t)随t进行周期性变化.除此之外,比较图4.1及4.3的两张曲面可以看出: 种群初始分布和外界迁入对密度函数有重要影响. 接下来再考察等级系数α对种群密度的影响.以α=0.7为例,观察例4.2中的一个周期:t ∈[9π,12π].下表4.1中给出α=0.7时,p(a,t)在a=0.5,2,5,8,10,12,15,18和t=9π,10π,11π,12π时的近似值. 表4.1 α=0.7时, p(ai,tn)的近似值 表4.1 α=0.7时, p(ai,tn)的近似值 再取α=0,0.1,0.2,···,0.9时,分别给出种群密度函数在格点(5,600),(20,700),(50,800),(80,900),(100,1000),(120,1100),(150,1200) 处的近似值,如下表4.2所示. 表4.2 α=0,0.1,0.2,···,0.9时, p(ai,tn)的近似值 表4.2 α=0,0.1,0.2,···,0.9时, p(ai,tn)的近似值 观察表4.2不难发现: 随着等级系数α的增加,前4列数值单增,后3列数值单减.这是近似计算结果,从系统模型(1)本身的结构很难看出! 虽然本文模型具有周期型连续年龄结构模型的通常形式,但它允许不同年龄的个体面临不同的种内竞争环境,从而更加接近生态实际,当然也具有更强的非线性.因此,前述算法拓展了一些非线性年龄结构模型的已有算法,比如文[17-19]的方法,以及专著[20]中有关非线性模型的数值计算.另一方面,也应指出: 本文的近似计算方法虽然收敛,但证明过程只保证了一阶精度.如何在确保收敛的前提下,进一步提高计算精度,提升计算效率,仍需作深入研究. 致谢作者感谢审稿专家对原稿的仔细审读和宝贵建议.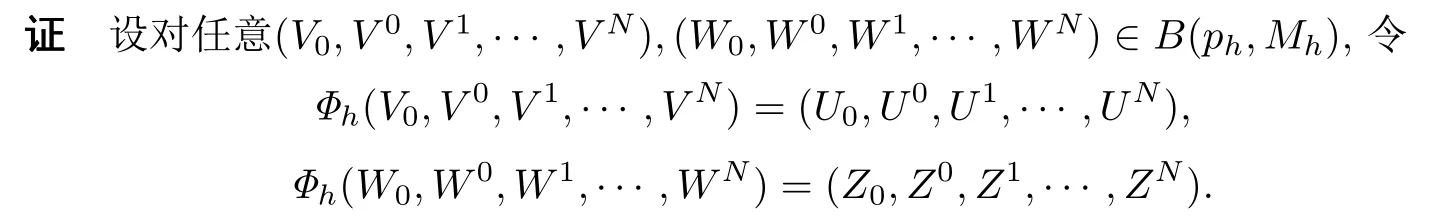

§4 数值实验
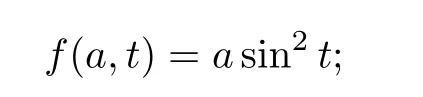
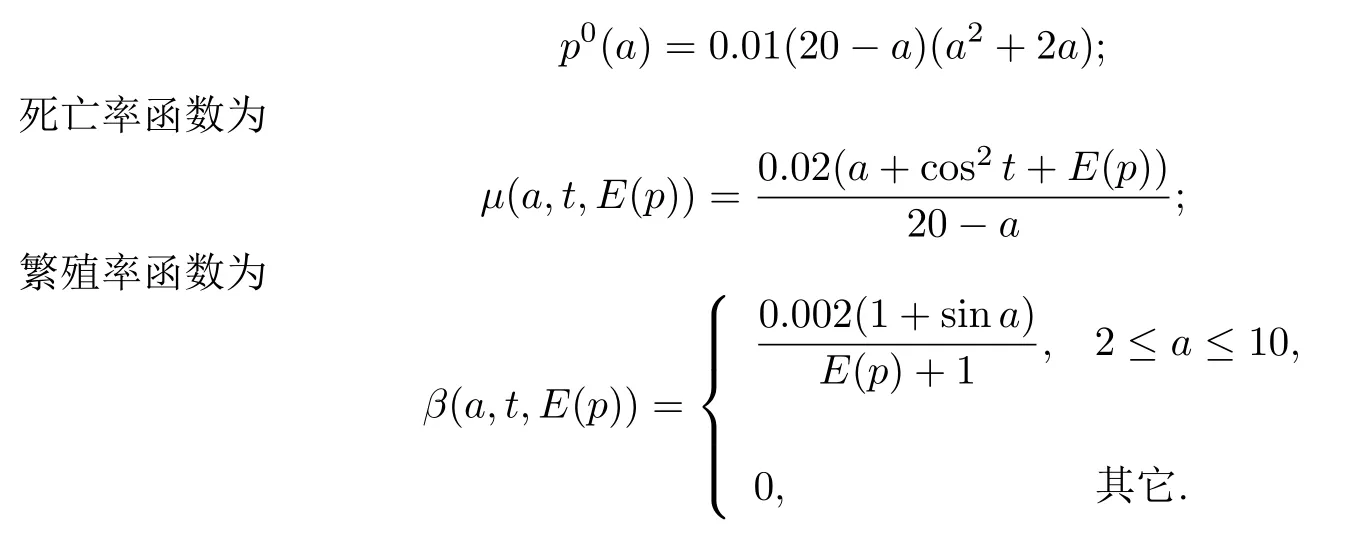
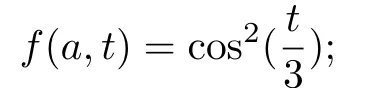
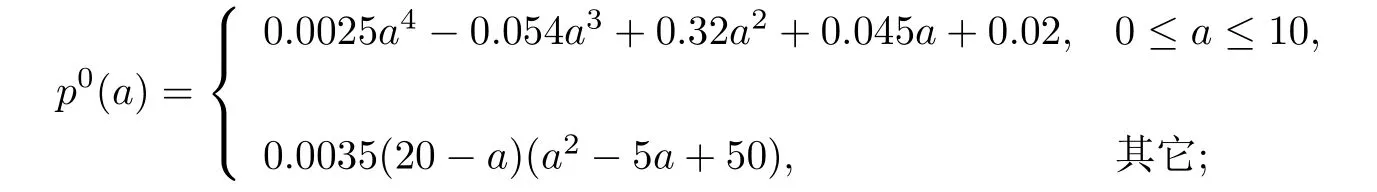
§5 结语

