环Fp×Fp[v]/〈vm −v〉上的线性码及其MacWilliams恒等式
刘家凤,施敏加
(安徽大学 数学科学学院,安徽合肥 230601)
§1 引言
编码理论中最有名的成就之一就是MacWilliams恒等式[1-2],它给出了线性码及其对偶码之间关于汉明重量计数器的关系.Pinheiro在文献[3]中给出了有限域Fq上线性码C的MacWilliams恒等式.近些年,越来越多的编码学者将研究兴趣从有限域转移到有限环上来.如在文献[4]中,施敏加等人给出了Shiromoto在文献[5]中研究的环Zl上关于Lee-重量计数器和Euclidean-重量计数器及其MacWilliams恒等式的反例.文献[6]给出了环Zl上关于Lee-重量计数器和Euclidean-重量计数器及其MacWilliams恒等式存在的充分必要条件.Abdelghany在文献[7]中表明在环Zm上,当m ≥5时关于Lee-重量计数器及其MacWilliams恒等式不存在.在文献[8] 中,zen研究了一个更大的环,有限交换的Frobenius环,研究了该环上关于m-spotty Rosenbloom-Tsfasman重量计数器的恒等式.对于非链环上的线性码及其对偶码之间的各种重量计数器及其MacWilliams恒等式同样也引起了编码学者的兴趣.文献[9]研究了环F2+vF2+v2F2(v3=v)上线性码及其对偶码之间的各种重量计数器及其MacWilliams恒等式.在文献[10]中,施敏加等人在一个特殊的有64个元素的环F2[u,v]/〈u2−1,v3=v,uv=vu〉上研究了线性码的重量计数器及其MacWilliams恒等式.在文献[11]中,研究了ZpZpk-加性码的象的重量计数器并且建立了MacWilliams恒等式.这些结果随后在文献[12]中得以推广.文献[13]研究了非链环F2×(F2+vF2)(v2=v)上线性码及其对偶码的MacWilliams恒等式.
本文将文献[13]中的结果推广到最一般化的情况,假设p是素数.§2研究了阶为pm+1的环Fp ×Fp[v]/〈vm −v〉及环上线性码的结构.为了得到主要的结果,首先需要引入从环Fp ×Fp[v]/〈vm −v〉到的两个Gray映射,并由此给出Lee-重量和Gray-重量的定义.§3研究了该环上线性码的Gray象并基于这两个Gray象分别讨论了这些线性码在两个不同内积的对偶码.§4得到了环Fp×Fp[v]/〈vm −v〉上的三种重量计数器: 完全重量计数器,对称重量计数器和Lee重量计数器以及三种重量计数器之间的关系,同时通过一些例子来验证所得到的结果.
§2 环R上线性码的结构
这一节给出一些基本的定义并研究了环Fp×Fp[v]/〈vm −v〉及环上线性码的特征.

R上的一个线性码C可以定义如下.
定义2.1如果C是Rn的R-子模,则Rn的一个非空子集C被称为长度为n的线性码.
引理2.1在环中,长度为n的线性码C可以被认为是两个长度均为n的线性码C1和C2的直积,即C是C1×C2的等价置换,其中C1在域Fp上,而C2在环Rp上.
例2.1设p=2,m=3.则R=F2×(F2+vF2+v2F2),R2的子集C为

则C是环R的线性码且|C|=32.考虑F2上的线性码C1={(0,0),(0,1),(1,1),(1,0)}以及F2+vF2+v2F2上的线性码C2={(0,0),(0,1),(0,v),(0,1+v),(0,v2),(0,1+v2),(0,v+v2),(0,1+v+v2)},可以发现C置换等价于C1×C2.
§2.1 环R上线性码的Gray映射
本节首先给出从环R到的两个不同的Gray映射,然后基于这两个映射定义了环R上码的Lee-重量和Gray-重量.

若C是R上长为n的线性码,则φ1(C)是长为(m+1)n的线性码,且这一映射可自然扩展到Rn.
命题2.1.1Gray映射φ1是Fp线性的.
例2.1.2考虑例2.1中的线性码C,则

是一个长度为8的二元线性码.
对任意x ∈R,定义x的Lee-重量


命题2.1.6Gray映射φ2是Fp线性的.
例2.1.7考虑例2.1中的线性码C,则

是一个长度为8的二元线性码.
定义2.1.8环R上的Gray-重量wG定义为

例2.1.10考虑例2.1中的线性码C中的码字,x=(1,0)(1,1 +v2)的Lee-重量WL(x)=WL(1,0)+WL(1,1+v2)=3.y=(1,0)(1,1+v+v2) 和z=(0,0)(1,v+v2)之间的Lee-距离dL(y,z)=2.码C的Lee-重量和Lee-距离是相等的,即wL(C)=dL(C)=1.
例2.1.11设C是例2.1中的线性码,则它的最小Gray-重量是2.φ2(C)是长度为8,最小Hamming-重量为2的线性码.
§2.2 环R上线性码的内积
本节基于上述两个不同的Gray映射,在环R上定义了两个不同的内积.

引理2.2.1环Rn上的欧几里得内积是R-线性的.
定义2.2.2设C是R上长度为n的线性码.定义C关于欧几里得内积的对偶码C⊥为

根据欧几里得内积的定义可知,C⊥也是Rn上长度为n的线性码.
例2.2.3考虑例2.1中的线性码C.则


引理2.2.6环Rn中的厄尔米特内积是R-线性的.
定义2.2.7如果C是R上长度为n的线性码,则可以定义C在厄尔米特内积下的对偶码C∗:
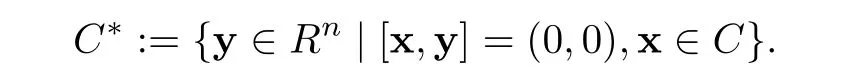
例2.2.8考虑例2.1中的线性码C.有

定理2.2.9若p=2,则Gray映射φ2关于厄尔米特内积是一个保正交性的映射.

下面推论的证明与推论2.2.5相似,所以在这里省略.
推论2.2.10φ2(C∗)=(φ2(C))⊥当且仅当p=2,其中C∗是线性码C的对偶码,且(φ2(C))⊥是φ2(C)的对偶.此外,如果C是一个自对偶码,那么φ2(C)也是一个自对偶码.
§3 MacWilliams恒等式及重量计数器





