双向标量的数学描述与双向标量公式

万学斌

(湖北职业技术学院,湖北孝感 432000)

双向标量的数学描述与双向标量公式

万学斌

(湖北职业技术学院,湖北孝感 432000)

本文重点阐述了双向标量的数学描述,同时说明了双向标量公式在使用中必须注意正方向的匹配问题,一定的公式情形依赖一定的正方向配合,离开了正方向的配合,公式没有任何意义。

双向标量 数学描述 正方向 代数量 双向标量公式

物理学中的标量按数学性质可分为两类:一类是只需用算术量表示的量称为单向标量，如质量、体积、绝对温度和电阻等。这些物理量的特点是没有负的量值，或者说其负的量值没有实际物理意义。这类物理量在数学描述上不会出错，处理起来很简单。

另一类是如电荷量、电流强度、电压、电位、功、势能、摄氏温度等。在物理学理论和实践中经常会遇到这些量，而这些量又是贯穿物理学的始终，处理这些量的时候，往往由于数学描述上的不清晰，物理教材也没有系统的讲解，而是分散在各个不同的部分，或者是直接应用，从而导致处理这些量的时候常常出错，处理好这些量是学习好物理学的关键所在。下面拟就这类物理量有关的问题进行讨论。

1 双向标量

例如电荷量q有电荷量的大小和正负、电流强度有大小和沿着导线两个相反的方向、AB两点的电压有大小和正负、电位也有大小和正负、力对系统做的功有大小和正负、在参考位置确定以后，势能也有大小和正负、在摄氏零度确定后，摄氏温度有大小和正负。

这类物理量有一个共同的特点，就是它们既有大小，又有方向或正负，仅且仅有两个相反的方向或正负，我们把这类物理量称为双向标量。

也就是说，判断一个物理量是否为双向标量，主要是看它是否具有两个彼此相反的方向或者是正负值。按照这样的判断方法，那么时间、高度、一条直线上的分矢量就都可以作为双向标量处理了。因为时间有过去与将来、高度有上与下、一条直线上的分矢量有左和右这两个方向，所以说这些量都可以作为双向标量来处理[1][2]。

在这里不要把双向标量和矢量混淆，双向标量仅且仅有两个两个彼此相反的方向或正负值，而矢量却有无限多个可能方向。

2 双向标量的数学描述

既然物理学中大量的出现双向标量，那么用什么数学工具来描述呢？下面来看看双向标量的两个要素:大小和方向。

首先是看双向标量的大小要素:其实大小是一个相对的量，必须有一个参考点和一个度量单位，如果没有这两项无法确定物理量的大小，例如以长度的度量为例，对于一个一米长的书桌，以书桌的左方为参考点，如果用米作为度量单位度量书桌就是一米长，如果用尺作为度量单位，这个书桌就是三尺长等。当然，在这里我们也可以选择右方为参考点，从右向左度量其长度，也会得出同样的结果。由此可见，双向标量的大小要素可以细分为参考点和度量单位两个要素。对于双向标量的参考点的选择一般是由人为的定义的，其实各类仪表的校零就是一个参考点的校正的问题；对于双向标量的度量单位我们一般选择国际单位或者是行业单位。

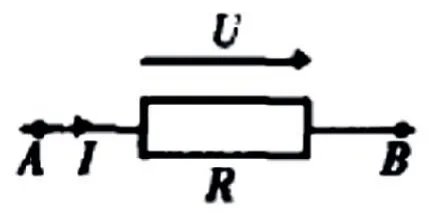
图1 I、U关联方向

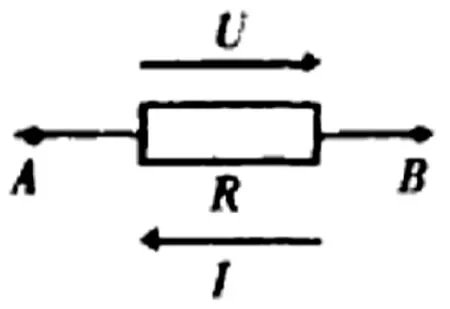
图2 I、U非关联方向

其次是看双向标量的方向要素:由于双向标量具有两个彼此相反的方向或正负，要想确定这两个方向，我们必须规定其中一个方向为正方向，那么，另一个方向就是它的相反方向[1]。

至此为止，我们知道双向标量其实有三个要素，就是参考点、度量单位和正方向。这三个要素都可以是人为规定的，这和数学中的数轴的三个要素是一样的，也就是说，双向标量的几何描述就是数轴，对应的量就是代数量。在今后的物理学学习中一定应该注意双向标量的三个要素，特别是方向要素。这个要素在研究者的心中应该是清清楚楚的，不能有半点的含糊。

3 双向标量公式与正方向匹配

物理学中大部分公式是含有两个或者是多个双向标量的公式。对于这些公式，在使用时一定应该注意物理图像上的正方向匹配问题，下面以我们熟悉的欧姆定律为例说明正方向的匹配问题。

欧姆定律中包含有两个双向标量电流和电压，对于这两个双向标量的正方向规定有两种情形。一种是两个双向标量的正方向规定为一致，如图1所示，我们把这种正方向匹配称为正方向的关联配合，也称为关联方向，在关联方向下，欧姆定律的表示为U=IR。

另一种是两个双向标量的正方向规定为相反，如图2所示，我们把这种正方向匹配称为正方向的非关联配合，也称为非关联方向，在非关联方向下，欧姆定律的公式为U=-IR。

可见，一定形式的公式是依赖正方向配合而存在的，离开了正方向的配合，公式的形式没有任何意义。对于以上欧姆定律的两个公式，它们不仅可以计算I、U的大小，还可以计算I、U的方向。大小就是对应量的绝对值，方向由计算结果的正负数确定，结果为正数，实际方向和正方向一致；结果为负数，实际方向和正方向相反。现在看来，这两个公式的欧姆定律比初中学习的欧姆定律的功能就要强大得多。特别是第一情形下的公式，从表面上看，公式形式一模一样，但是这两个公式却有着不同的内涵，初中的公式只能计算大小，不能计算方向，而这里的公式大小和方向都能够一次计算完成，提高了解决问题的效率[3]。

4 结语

双向标量是有大小和两个彼此相反方向或者是正负数的量，它用代数量表示；在双向标量的公式中一定应该注意各个双向标量的正方向规定，离开了正方向的规定，公式形式没有任何意义[3]。

[1]梁灿彬,秦光戎,梁竹健.电磁学.北京:高教出版社1980.

[2]赵凯华,陈熙谋.电磁学,北京:人民教育出版社,1980.

[3]万学斌.物理学中标量,矢量表示及代数量等式探讨[J].孝感教院学报,1999,(7).

万学斌(1963—),男,湖北孝感人,湖北职业技术学院机电工程学院副教授,主要研究机电一体化、电气基础、电工电子技术应用与安全。