一次一密理论的再认识

陆成刚 ,王庆月

(1.浙江工业大学 理学院,浙江杭州 310023;2.宁夏理工学院计算机学院,宁夏石嘴山 753000)

§1 引言

1882年银行家弗兰克-米勒首次发现使用了一次性密码本[1],通信工程师吉尔伯特-佛纳于1919年被授权了也许是密码史上最重要的一个关于一次一密的专利[2].克劳德-香农在1940年代发现并证明了一次一密方法的理论意义,他的报告于1949年被公开[3].几乎同时期苏联数学家弗拉基米尔-科特尔尼科夫独立地证明了一次一密的绝对安全性[4].王勇提出了密钥分布等概率性与明文概率分布不兼容的问题[5].雷凤宇证明了完善保密性密码体制的条件和存在性[6].本文重新审视了密钥等概率性条件和满足完善保密性的关系,在一个特定的完善保密性角度下推导出明文分布的等概率性.进一步,传统一次一密理论的密钥等概率性条件可以去掉,只保留明文和密钥的互相独立性就能证明完善保密性.这个结果进一步推广了一次一密方法的适用范围,同时指出密钥等概率特性下的一次一密法仍可以适用于信源压缩编码后的明文加密.

§2介绍一次一密法,§3使用概率论证明了它满足完善保密性,并且推导出明文的等概率分布特性.§4使用明文和密钥互相独立作条件证明了完善保密性.

§2 一次一密

考虑有限加法群G,明文,密钥和密文分别是以G作为样本空间的离散随机变量M,K和C,并且在每一个样本点上的概率值都大于零.对明文随机变量M的任一取值m,令任一密钥k(密钥随机变量K的取值)与之运算得到密文c(密文随机变量C的取值),即m+k=c,其中+为G中的加法运算.而解密运算c−k=m,−为加法运算的逆运算.明文和密文之间的运算k=c−m可以解出密钥.一个加密算法,其对应的解密算法和确定密钥的算法决定了三个随机变量M,K和C的三组确定映射

其中f为加密函数,g为解密函数,h可由明文和密文确定密钥,这三个函数是确定的,已知的函数.一次一密的主要实现方式为将加密看作一个过程,则明文序列为与随机变量M同分布的一个随机过程,每次加密参与的密钥视作与K同分布的一个随机过程.在K与M互相独立,并且K的分布为等概率分布(均匀分布)的条件下可以证明一次一密满足完善保密性.

§3 满足完善保密性

见诸于文献的完善保密性主要是指明文与密文互相独立,即

它的密码学含义可以解释为知道密文并不能改善对于明文的认识,即密文没有提供对明文的任何信息.使用信息熵的语言,以密文作条件的明文熵等于明文熵,从而知道明文,密文的互信息为零,即

另外一种常见的完善保密性的定义为

它的密码学意义也很容易理解,就是密文c是由明文密钥对(m1,k1)生成而成还是由(m2,k2)加密而成的可能性没有差异.这个定义等价于联合条件概率分布P((M,K)|C=c)为等概率分布.

定理1以加法有限群G为样本空间的随机变量M,K和C满足f,g和h确定函数组成的式(1),随机变量M,K互相独立,随机变量K概率分布符合均匀分布,则随机变量M,C满足式(2).

证设明文m,密钥k和密文c满足

上面倒数第三个等号利用式(5),倒数第二个等号利用了随机变量K的概率分布符合均匀分布的特性,最后的等号说明密文也符合等概率分布,

以上倒数第二个等号利用了式(5),最后一个等式利用了式(6),这里说明了M,C的互相独立性,即

定理2以加法有限群G为样本空间的随机变量M,K和C满足f,g和h确定函数组成的式(1),随机变量M,K互相独立,随机变量K概率分布符合均匀分布,当变量M,K和C满足式(3)定义的完善保密性时,明文一定符合均匀概率分布.

证由于随机变量M,K互相独立,随机变量K概率分布符合均匀分布,由定理1的证明过程得到式(5),(6)成立,考虑

而式(8)左端是等概率分布的(满足式(3)的完善保密性),于是右端表明明文也是符合等概率分布的.

§4 新条件下满足完善保密性

为保证完善保密性,在定理1中设置了一个先决条件,即密钥的等概率分布特性,实际上这个条件是冗余的,下面通过定理3证明在没有这一条件时一次一密方法能够保证完善保密性.

定理3以加法有限群G为样本空间的随机变量M,K和C满足f,g和h确定函数组成的式(1),随机变量M,K互相独立,则随机变量M,C满足式(2).

证由于式(1)中f,g,h为确定的,已知算法.易知以下三条件熵为零

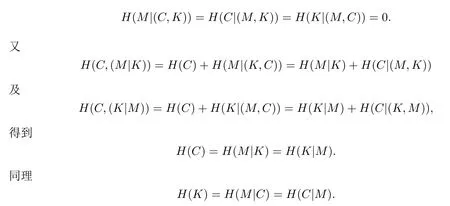
另因随机变量M与K独立,由H(C)=H(M|K)=H(K|M)得到H(C)=H(M)=H(K).所以H(M|C)=H(M),进而满足式(2).此外

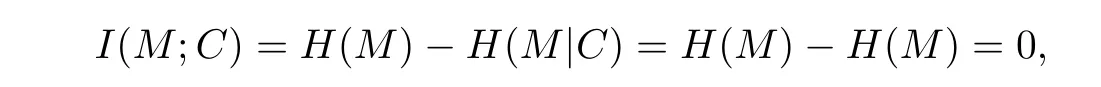
说明明文和密文之间的互信息为零,而这说明明文和密文之间的信道容量为零.

类似在该定理证明中的方法,可得到

这说明在C=c时,联合变量(M,K)的不确定性和M是一个量级的,这也是自然的,因为M确定了,K自然也确定了.假如进一步要求满足式(3)的完善保密性,那么由P((M,K)|C=c)的等概率性,导致H((M,K)|C)取到最大值,即H(M)取到最大,而这实际就是要求明文分布的等概率性.而定理3说明变量M,K互相独立时,就可以满足随机变量M,C互相独立的完善保密性,对明文M的概率分布却没有限制.

此外,定理3说明在一次一密执行时密钥的等概率性实际是不必要的,只要密钥与明文独立无关即可.此外,在满足特定的完善保密性时,密钥等概率特性带来了明文分布的等概率特性的限制,但这并非对适用的明文产生了制约.事实上只要明文经过熵压缩信源编码后的码流均能呈现0,1比特的概率均衡的随机性(如果0,1出现的概率不均衡,说明还有进一步可压缩的空间),这恰恰使得“明文”符合在0,1比特上的等概率特性.因此,在使用密钥等概率特性的一次一密时建议首先对明文进行无损熵压缩编码.

§5 总结与展望

本文重新审视了一次一密的密钥等概率特性与完善保密性的关系,并通过信息熵工具证明了明文和密钥独立无关条件下的一次一密的安全性.将来可以考虑信息熵工具用于对公私钥密码体制的安全性分析的研究.