大学物理中多普勒效应的教学体会

章 敏

(安徽建筑大学 数理系，安徽 合肥 230022)

1 经典多普勒效应

1.1 波源静止，观测者运动

波在介质的速度为u，波源静止，观测者在介质的速度为v观，波相对于观测者的速度为u+v观，观测者接收的频率为

1.2 波源运动，观测者静止

波在介质的速度为u，但由于波源的运动，波长速短了λ-v源T。具体解释如下：当波源静止时，前后相邻两个等相面间的距离为λ，但当波源运动时，前一个等相面自波源出发后，就以速度v源行进，在后一个等相面自波源出发时，波源已向前移动了v源T，这时两个等相面间的距离为λ-v源T，及波长变为λ-v源T。观测者接收的频率为

1.3 波源运动，观测者运动

如果波源和观测者远动方向在同一直线上，结合前两者的结论，观测者接收的频率为

如果波源和观测者远动方向不在同一直线上，那么情况更加复杂。可以将波源和观测者速度沿着某一方向进行分解，波源和观测者速度在这个方向上的夹角分别是α和β，观测者接收的频率为

对该结论进行讨论可得出以下结果：1)v源和v观在连线上运动，α=0，β=0，(1-4)式即化简为(1-3)式，即所说的纵向多普勒效应。而一般情况下v源和v观不变，α，β是随时间变化的，因此，γ'是时间的函数。2)当 u=v源，γ'=γ

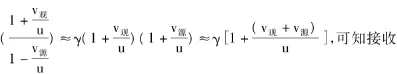
的频率与源与观测者的相对速度有关。

2 相对论多普勒效应

电磁波的速度在相同环境下传播速度是相同的，电磁波的传播速度等于光速，即γλ=c。对不同的参考系测得的波的频率和波长的乘积相同但频率和波长却不同。

我们取相对光源静止的参考系为S系，相对于观察者静止的参考系为S'系，如图。设光源位于S系的O点上，S系相对于S'系以速度v沿x正方向运动。相对于S系，在某一时刻t，光源发出某一相位的等相面，经过时间光源又发出同一相位的等相面，用相对论语言就是：在S系的O点处，发生了两个事件，且时间间隔为如图。

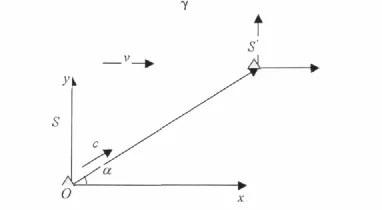
对于S'系：第一个等相面发出的时刻为

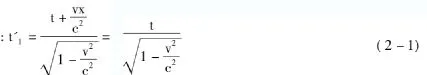
第二个等相面发出的时刻为

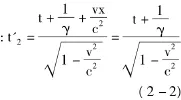
第一个等相面发出的坐标为

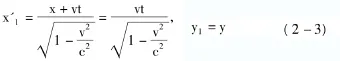
第二个等相面发出的时刻为：

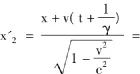
因此，两个等相面的时间间隔为：

则观察者接收的频率为：

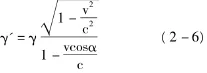
对该结论进行讨论可得出以下结果：1)观测者在相对运动方向上，即即所说的纵向多普勒效应。2)观测者垂直于相对运动方向上，即即所说的横向多普勒效应。3)相对论多普勒效应只与源与观测者相对运动有关。4)当与经典情况下的结论一致，所以经典理论和与相对论理论解释多普勒效应是自洽的。

3 结语

综上所述，运用经典理论和相对论理论，得出多普勒效应的两种不同表达形式。通过分析可得出以下结论：1.经典多普勒效应与源运动和观测者运动都有关，且后两者运动产生多普勒效应的机制也不同;而相对论多普勒效应只与源与观测者相对运动有关。2.在经典多普勒效应中，只考虑纵向多普勒效应;而相对论多普勒效应，不仅有纵向多普勒效应，也有横向多普勒效应。3.两种理论分别适用于多普勒效应的低速源、高速源，在极端情况下，两者的结论是一致的。

[1]程守洙等，普通物理学[M].北京：高等教育出版社，2006.

[2]张三慧等，大学物理学[M].北京：清华大学出版社，1999.

[3]顾建中，普通物理学简明教程[M].北京：人民教育出版社，1977.

[4]杨仲耆，大学物理学[M].北京：高等教育出版社，1981.