具有遗憾值约束的鲁棒性交通网络设计模型研究

刘 慧,杨 超,杨 珺

(华中科技大学管理学院,武汉430074)

具有遗憾值约束的鲁棒性交通网络设计模型研究

刘 慧,杨 超*,杨 珺

(华中科技大学管理学院,武汉430074)

由于交通网络设计决策的长期性,许多参数会随时间而变化,因此在鲁棒性交通网络设计问题中考虑不确定性因素至关重要.当OD需求不确定时,同时考虑期望行程时间和最大遗憾值,引入一种新的鲁棒性度量标准,将α-鲁棒解的概念应用到交通网络设计问题中,提出了一种具有遗憾值约束的鲁棒性交通网络设计模型.然后设计遗传算法求解模型,得出不同遗憾值下网络设计的最佳方案.最后,以Nguyen-Dupius网络作为算例证明了遗传算法求解鲁棒性问题的有效性.详细分析了期望行程时间与最大遗憾值之间的权衡关系,权衡曲线表明,最大遗憾值的降低并不一定导致期望行程时间的较大增加;并将鲁棒优化模型与随机优化模型作比较,结果表明,鲁棒优化模型比随机优化模型更能规避不确定性带来的风险.

系统工程;交通网络设计;遗传算法;鲁棒优化;遗憾值

1 引 言

交通网络设计问题就是在各种给定的约束条件下,选择路段新建(离散)或改善(连续),使其满足某种均衡条件,最优化交通网络的系统性能.许多文献将此问题描述为双层规划或者带均衡约束的数学规划,关于交通网络设计问题的一些模型和算法,可以参考文献[1-5].在实际的交通网络设计中,许多参数(如OD需求、路径的容量和费用等)在网络运行中是不确定的.考虑不确定性对网络设计的影响是投资者应考虑的重要方面.如果为了问题的简化而不考虑这些不确定因素对网络设计的影响,将得到网络设计的次优方案.网络在实际运行中,参数一旦偏离预测值,将会造成运行效率和服务水平低下、资源的浪费等.

由于不确定性对交通网络设计的重要性,近年来逐渐有文献开始考虑其对网络设计的影响. Ukkusuri等[6]研究了基于情景的需求不确定网络设计问题,目标是最小化均值和方差的线性组合,分析不同权重下交通网络设计的最优结构. Ukkusuri等[7]同时考虑需求不确定和需求弹性的多阶段网络设计问题.Chen等[8]研究了需求不确定下交通网络设计的随机多目标模型,提出了期望值、机会约束和概率函数的多目标双层规划模型来规避需求不确定带来的风险.Sharmal等[9]建立了基于需求不确定的多目标网络设计模型,同时最小化均值和方差.Dimitriou和Stathopoulos[10]使用均值模型和机会约束规划模型来研究可靠性随机网络设计问题.Yin等[11]采用“盒子”作为不确定需求的集合,研究了基于随机用户均衡下的连续网络设计问题.Chen等[12]采用条件风险值作为风险指标去优化交通系统的总体性能.Lou等[13]考虑了需求不确定的离散容量扩张,其目标是最小化最大值.Chootinan等[14]提出了新的容量可靠性指标,即路段的交通量小于其容量的概率,并以这个指标来设计随机网络.Karoonsoontawong和Waller[15]考虑短期的交通动态分配和长期的OD需求不确定性,研究了鲁棒性动态连续网络设计模型.Ng和Waller[16]将系统行程时间小于一定值的概率作为约束,研究了均值方差模型.Chen等[17]系统综述了不确定环境下的网络设计问题,并提出了双目标可靠性网络设计模型.孙华等[18]假设OD需求不确定且属于一个有界区间,建立用户均衡约束的交通网络设计的极小极大模型.陆化普等[19]在需求不确定情况下,基于随机双层规划和均值方差理论,建立网络设计的鲁棒优化模型.

以上的研究均表明考虑不确定因素在交通网络设计中至关重要.本文在以上研究的基础上,引入一种新的度量鲁棒性的标准,同时考虑期望行程时间和最大遗憾值两个目标,提出具有遗憾值约束的鲁棒性交通网络设计模型.首先介绍遗憾模型的定义,建立具有遗憾值约束的双层交通网络设计模型,并设计遗传算法求解模型,得出不同遗憾值下,网络设计的最佳方案.最后,利用数值算例说明算法的有效性,分析了期望行程时间与遗憾值之间的权衡关系,并将鲁棒优化模型与随机优化模型进行比较.

2 模型的建立

2.1 遗憾模型

假设Ω是情景的集合.令(Qw)表示情景w下确定性最优化问题.对于每个情景w∈Ω,令表示问题(Qw)的最优目标函数值.假设＞0 (∀w∈Ω).

定义 设α≥0是一个给定的常数.令X是所有问题(Qw)的可行解,zw(X)是问题(Qw)在解X下的目标函数值.X称为α-鲁棒解,若对于所有的w∈Ω有

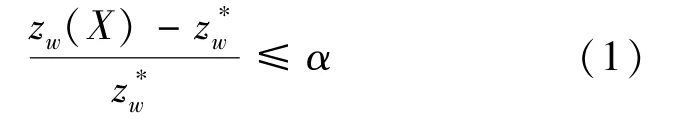
或,等价地

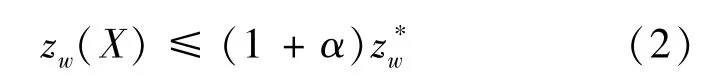
式(1)左端称为情景w下的相对遗憾,绝对遗憾为zw(X)-z*w,下文中提到的遗憾都是指相对遗憾.将α-鲁棒解应用于最小化期望目标函数值则得到如下遗憾模型:

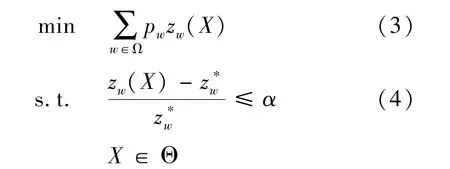
式中 pw表示情景w实现的概率;Θ是对于所有问题(Qw)的可行解集合.

2.2 具有遗憾值约束的鲁棒性交通网络设计模型

在一个交通网络G=(N,A)中,N表示节点的集合,A表示路段的集合.网络中OD需求是不确定的,本文使用情景分析法对OD需求可能出现的情景进行描述,假设情景发生的主观概率可以设定.

在给定的预算下,通过改善已有路段的通行能力,使其在满足用户均衡条件和α-鲁棒解约束下,系统的期望行程时间最优.

为了表述的方便,先将文中用到的参数和变量定义如下:

流量;

pww情景实现的概率;

α最大遗憾值;

ra路段a的现有通行能力;

va对路段a采用扩建策略,路段a增加的通行能力;

γa扩建路段a的成本;

y{1,路段a采用扩张策略,

a

0,路段a维持现状不变.

应用以上符号,本文提出的具有遗憾值约束的鲁棒性交通网络设计问题可以描述为以下双层规划模型:

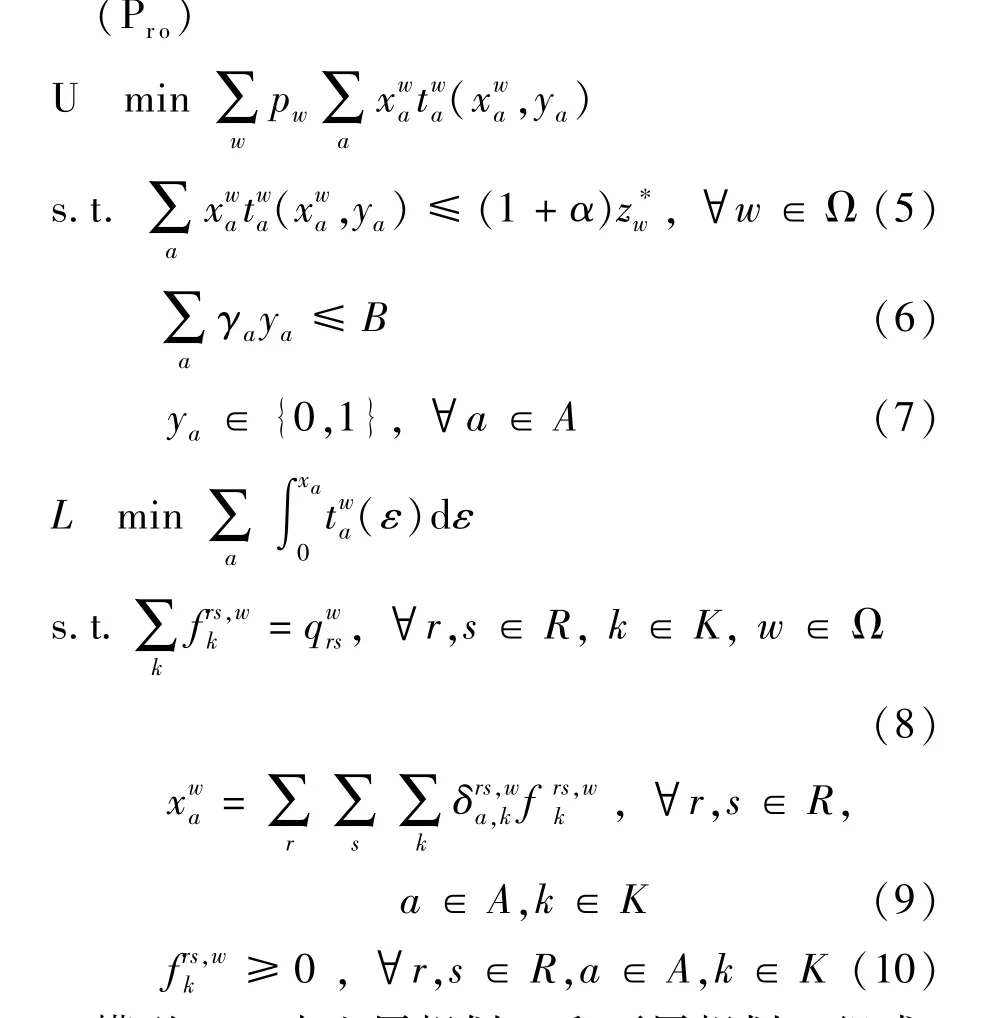
模型(Pro)由上层规划U和下层规划L组成.上下层规划通过决策变量y和路段交通量x相互联系.上层表示系统的目标函数最优,系统的目标函数是行程时间的期望值.约束(5)是鲁棒解约束.约束(6)是预算约束.约束(7)表示y为0-1变量.下层函数是用户均衡问题.路段行程时间用BPR函数表示:.其中FFTa表示路段a上的自由行程时间;Ca表示路段a的容量;σ和β是BPR参数.

模型(Pro)区别于一般的网络设计模型在于:下层L考虑了需求的不确定性;上层U不仅最优化期望的行程时间,还要满足约束(5).约束(5)表明:模型(Pro)的最优解在任何情景实现时的目标函数值与该情景下确定性问题最优目标函数值相对差在给定的范围内.α称为遗憾值,约束(5)称为遗憾值约束.当α=∞时,约束(5)失效,此时的问题为在预算约束下,最小化期望行程时间,即交通网络设计的随机优化模型,记为(Psp),问题(Psp)仅考虑系统行程时间的期望,而不考虑遗憾值.

3 算法设计

3.1 遗传算法

由于模型(Pro)的非线性和非凸性,传统的方法很难用来解具有遗憾值约束的鲁棒性交通网络设计模型.本文使用遗传算法(Genetic Algorithm)来解模型(Pro),主要技术描述如下:

3.1.1 编码与解码规则

本问题只对y进行编码,再将y代入下层规划求解用户均衡问题(UE Assignment),算例中采用Frank-Wolfe来解下层用户均衡问题,Frank-Wolfe算法参考Sheffi(1985)[20].决策变量y为二进制变量,每个变量可表示成1或0,1表示对路段a采用扩建策略,0表示路段a维持现状不变.

3.1.2 计算个体的适应度

个体适应度根据上层规划的目标函数值来计算.问题(Pro)带有约束(5)和(6),本算法利用罚函数法来处理约束条件(5),使用下列改进的适应度:

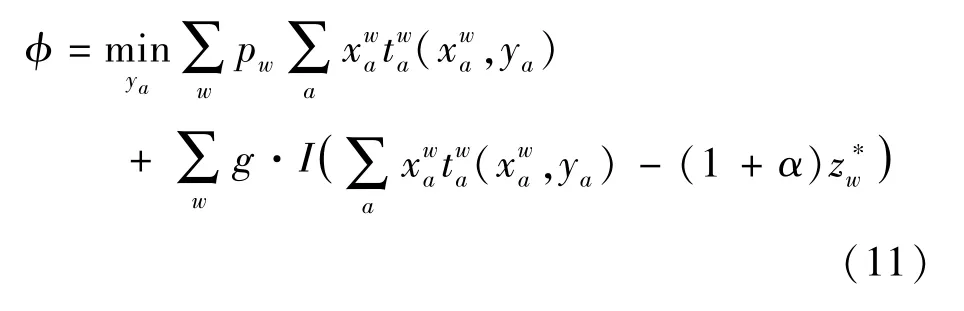
式中 I(x)是示性函数,定义如下:

g是决策者调节的参数,用来惩罚违反遗憾值约束的个体.

对于约束条件(6),本算法使用贪婪法将违背预算约束条件的解转化为可行解.若当前种群中的个体y′不满足预算,即,先求出,然后依次将中最小且y′a=1的路段变为y′a=0,直到满足约束条件(6)为止.该操作在算法中用函数transform()表示,此函数将违背预算约束的解转化为可行解.

3.2 算法步骤

假设最大迭代次数为K.遗传算法求解模型(Pro)具体步骤如下:

Step 1 生成初始种群Y,k←0;

Step 2 根据Y的值,更新网络中的参数;

Step 3 对于每种情景,利用Frank-Wolfe算法求解下层用户均衡问题;

Step 4 将得到的路径流量带入适应度(11);

Step 5 根据个体适应度,对群体进行选择、交叉、变异运算,形成新一代种群Y;

Step 6 用函数transform()将个体对应的解转化为可行解;

Step 7 若k＞K,算法终止;否则k←k+1,转到Step 2.

4 算法的实现与算例分析

4.1 算例的设计

本节的算例中使用Nguyen和Dupius (1984)[21]网络,说明遗传算法求解具有遗憾值约束的鲁棒性交通网络设计模型的有效性.网络结构图如图1所示,Nguyen-Dupius网络被广泛用于交通均衡问题的研究中.对鲁棒性交通设计问题用MATLAB对第3节提出的算法进行编码,然后在CPU为Intel Core i5-2450M 2.50GHz,内存为4.00GB的计算机上进行试验.Nguyen-Dupius网络的参数见表1.表2为OD需求的均值,所有OD对之间独立.假设需求的变异系数取0.5,群体的大小取pop_size=25.采用无回放余数随机选择,交叉概率取在0.7-0.95之间,变异概率取在0.01-0.2之间.最大循环次数为500,违背鲁棒性约束的惩罚因子g=50.假设若对路段a采用扩建策略,则路段a通行能力增加100%,则扩建后路段a通行能力Ca=(1+ya)ra.算例中相对遗憾值取0.65.

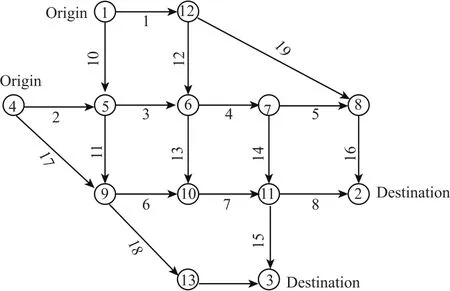
图1 Nguyen-Dupius网络Fig.1 Nguyen-Dupius test network

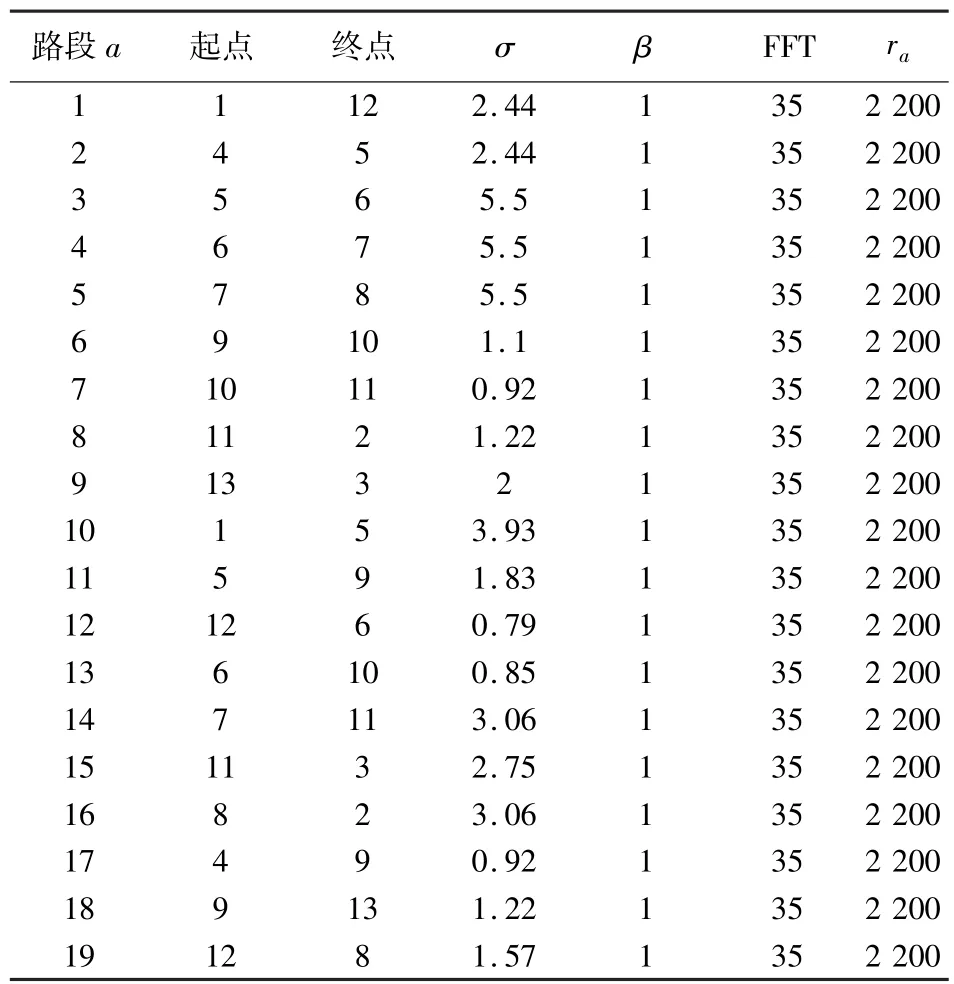
表1 Nguyen-Dupius网络参数Table 1 Network parameters for the Nguyen-Dupius network

表2 Nguyen-Dupius网络的期望OD需求对Table 2 The expected OD demand for the Nguyen-Dupius network

4.2 遗传算法性能测试

用第3节提出的算法对鲁棒优化模型(Pro)进行求解,遗传算法的进化过程如图2所示,当进化进行到大约200次时,用遗传算法求得的解逐渐收敛到最优解.为了测试不同参数对遗传算法结果的影响,本节还对OD需求变异系数分别取0.3和0.6的情况,随机生成OD需求,进行测试.算例均表明,遗传算法在进化到200次左右,遗传算法的解逐渐收敛到最优解.

4.3 数值结果与分析

根据4.1节设计的算例,OD需求的变异系数取0.5,随机生成需求量,利用本文第3节设计的遗传算法,在不同遗憾值下求得的最优解和最优值如表3所示,表3最后一行表示模型(Pro)的目标函数值,即总的系统行程时间(TSTT,total system travel time).从表3可以看出,随着遗憾值的增加,期望行程时间降低.

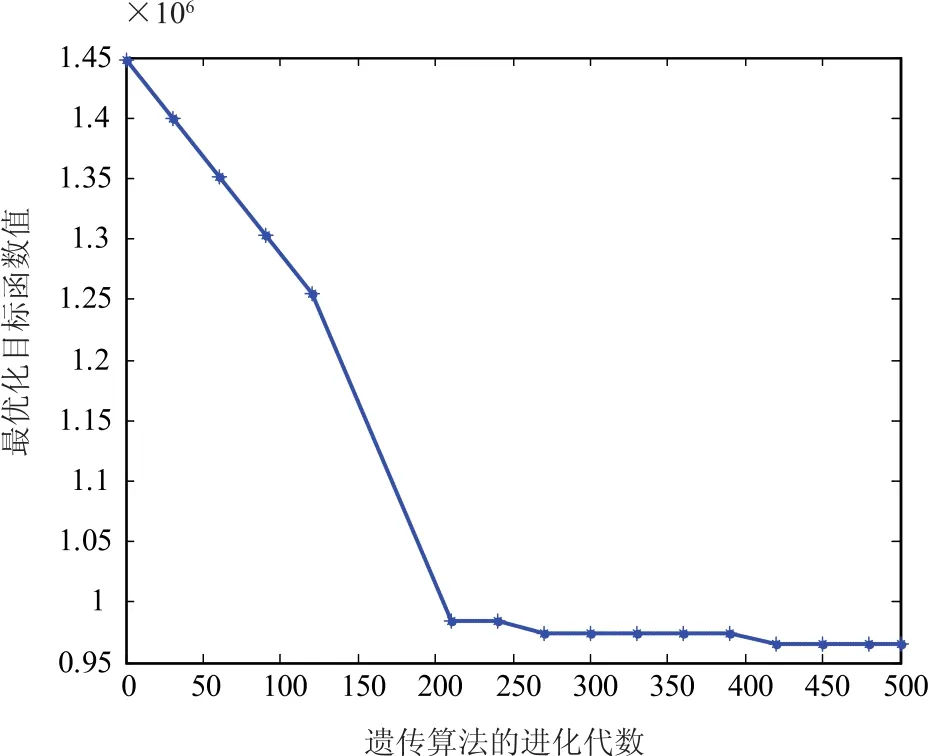
图2 Nguyen-Dupius网络设计种群进化过程Fig.2 Population evolution process for designing Nguyen-Dupius network

具有遗憾值约束的鲁棒性交通网络设计模型的一个重要目的是降低最大遗憾值(通过选择不同的α)的同时尽可能减少期望行程时间的增加,即期望行程时间与最大遗憾值之间的权衡.为了阐述这种权衡关系,本节通过调节α的值来生成期望行程时间与最大遗憾值的权衡曲线.首先,令α=∞,求解模型(Pro),即求解随机交通网络设计模型(Psp),记录最优值和最大遗憾值,见表4中第二行.然后,逐渐降低α的值,求解模型(Pro),直到可行解集为空集为止.不同遗憾值下的目标函数值和最大遗憾值如表4所示.第一列表示用来求解模型(Pro)的不同遗憾值;第二列表示利用遗传算法求得的目标函数值;第三列表示目标函数值相对于α=∞时增加的百分比;第四列表示各种情景下的最大遗憾值;第五列表示最大遗憾值相对于α=∞时降低的百分比.期望行程时间与最大遗憾值的权衡曲线如图3所示.

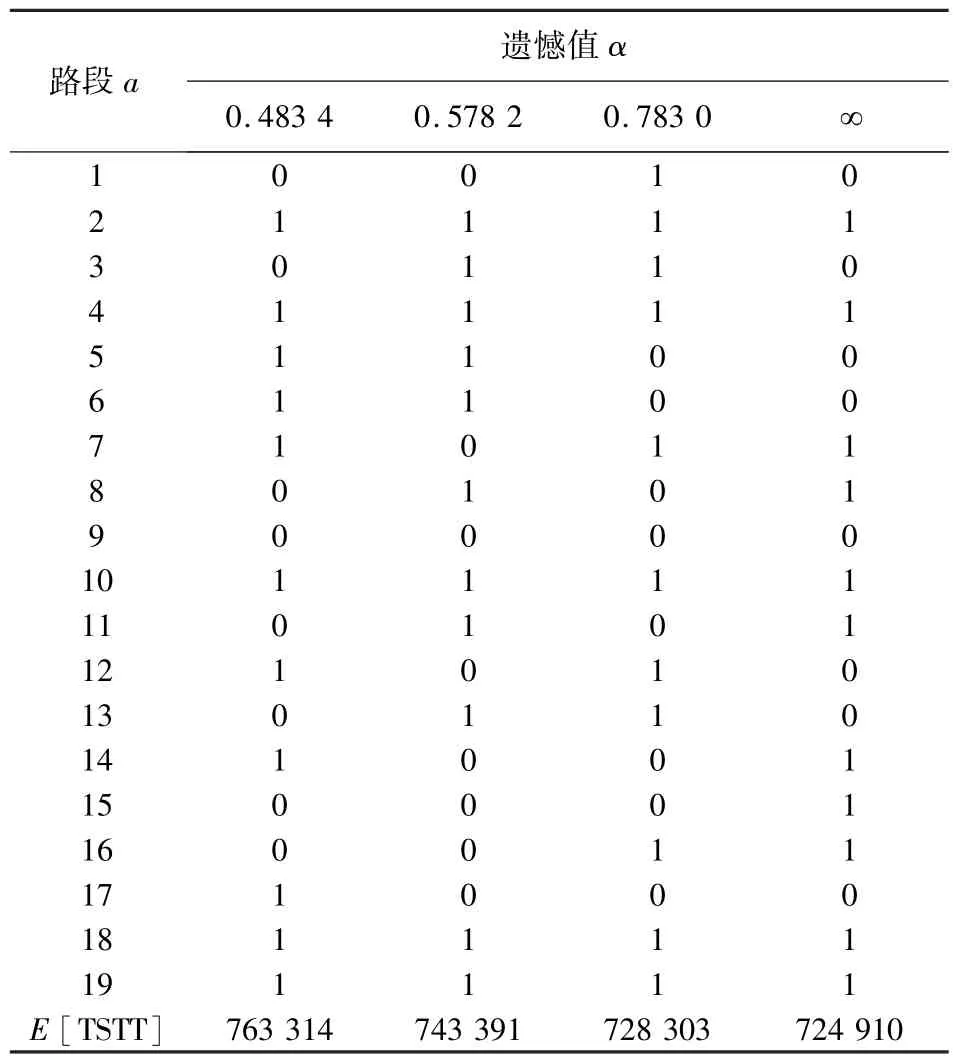
表3 不同遗憾值下鲁棒优化模型的最优解Table 3 The optimal solution of robust network design model for different value of α

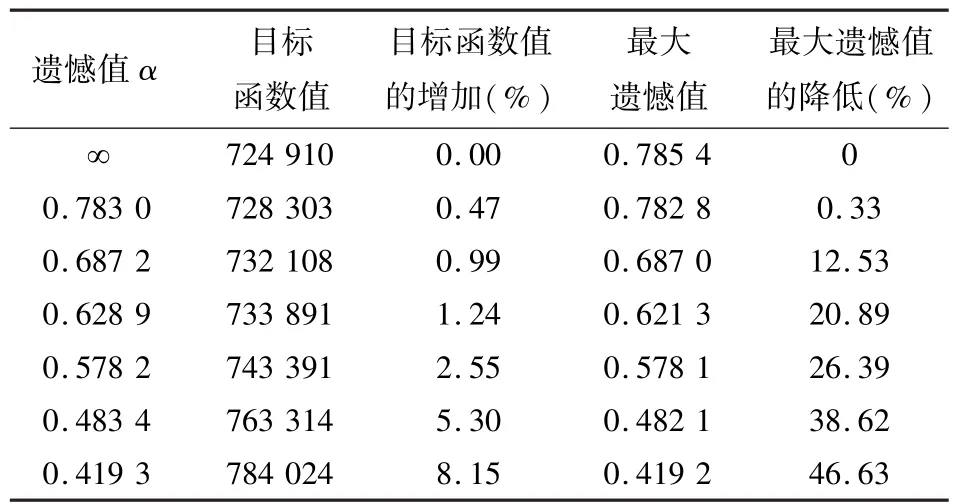
表4 不同遗憾值下的目标函数值与最大遗憾值Table 4 The optimal objective value and the maximum regret value for different value of α

显然,最大遗憾值的较快降低并不一定以目标函数值的较大增加为代价.例如,当α=0.578 2时,最大遗憾值降低26.39%,而目标函数值仅增加2.55%,这说明较强的鲁棒性不一定意味着期望行程时间的较大增加.从图3也可以清楚地看到这一点,图3中的权衡曲线比较陡峭,尤其是最大遗憾值较大时,说明较少的增加期望行程时间可能换来遗憾值的较大降低.根据期望行程时间与最大遗憾值之间的权衡关系,交通网络的设计者可以根据期望行程时间,计算出最大遗憾值;或者根据最大遗憾值的限制,计算出期望行程时间.

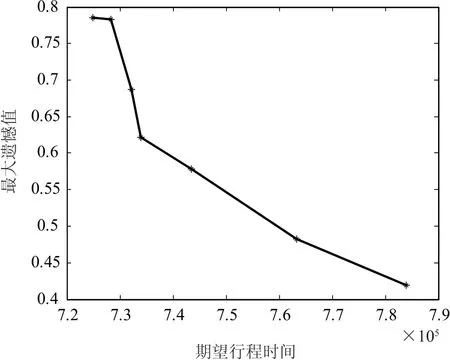
图3 期望行程时间与最大遗憾值的权衡曲线Fig.3 Trade-off curve of objective value and the maximum regret value

4.4 鲁棒优化模型与随机优化模型的比较

本节将带有遗憾值约束的鲁棒优化模型(Pro)与随机优化模型(Psp)的结果进行比较.针对上述设计的交通网络,分别用鲁棒优化模型(Pro)和随机优化模型(Psp)对交通网络设计问题进行求解,在两个模型参数保持一致的情况下,比较两者的性能.

令w情景下确定性模型(Pw)最优目标函数值为,鲁棒优化的解对在情景w下的目标函数值为,随机优化的解在情景w下的目标函数值为.取与的相对遗憾值100%,与的相对遗憾值100%.数值计算结果如表5所示.随机优化模型的最优解在各种情景下目标函数的平均值为924 604,鲁棒优化模型的最优解在各种情景下目标函数的平均值为965 167.显然,随机优化模型的平均值小于鲁棒优化模型的平均值,后者与前者的相对差值为4.38%.但是,这只是目标函数值的差异,而二者同确定性问题最优值的差异,即和,也不容忽视.从表5可以看出,随机优化的解在10种情景下,最大遗憾值为54.70%,最小遗憾值为1.03%,而鲁棒优化的解在10种情景下,最大遗憾值为39.64%,最小遗憾值为21.75%.前者遗憾值的方差为2.97%,而后者遗憾值的方差仅为0.27%.表明前者遗憾值的波动较大,而后者较小.鲁棒优化模型的最优值虽然比随机优化的最优值增加了4.38%,但是前者遗憾值的波动比后者降低了90.94%.

本节随机生成的其他算例也表明,鲁棒优化模型的设计结果虽然比随机优化模型期望值大,但是前者遗憾值的波动较小.即鲁棒优化与随机优化相比,目标函数值的增加较小,但是却能使最大遗憾值和遗憾值的波动都有较大的降低.人们对交通网络设计决策的评价往往是不确定性情景实现后(可以观测到具体的参数值)做出的,利用鲁棒优化模型,使人们对交通网络系统决策方案评价的波动更小.网络系统对各种情景表现出不敏感性,使得网络设计的鲁棒性更强.因此,鲁棒优化模型设计出的交通网络能够较好地规避不确定性带来的风险.

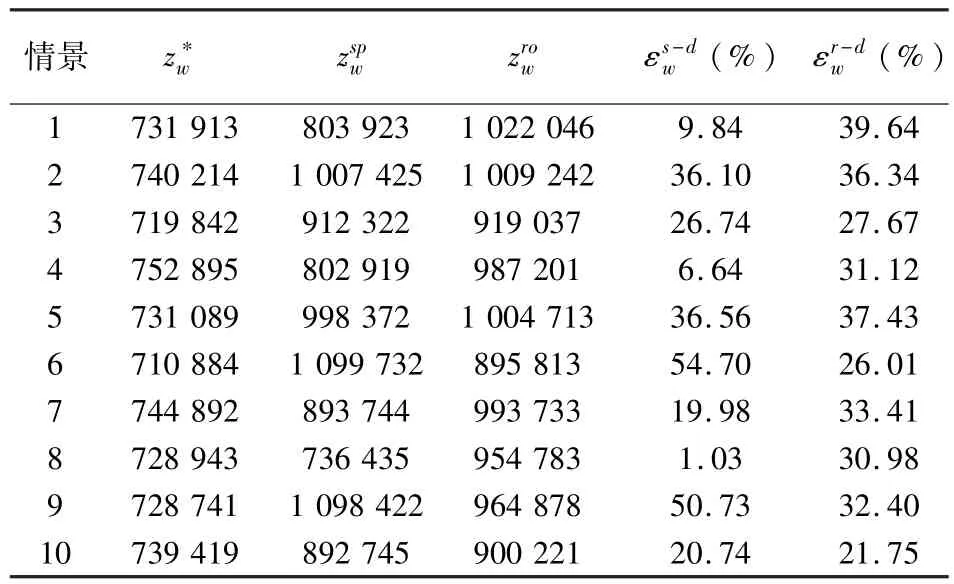
表5 鲁棒优化与随机优化的结果比较Table 5 Comparison between the results of robust optimization and the stochastic optimization

5 研究结论

许多不确定因素影响着交通网络的设计,明确考虑这些不确定因素对网络设计方案的影响至关重要.研究不确定性问题的方法主要有随机优化和鲁棒性优化两种.本文结合随机优化和鲁棒性优化的优点,在假设OD需求不确定的情况下,引入一种新的度量鲁棒性的标准,即α-鲁棒性,提出具有遗憾值约束的鲁棒优化模型,即在后悔值带有约束的情况下,最小化期望系统行程时间.数值算例说明了最大遗憾值的较快降低并不一定以目标函数值的较大增加为代价,即较强的鲁棒性不一定意味着期望行程时间的较大增加.与随机优化模型相比,鲁棒优化模型设计出的交通网络能够更好地规避不确定性带来的风险.本文提出的具有遗憾值约束的交通网络设计模型为决策者提供了一种新的鲁棒性标准,使交通网络的性能在参数摄动的情况下鲁棒性更强.然而,本文的算法用于中等规模的网络和数量较小的情景时比较有效,对于大规模的网络和大量的情景,计算时间显著增加,设计有效的算法是以后深入研究的问题.采用系统总走行时间的总阻抗的期望是不确定模型中最常用的目标,处理不确定问题的模型还有机会约束模型、概率模型、α可靠性模型等,如何将α-鲁棒解与这些模型结合起来,也是今后我们要研究的一个重要问题.

[1] Unnikrishnan A,Lin D Y.User equilibrium with recourse:continuous network design problem[J]. Computer-Aided Civil and Infrastructure Engineering, 2012,27(7):512-524.

[2] Chiou S.Bilevel programming for the continuous transport network design problem[J].Transportation Research,2005,39(4):362-383.

[3] Davis G A.Exact local solution of the continuous network design problem via stochastic user equilibrium assignment[J].Transportation Research,1994,28 (1):61-75.

[4] Farvaresh H,Sepehri M.A single-level mixed integer linear formulation for a bi-level discrete network design problem[J].Transportation Research Part E: Logistics and Transportation Review,2011,47(5): 623-640.

[5] Xu T Z,Wei H,Hu G H.Study on continuous network design problem using simulated annealing and genetic algorithm[J].Expert Systems with Applications, 2009,36(2):1322-1328.

[6] Ukkusuri S V,Mathew T V,Waller S T.Robust transportationnetworkdesignunderdemand uncertainty[J].Computer-AidedCiviland Infrastructure Engineering,2007,22(1):6-18.

[7] Ukkusuri S V,Patil P.Multi-period transportation networkdesignunderdemanduncertainty[J]. TransportationResearchPartB:Methodological, 2009,43(6):625-642.

[8] Chen A,Kim J Y,Lee S,et al.Stochastic multiobjective models for network design problem[J]. Expert Systems with Applications,2010,37(2): 1608-1619.

[9] Sharmal S,Ukkusuri S V,Mathew T V.Pareto optimalmulti-objectiveoptimizationforrobust transportationnetworkdesignproblem[J]. TransportationResearchRecord:Journalofthe Transportation Research Board,2009,2090:95-104. [10] Dimitriou L,Stathopoulos A.Reliable stochastic design of road network systems[J].International Journal of Industrial and Systems Engineering,2008,3(5): 549-574.

[11] Yin Y,Madanat S M,Lu X.Robust improvement schemes for road networks under demand uncertainty [J].European Journal of Operation Research,2009, 198(2):470-479.

[12] Chen A,Kim J,Zhou Z,et al.Alpha reliable network design problem[J].Transportation Research Record, 2007,2029:49-57.

[13] Lou Y,Yin Y,Lawphongpanich S.A robust approach to discrete network designs with demand uncertainty [J].Transportation Research Record,2009,2090: 86-94.

[14] Chootinan P,Wong S C,Chen A.A reliability-based network design problem[J].Journal of Advanced Transportation,2005,39(3):247-270.

[15] Karoonsoontawong A,Waller S T.Robust dynamic continuousnetworkdesignproblem[J]. Transportation Research Record,2007,2029:58-71. [16] Ng M,Waller S T.Reliable system-optimal network design:convex mean-variance model with implicit chance constraints[J].TransportationResearch Record,2009,2090:68-74.

[17] Chen A,Zhou Z,Chootinan P,et al.Transport network design problem under uncertainty:a review and new developments[J].Transport Reviews:A Transnational Transdisciplinary Journal,2011,31 (6):743-768.

[18] 孙华,高自友,龙建成.不确定OD需求下连续交通网络设计的鲁棒优化模型[J].交通运输系统工程与信息,2011,11(2):70-76.[SUN H,GAO Z Y, LONGJC.Therobustmodelofcontinuous transportation network design problem with demand uncertainty[J].Journal of Transportation System Engineering and Information Technology,2011,11 (2):70-76.]

[19] 陆化普,蔚欣欣,卞长志.OD需求不确定的离散交通网络设计模型研究[J].公路交通科技,2011, 28(5):128-132.[LU H P,WEI X X,BIAN C Z. Modelandalgorithmofdiscretenetworkdesign problem under OD dem and uncertainty[J].Journal ofHighwayandTransportationResearchand Development,2011,28(5):128-132.]

[20] Sheffi Y.Urban transportation networks:equilibrium analysiswithmathematicalprogrammingmethods [M].Prentice-Hall,Englewood Cliffs,NJ,1985.

[21] Nguyen S,Dupius C.An efficient method for computing trafficequilibriainnetworkswithasymmetric transportation costs[J].Transportation Science, 1984,18(2):185-202.

Robust Transportation Network Design Modeling with Regret Value

LIU Hui,YANG Chao,YANG Jun
(School of Management,Huazhong University of Science&Technology,Wuhan 430074,China)

Based on long-term transportation network design decisions and potential parameter variations,it is important that demand uncertainty is considered in transportation modeling.In this paper,we present a novel robustness measure that combines the two objectives by minimizing the expected travel time while bounding the relative regret in each scenario facing uncertain origin-destination demand(OD demand).The concept of α-robust solution is introduced into the transportation network design problem.We propose a robust transportation network design model with regret value constraints,then design an algorithm based on the genetic algorithm to solve the problem and obtain the optimal solutions for different regret values. Finally,numerical results based on the Nguyen-Dupuis network validate the effectiveness of the algorithm. While detailed analysis on trade-offs,between the expected travel time and the maximum regret value,shows that large reductions in maximum regret do not necessarily result in a great increase in expected travel time. Meanwhile,we compared the robust model presented with the stochastic model and numerical examples demonstrate that the robust planning network is more reliable and less risky than the stochastic model if demand uncertainty is considered in modeling.

system engineering;traffic network design;genetic algorithm;robust optimization; regret value

U491

: A

U491

A

1009-6744(2013)05-0086-07

2012-10-17

2013-01-29录用日期:2013-02-22

国家自然科学基金资助项目(70871044,71172093);教育部人文社会科学研究青年基金项目(10YJC630331).

刘慧(1982-),女,湖北谷城人,博士生.

*通讯作者:chao_yang@mail.hust.edu.cn