基于离站时刻协调的地铁换乘站列车衔接优化研究

白广争,郭 进*,石红国,杨 扬,张太花

(西南交通大学a.信息科学与技术学院;b.交通运输与物流学院,成都610031)

基于离站时刻协调的地铁换乘站列车衔接优化研究

白广争a,郭 进*a,石红国b,杨 扬a,张太花a

(西南交通大学a.信息科学与技术学院;b.交通运输与物流学院,成都610031)

通过协调城市轨道交通网络中换乘站各方向列车的离站时刻,实现减小旅客的换乘等待时间.分析了多条线路以不同形式相交情况下换乘站列车的到发接续关系,得出换乘接续方向总数的计算公式.在此基础上,以协调时段内各个换乘接续方向上所有换乘旅客总等待时间最少为目标建立了模型.结合丢弃法,设计针对模型的简单遗传算法(SGA).最后,以两线路相交为例做模型验证,并根据设计的算法求解,得出部分优化解.计算结果表明,文中模型能有效减少旅客换乘等待时间.本研究可为网络化运行条件下列车开行方案的制定及优化调整提供支持.

城市交通;换乘衔接优化;简单遗传算法;换乘站;协调模型

1 引 言

换乘站是旅客在相交线路间进行换乘的场所,是轨道交通网络中的节点,决定着网络客流的流畅度.另外,旅客在换乘站滞留时间的长短直接影响旅客出行时间及企业提供的服务水平.因此,提高换乘效率,对城市轨道交通网络化运营发展有重要意义.然而,当换乘站建成以后,换乘站站台大小、换乘通道数及换乘方式等都已基本确定,这些因素决定了车站的最大换乘能力,在此基础上,只有合理进行行车组织,加强线路间的运营协调性,才能达到提高换乘效率的目的.

为了使线路输送到换乘站的换乘客流快速被接续线列车运走,以减小旅客的换乘等待时间,需要对各线路上下行方向列车的离站时刻进行协调,使换乘接续方向上列车能够达到良好的接续关系[1-5].但是,由于换乘站存在多种换乘接续关系[6],其客流输送线同时承担着客流接续线的角色,且要考虑客流的到达分布等因素,因而,要使得各个方向的换乘客流接续同时达到最优很难实现.只有根据“按流开车”的行车组织理念,结合客流的实际特征,通过协调,使所有乘客的换乘等待时间总和最小,这样才能达到优化的目的.

本文首先分析了一个换乘站中所有存在的换乘接续方向数的计算方法,然后对单个换乘站各方向列车的发车时刻进行协调,再以站内换乘乘客总候车时间最小为目标建立模型,最后设计简单遗传算法,并做实例验证.

2 换乘站换乘接续计算

乘客在换乘站从一条线路的某个方向,换乘到另一条线路的某个方向,这就形成了一个接续方向.设存在n条线路在换乘站相交,同一线路的上、下行之间不形成换乘关系,则换乘站共存在的换乘接续方向数分两种情况计算.

(1)换乘站为n条线路的中间站.

每条线路分为上行和下行两个方向,每条线路需要和另外(n-1)条线路的上下行产生双向的换乘关系,由此,可通过式(1)描述换乘站共产生的换乘接续方向数f1.

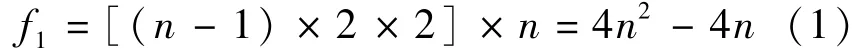
(2)换乘站为n1条线路的中间站,为(n-n1)条线路的终端站.

当换乘站作为一条线路的终端站时,该线路缺少了某一方向的客流输送能力和另一方向的客流接收能力,造成接续关系减少2×[2×(n-1)]个,而这样的线路存在n1条.由此,得出换乘站共存在换乘接续方向数f2如式(2).

3 换乘站列车离站时刻协调模型

列车在相交线路中各自采取均衡行车的方法运行,形成稳定的“衔接周期”[2],即当衔接方向上的两条线路的列车行车间隔固定时,分别为h1和h2,则该两条线路以lcm(h1,h2)为周期形成衔接关系.文献[2]即以“衔接周期”内旅客总换乘候车时间最短为目标.但是,在实际运营过程中,每趟列车带来的换乘旅客量各不相同,旅客在每个“衔接周期”内的到站量分布并不一定相同,因此,在一个“衔接周期”内换乘旅客总等待时间最少并不能代表在其他“衔接周期”内的换乘旅客总等待时间也最少.鉴于此,为了保证模型的普适性,本文以整个协调时段内所有旅客的换乘总等待时间最少为优化目标建立模型.

3.1 条件假设

设所协调时段为[ta,tb],为了降低问题复杂度,对运行条件作如下假设:

(1)线路上、下行列车独立运行,各自到达及离开换乘站的时刻相互没有制约关系.

(2)旅客均能乘上所遇到的第一趟换乘列车,不会因为拥挤而错过,即运能是充足的.

(3)协调时段内,同一线路的同一方向上列车等间隔运行.

(4)同一线路的上、下行之间不产生换乘关系.

3.2 符号说明

为了方便问题描述,对运行过程中的参数作如下符号说明.

n——经过换乘站的线路数.

Rij——线路i的j方向,j=1,2.其中j=1表示上行;j=2表示下行;i=1,2,…,n.

Lij——[ta,tb]内Rij上各列车驶离换乘站的时刻集合.

Dij——[ta,tb]内Rij上各列车在换乘站的停站时间集合.

Aij——[ta,tb]内Rij上各列车到达换乘站的时刻集合.

hij——[ta,tb]内Rij上各列车的行车间隔.

M——[ta,tb]内换乘站所有接续关系集合.即M={Rij→Rpq｜i≠p;i,p∈{1,2,…,n};j,q∈{1,2}}.

3.3 离站时刻协调模型

模型建立过程中,首先确定与换乘站相关的列车运行基本参数,包括到站时刻及离站时刻的表示及相关约束;然后计算一种换乘接续关系下所有旅客的换乘等待时间;最后得出换乘站中所有换乘旅客的等待时间表达式,并以此值最小作为模型的目标.

3.3.1 换乘站列车到发关系分析

在所协调时段[ta,tb]内,由于列车的行车间隔hij保持不变,因此,对于线路i的j方向上各列车在换乘站的离站时刻可以根据时段内第一趟列车的离站时刻确定,如式(3)所示:

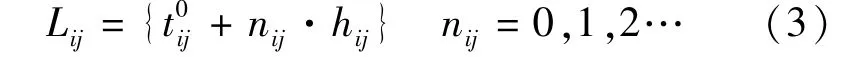
式(3)中nij满足如下约束:根据式(3)知,决定了协调时段内线路i的j方向上后续列车的离站时刻.列车发车的周期性使得对于的取值只需探讨在一个行车间隔[ta,ta+hij)内的分布即可,即满足式(5)约束.

根据线路i的j方向列车的离站时刻集合Lij和列车停站时间集合Dij,可以确定列车的到站时刻集合Aij,如式(6)所示:

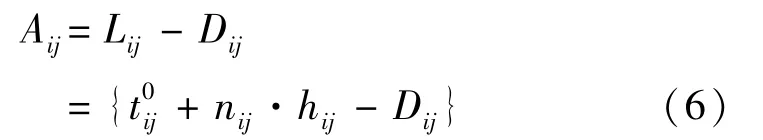
在平行运行图中,停站时间Dij根据高峰小时客流量大小计算设定.通过以上分析可知,各基本运行参数均可以由协调时段内各方向第1趟列车离开换乘站的时刻表示,因此,换乘站列车的换乘协调可转化为针对时段内各方向第1趟列车的离站时刻协调. 3.3.2 换乘接续关系分析

以协调时段内旅客由线路i的j方向第y趟列车向线路p的q方向第x趟列车换乘为研究对象.该接续方向能否衔接成功由与决定.要建立这种换乘接续关系,旅客由线路i的j方向第y趟列车下车,走行至线路p的q方向站台的时刻(+应不晚于线路p的q方向第x趟列车的离站时刻,且晚于第x-1趟列车的离站时刻,如式(7)所示.根据线路中行车间隔约束,得出式(8).

式(9)求得一名旅客产生的换乘候车时间.该对列车y→x共产生名换乘旅客,且在该接续方向上,协调时段内有多趟输送车和接续车形成接续关系,由此,可以求得在协调时段内该接续方向上所有换乘乘客产生的候车时间,如式(10)所示:

3.3.3 换乘站总候车时间计算

以上讨论了在协调时段内一个换乘接续方向上所有换乘旅客候车时间的计算方法.根据第1节的分析,一个换乘站通常存在多个换乘接续方向.为了使换乘站换乘协调总体得到优化,需要对换乘站内所有接续方向旅客总候车时间进行计算,如式(11)所示:

换乘站列车到站时刻的协调目标即为使本站所有换乘旅客等待时间最小.由此,得出模型的目标函数F如式(12)所示:

根据以上分析,式(3)～式(12)共同构成换乘站列车离站时刻协调优化模型,其中式(12)为模型的目标函数,其余各式分别描述了各参数之间的关系及相关约束.

4 算法设计

由于模型中可行解空间非常大,涉及参数较多,如果对解空间进行枚举,寻找最优解的效率较低,因此,设计算法进行模型求解是必要的.

在优化求解算法中,遗传算法理论和方法较为完善,以模式定理为支撑的简单遗传算法(SGA)在应用领域取得了比较好的效果,本模型采用SGA求解,算法具体设计过程如下.

4.1 编码

采用二进制编码方式,编码对象为协调时段内各方向初始列车在换乘站的离站时刻.编码的总长度L由的取值范围及经过换乘站的线路数量确定,其中取值范围参见模型中式(5)约束.

4.2 生成初始种群

利用计算机随机产生规模为M的初始种群.为了提高初始种群的质量,对随机产生的个体进行筛选,避免不符合约束条件的个体进入初始种群中.M的取值通常根据模型解空间的大小确定.当解空间较大时,M的取值也相应较大;反之,M的取值较小.一般M取值范围为200～1 000.

4.3 确定适应度函数

适应度函数用于判断个体优劣的程度,为非负数.一般适应度函数值与个体优劣呈正相关关系,考虑文中模型目标函数为求最小值,因此可以以目标函数的倒数作为适应度函数f,如式(13),式中F为目标函数式(12).

另外,对于不满足模型中约束条件的个体,将其适应度值设置为0,阻止其进入下一代.

4.4 遗传算子设置

遗传算子主要包括选择、交叉和变异三方面.选择操作是实现种群进化过程中优胜劣汰的重要机制,设计选择算子为轮盘赌法,为了提高进化速度及稳定性,在选择时,采取精英保留策略.即,将前一代的最优个体保存到下一代,替代后代中的最差个体,且不参与交叉和变异.交叉分为单点交叉、多点交叉和均匀交叉,本算法采用单点交叉的方法.变异分为局部变异和全局变异两种,本算法采用全局变异的方法,即种群的每个个体随机选择一个位置进行变异.交叉概率Pc和变异概率Pm通常根据实际案例确定.一般Pc建议的取值范围是0.4～0.99,Pm取值范围为0.0001～0.5[7].在实际操作中采取分别对Pc和Pm取不同的值组合,根据适应度值变化规律确定参数的合理值.

4.5 算法终止

算法在迭代若干次后终止,终止条件一般设置为:进化代数限制、计算耗费时间限制等.本算法设置终止条件为确定的进化代数P.即当进化达到代数P时,算法自动终止.P通常设置为100～1 000.

5 案例分析

如图1所示,线路L1与线路L2相交于换乘站St1.分别以平峰时段10:00～12:00和早高峰时段7:00～9:00为例验证模型.

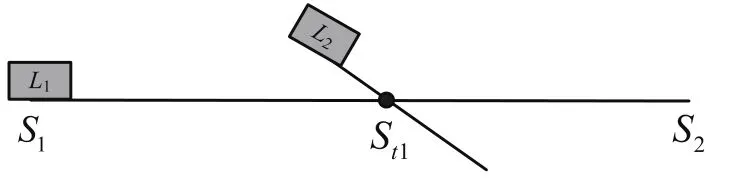
图1 两线相交换乘站示意图Fig.1 Two lines intersection diagram

5.1 平峰时段案例

5.1.1 初始数据准备

取协调时段10:00～12:00,为了计算方便,将协调时段的起始时刻10:00作为0时刻.协调时段内各线路行车间隔h11=300 s,h12=270 s,h21=330s,h22=300 s.线路间纯换乘时间均为100 s.停站时间D11=D12=40 s,D21=D22=35 s.假设各线路各方向每趟列车带来的换乘客流由协调时段内该线路该方向总换乘客流除以开行的列车对数计算得出,如表1所示.表1中“L1上”表示线路1上行,“L1下”表示线路1下行,其他同理.单元格中数据表示所在行方向的一列车所带来的要换乘到所在列方向的客流量.

根据算例中h11、h12、h21、h22的取值均不超过29=512 s,因此,每个初始离站时刻可以采用9位二进制编码,共4个列车运行方向,则L=36.种群规模N=1 000,进化代数P=200.本例中取Pc分别为0.9和0.1,Pm分别为0.1和0.9,以做相互对比.

表1 每列车运送的换乘客流量数据(人)(平峰)Table 1 Transfer count of each train(non-peak-hours)

5.1.2 计算结果及分析

通过在Pentium 4双核处理器计算机(2.00 GHz主频,2 GB内存)上运行,各设置参数对应最优解及各代平均适应度f随代数的变化规律如图2 (a)～图2(d)所示.

图2 进化过程Fig.2 The evolutionary process

图2中(a)、(c)对应每代平均适应度值随代数变化基本在一个水平,这是由于变异概率Pm取值较大,使进化过程中每代均破坏了前一代种群接近最优解的积木块,主要依靠随机性搜索最优解,而(b)、(d)平均适应度基本随着进化代数呈现逐渐递增的态势,并最终趋于稳定,即种群中个体的综合水平不断提高.同时,由于采取精英保留策略,因此各图中最优解均呈现单调递减性.本文采用图(b)中对应参数Pc=0.9,Pm= 0.1计算.

通过对St1协调,计算获得一些优化解,对应各方向第一趟列车离站时刻如表2所示.作为对照,将式(13)改为f=F,则可以求得部分较劣解,如表3所示.需要指出的是表2、表3中只列出部分优化解和较劣解.

表2 St1站的协调优化解(平峰)Table 2 Optimal solutions in St1(non-peak-hours)

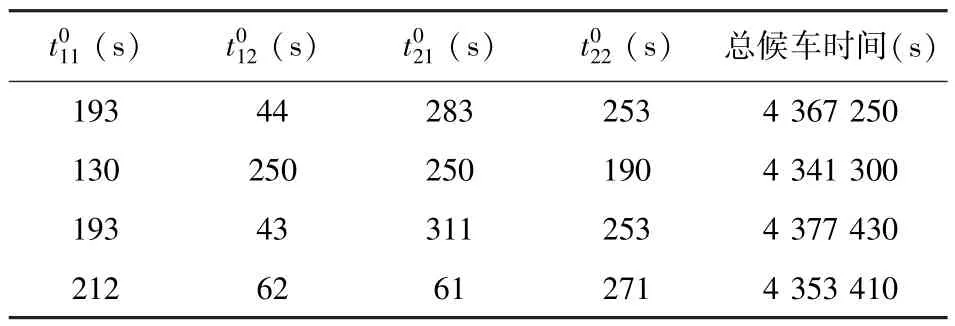
表3 St1站的协调较劣解(平峰)Table 3 Bad solutions in St1(non-peak-hours)

由于遗传算法使用概率搜索法,因此不易找出最优解,可以通过多次运算,对结果做筛选,并作为全局最优解.根据优化结果,假设取表2中第3行数据做为协调依据,则在协调时段内各线路各方向第1趟列车离开换乘站的时刻分别为:线路1上行为10:02,下行为10:01:59;线路2上行为10:03: 01,下行为10:03:01.以后各趟列车的离站时刻分别为在首趟车离站时刻的基础上各自增加本方向整数个行车间隔.以此为基础,利用区间运行时间及各站停站时间,可反推各线路列车在始发站的发车时刻.

5.2 早高峰时段案例

同理对早高峰时段7:00～9:00分析,设置各线路行车间隔h11=200 s,h12=180 s,h21=200 s, h22=190 s.线路间纯换乘时间均为100 s.停站时间D11=D12=45 s,D21=D22=40 s.客流量如表4所示.

表4 每列车运送的换乘客流量数据(人)(早高峰)Table 4 Transfer count of each train(morning-peak-hours)

计算过程同平峰时段案例,计算得出优化结果如表5,相对较劣的结果如表6.

表5 St1站的协调优化解(早高峰)Table 5 Optimal solutions in St1(morning-peak-hours)

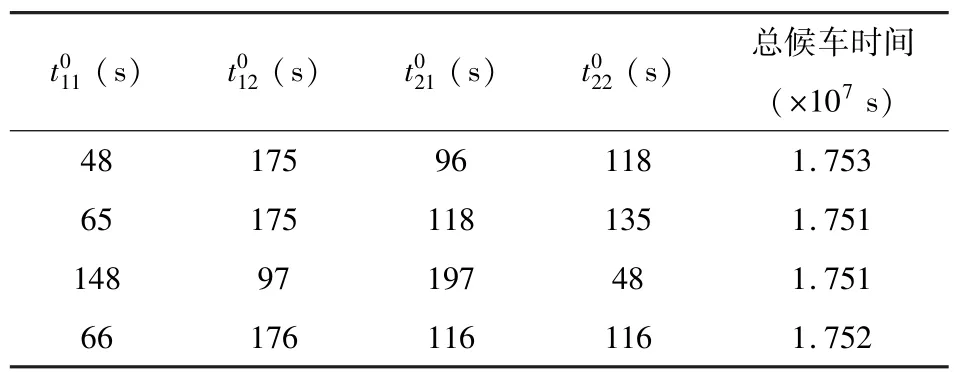
表6 St1站的协调较劣解(早高峰)Table 6 Bad solutions in St1(morning-peak-hours)

假设取表5中第1行数据做为协调依据,则早高峰时段各方向第1趟车离开换乘站的时刻分别为:线路1上行为07:01:02,下行为07:02:22;线路2上行为07:02:01,下行为07:01:11.以后各趟列车的离站时刻分别为在首趟车离站时刻的基础上各自增加本方向整数个行车间隔.

5.3 案例结果对比分析

根据表2和表3,平峰时段协调后,旅客换乘候车相对优化比率,即较劣解与较优解对应的总候车时间之差再与较劣解对应的总候车时间的比值,约为44%;而根据表5和表6,早高峰时段协调后,旅客换乘候车相对优化比率约为28%.同时还可以得出,影响协调效果的关键因素为协调时段内的客流量和行车间隔.客流量影响优化的绝对减小值,即较劣解与较优解对应的总候车时间之差,客流量越大,协调后旅客换乘总候车时间的绝对减小值就越大,即整体社会效益越明显;行车间隔影响优化的相对值,行车间隔越大,协调后旅客换乘候车时间相对优化比率就越大,即旅客服务水平提升幅度越大.

6 研究结论

本文分析了线路不同相交形式情况下换乘站存在换乘接续方向总数的计算方法;以换乘站旅客总换乘候车时间最少为目标建立了基于离站时刻协调的列车衔接优化模型,实现了列车在地铁换乘站的离站时刻优化调整;设计简单遗传算法,并对算例求解,结果验证了本模型能够减少旅客的换乘候车时间,具有一定的应用价值.本文只是研究了各列车在换乘站的离站时刻协调问题,而在网络中存在多个换乘站情况下,各换乘站之间的相互协调问题将作为进一步的研究内容.

[1] 周艳芳,周磊山,乐逸祥.城市轨道网络换乘站列车衔接同步协调优化研究[J].铁道学报,2011,33 (3):9-16.[ZHOU Y F,ZHOU L S,YUE Y X. Synchronizedandcoordinatedtrainconnection optimization for transfer stations of urban rail networks [J].Journal of the China Railway Society.2011,33 (3):9-16.]

[2] 张铭,杜世敏.基于递阶偏好的轨道交通网络化运营换乘协调优化[J].铁道学报,2009,31(6):9-14. [ZHANGM,DUSM.Transfercoordination optimization for network operation of urban rail transit based on hierarchical preference[J].Journal of the China Railway Society.2009,31(6):9-14.]

[3] 徐瑞华,张铭,江志彬.基于线网运营协调的城市轨道交通首末班列车发车时间域研究[J].铁道学报, 2008,30(2):7-11.[XU R H,ZHANG M,JIANG Z B. Study on departure time domain of the first and last trains of urban mass transit network based on operation coordination[J].Journal of the China Railway Society. 2008,30(2):7-11.]

[4] Rachel C,W Wong.et al.Optimizing timetable synchronization for rail mass transit[J].Transportation Science.2008, 42(1):57-69.

[5] Chung Min Kwan,C S Chang.Timetable synchronization ofmassrapidtransitsystemusingmutiobjective evolutionary approach[J].IEEETransactionson Systems,Man,and Cybernetics Part C:Applications and Reviews.2008,38(5):636-648.

[6] 孙鹏,赵佳虹,丁宏飞.基于换乘协调的城市轨道交通列车开行方案优化[J].铁道运输与经济,2011, 33(12):67-70.[SUN P,ZHAO J H,DING H F.The optimization of urban rail transit operation scheme based on coordinated transfer[J].Railway Transport and Economy.2011,33(12):67-70.]

[7] 徐宗本.计算智能(第一册)——模拟进化算法[M].北京:高等教育出版社,2005[XU Z B. Computational intelligence(1)—simulated evolutionary algorithm[M].Beijing:HigherEducation Press,2005.]

Optimization of Convergence based on the Coordination of Train Departure Time in the Subway Transfer Station

BAI Guang-zhenga,GUO Jina,SHI Hong-guob,YANG Yanga,ZHANG Tai-huaa
(a.School of Information Science and Technology;b.School of Traffic and Transportation, Southwest Jiaotong University,Chengdu 610031,China)

By coordinating the trains'departure time in the transfer station,optimized scheme is proposed to reduce the waiting time of transfer passengers in the transfer station of the urban traffic network.The transfer relationship between two trains in different lines which intersect with different forms in a transfer station is analyzed,and the formulas are derived to describe these connecting relationships.Based on the analysis,a model which minimizes the total waiting time of all transfer passengers during the coordinating period is established.Simple genetic algorithm(SGA)with the discard method is designed to solve this problem.Finally,an example with two lines'intersection is given to verify the model and partial optimized solutions are obtained by using the proposed algorithm.The results show that the model can reduce transfer passengers'waiting time.This study can provide some theoretical reference for the design and optimization of the train operation scheme under the urban traffic network operating scenario.

urban traffic;transfer connecting optimization;simple genetic algorithm;transfer station; coordination model

U292.4+1

: A

U292.4+1

A

1009-6744(2013)05-0134-07

2013-03-08

2013-06-09录用日期:2013-06-20

中央高校基本科研业务费专项资金资助(SWJTU11CX44);铁道部科技研究开发计划项目(2012X010-A).

白广争(1986-),男,山东曹县人,博士生.

*通讯作者:gj60@sina.com