港口物流综合效率测度研究

李电生,张圣泽*,员丽芬

(1.中国海洋大学经济学院,山东青岛266100;2.北京交通大学交通运输学院,北京100044)

港口物流综合效率测度研究

李电生1,张圣泽*1,员丽芬2

(1.中国海洋大学经济学院,山东青岛266100;2.北京交通大学交通运输学院,北京100044)

随着世界经济的衰退和我国经济结构的调整,各大港口之间的竞争正从以往的注重外延扩张向内涵式发展转变,从盲目追求吞吐量向提高综合效率转变.目前国内外港口物流的研究中缺乏对综合效率测度的研究,尤其是缺乏X-效率的测算分析.为此,本文在以往研究的基础上,构造了港口物流投入产出的效率测度指标体系,将DEA二次相对评价模型引入到港口物流效率测度中,以生产效率和X-效率测度值为基础,提出了测算综合效率的公式.最后利用此模型对我国13个港口进行了实证模拟,结果表明,该模型适用于港口物流效率的测度研究.

水路运输;港口物流;X-效率;综合效率;DEA二次相对评价;港口管理水平

1 引 言

港口作为海洋运输物流系统的节点枢纽,是连接多种运输方式的重要依托场所,一般认为,港口物流指港口以自身软硬件系统为核心,依托腹地公铁集疏运系统,向顾客提供特定的货物服务组合的综合物流系统.借鉴我国学者樊纲[1]提出的经济效率的概念——“经济效率是指社会利用现有资源进行生产所提供的效用满足的程度,因此也可一般地称为资源的利用效率”,本文中将港口物流效率定义为一种度量港口在基础设施、腹地经济和集疏运系统支撑下进行货物转换速度高低的指标.港口物流效率主要包括三个方面:生产效率、X-效率和综合效率,其中生产效率反映港口物流活动的投入产出能力,X-效率反映管理制度在港口物流中的作用,综合效率则是二者的有机结合,体现出港口的物流竞争力.随着经济全球化进程的加快和国际贸易量的不断增大,各个国家对港口的建设与运营日益重视,并将港口物流效率视为港口竞争力的主要指标,用来评价物流系统的资源配置效果.美国金融危机和欧债危机发生后,我国的对外贸易额不断下滑,对我国目前的港口转型产生了很大的不利影响,港口物流效率的测度问题成为国内外学者共同关注的热点问题.

国外学者初期主要利用单一指标衡量港口效率,Kim和Sachish[2]借助单个指标得到了港口的全要素生产率.到1993年Roll和Hayuth[3]首次应用DEA方法评价港口效率,解决了评价指标单一性的问题,但多指标评价时容易出现指标之间的冲突.于是一些学者应用综合评价方法从港口技术效率、规模效率等角度进行了更细致的研究: Cullinane等[4]固定港口投入量来测算实际产出与理论最大产出的距离值,测算出了港口的技术效率;钟铭、吕媛媛[5]利用灰靶模型对港口的经济效率进行了测度;庞瑞芝[6]利用DEA和Malmquist生产率指数对我国沿海主要港口的动态效率进行了评价,指出我国沿海港口投入/产出的比重过高.上述研究从技术效率、规模效率和纯技术效率三个方面对港口进行了效率测度,但却没有针对港口综合效率和X-效率的测度.

此后学者对港口物流效率测度的研究多集中在理论定义的阐述上,而针对效率测度的文献较少,也没有学者对中国港口的物流综合效率和X-效率进行实证研究.

基于以上分析,本文采用DEA二次相对评价模型,对中国13个大型港口的物流平均生产效率和X-效率分别进行测度,最终得到港口物流的综合效率.希望能够找到制约物流效率的限制因素,以便港口管理当局有针对性地制定相关政策,提高港口物流的生产效率和X-效率.

2 效率测度方法选择——DEA二次相对评价模型的适用性

影响港口投入产出效率的因素除了通常考虑的资源配置外,还有一些不明的低效率因素,主要是组织、动机等非市场因素,Leibenstein[7]据此提出了X-效率理论,将其定义为“除规模和范围影响之外的所有技术和配置效率,是关于整合技术、人力资源,以及其他资产来生产给定的管理水平的测定”.

测算X-效率的主要手段是前沿面分析,针对前沿面的分析方法主要分为两种.第一种是非参数线性规划方法,以A.Charnes[8]于1978年提出的数据包络分析法(DEA,data envelopment analysis)为代表.第二种是参数计量方法,以随机前沿分析方法(Stochastic Frontier Analysis,SFA)为代表.但这两种方法都是单独对生产前沿面进行分析,有着单一成本导向的弊端.冯英浚、李成红[9]在费莱尔测度方法和DEA方法的基础上提出了二次相对评价模型,以参考指数和当前指数代表评价单元不同时间点的状况,模型具有动态性,更贴近Leibenstein关于X-效率取决于组织和动机的论断.

本文试图将DEA二次相对评价模型应用于我国港口物流的综合效率评价,在分别对静态平均生产效率和动态X-效率测度的基础上,对港口物流综合效率进行合成.然而,DEA二次相对评价模型的关键在于采用什么方法来确定“指数状态”,以往文献多用AHP法测算指数状态,过于主观臆断.本文将采用DEA中的C2R模型来确定指数状态,以求得客观的效率指数状态前沿面,这样才能得到公正的港口物流X-效率测度.

3 港口物流综合效率测度体系构建

构建港口物流综合效率测度体系的基本思路为:

①确定港口物流效率评价指标体系;

②确定“指数状态集”,采用DEA的C2R模型确定“参考指数集”和“当前指数集”,分别表示基期和当期的港口物流投入产出效率;

③基于“指数状态集”,分别从静态和动态两个角度进行二次相对效率评价,即从静态的角度合成基期和当期的港口物流投入产出效率,实现生产效率测度,从动态的角度,将“参考指数集”和“当前指数集”分别作为输入输出集,利用DEA的BC2模型测算港口物流X-效率;

④引用综合效率测度公式将港口物流生产效率和X-效率进行合成,实现港口物流综合效率的测度(如图1所示).

图1 港口物流综合效率测度体系结构Fig.1 The system structure of comprehensive efficiency measurement of port logistics

3.1 评价指标体系的建立

本节讨论的港口物流效率测度的指标体系,基本结构来源于文献[2,4,5]的研究成果,经过分析改进将具体指标体系分为两层:第一层为准则层,由港口物流基础设施、物流支持、集疏运能力、港口物流规模、港口物流发展潜力5个准则组成;第二层为指标层,由11个指标组成,具体指标介绍见表1.

表1 港口物流效率测度指标体系表Table 1 The systematic figure of measurement index of port logistic efficiency

需要说明的是:起重机数量和堆场面积同样作为两个重要的输入指标,但是我们无法获得全面的数据;船舶在港停泊时间作为重要的输出指标,难以统一量化且各港口的物流信息网均不对外开放,因此最终确定选取表1中的11个指标来测度港口物流效率.

3.2 “参考指数集”DP与“当前指数集”DC的确定

假设对n个港口的港口物流投入产出效率进行评价,则每一个港口为一个决策单元DMU.每个DMU都有m种类型的输入(表示对资源的耗费)以及s种类型的输出(表示成效的产出量),Xj= [x1j,x2j,…,xmj]T(j=1,2,…,n)为第j个决策单元的m维投入向量,…,n)为第j个决策单元的s维输出向量.根据Charness[8]所提出的传统C2R模型①C2R模型计算规模报酬不变时每一个决策单元DMU的投入产出总效率,包含纯技术效率和规模效率.,引入松弛变量S-和S+,测算出第j个港口(决策单元DMU)的投入产出效率,对于第j0个决策单元DMUj0的DEA模型线性规划表述为

式中 Xj0表示第j0个DMU输入向量;Yj0表示第j0个DMU输出向量;θ表示投入产出效率值;λ表示决策单元线性组合的系数.若θ*=1,S-*=S+*=0,则称j0单元为DEA有效;若θ*=1,S-*,S+*存在非零值,则称j0单元为DEA弱有效;若θ*＜1,则称j0单元为DEA无效.设t=P,C分别表示基期和当期,将基期第j个DMU的投入产出效率称为第j个港口的“参考指数”,以表示,所有的港口基期“参考指数集”用DP表示;将当期第j个DMU的投入产出效率称为第j个港口的“当前指数”,以表示,同样以DC表示“当前指数集”;(DP, DC)即为指数状态集.

3.3 二次相对评价的测算

(1)静态生产效率测算.

生产效率主要从静态角度反映港口投入产出关系.由此,第j个港口的静态效率由相应的“参考指数”和“当前指数”的平均数合成确定:

(2)动态X-效率测算模型.

港口物流X-效率是在消除客观基础条件的情况下,动态地反映各港口物流的管理水平.将前面所测算得到的港口物流基期的绩效综合指数作为各港口物流基础条件的一种度量,看做一种输入;而将港口物流当期的绩效综合指数看做一种输出,称数组为第j个港口物流效率的指数状态,称凸集

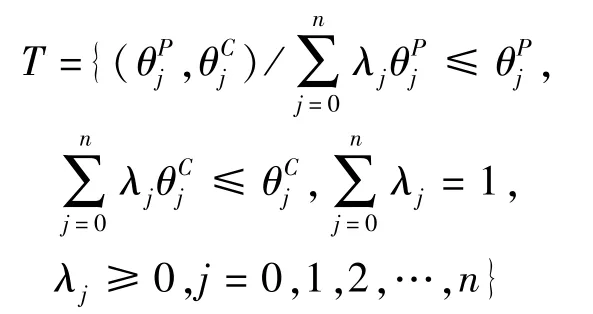
3.4 综合效率的合成

本文根据港口物流生产效率和X-效率的特点,提出港口物流综合效率的测度公式.

式中 δ为港口物流综合效率;αj为基于静态的港口物流生产效率;βj为动态的港口物流X-效率.

4 中国港口物流综合效率测度实证模拟

4.1 样本的选取

根据《2008年中国港口综合竞争力指数排行榜》,本文选取了排行榜的前13名,即宁波港②2006年起,“宁波港”正式与“舟山港”合称为“宁波舟山港”,为保持数据一致性,本文2006、2011年指标采用宁波港域和舟山港域的数据之和,继续使用“宁波港”的名称.、上海港、青岛港、天津港、广州港、深圳港、大连港、连云港港、营口港、厦门港、烟台港、日照港和苏州港.这13个港口地处我国港口物流发展最为发达的地区,2011年,这13个港口完成的集装箱吞吐量占全国的83.79%,货物吞吐量占到45.03%,因此它们基本可以代表我国港口发展最前沿的情况.

港口投资回收期一般为5年,同时我国港口规划也是5年一次.若要测算动态效率提升程度,必须采用间隔5年的数据.本文采用了2006年底和2011年底的横截面数据,样本数据主要来源为2007年、2012年的《中国统计年鉴》及《中国海洋年鉴》,各港口所在城市及经济腹地城市历年统计公报,《公路水路交通运输行业发展统计公报》,《中国港口发展报告》等.

4.2 我国13大港口物流“指数状态”测算分析

由于DEA模型对样本数量要求很高,当样本有限时会导致DEA有效的DMU过多,得不到有效的区分.为了克服这一不足,本文通过设置一个虚拟的最佳DMU,使得原来效率指数相同的DMU相对于虚拟的最佳DMU变得非有效,来达到比较效率指数相同DMU差异程度的目的.令输入和输出指标数据为xi=min xij,yr=max yrj(i=1,2…,m; r=1,2…s;1≤j≤n);xn+1=(x1,x2,…,xm)T, yn+1=(y1,y2,…,ys)T,则称这个以xn+1和yn+1为输入和输出的决策单元n+1,是这n个决策单元的虚拟DMU*,也就是最佳DMU,把DMU*并入到实际的n个决策单元中,就可得到基于最佳DMU的DEA扩展模型.

本文运用DEA扩展模型和DEAP软件进行计算,得到2006年和2011年底港口物流的投入产出效率水平测度,如表2所示,将两年的crste效率值分别作为“参考指数”和“当前指数”.

表2 我国13港口物流投入产出效率水平测度Table 2 The level measurement of input-output efficiency of port logistics in China

基期和当期13个港口的2006年“参考指数”和2011年“当前指数”分布情况如图2所示.

4.3 我国13大港口平均生产效率、X-效率和综合效率测算分析

根据表2测算出的13个港口2006年和2011年的指数值,采用DEA二次相对评价法,可以计算出对应的平均生产效率、X-效率和综合效率,结果见表3.

港口物流X-效率与平均生产效率考察的侧重点是不同的,X-效率侧重于投入产出效率的提升程度,从动态角度扣除了自然基础条件的不同,从而可以客观地反映港口的管理水平,而不仅仅是由于配置不同或腹地不同而导致的低效率,这也是有些学者直接用X-效率代表管理水平高低的原因.而综合效率则能够反映出港口整体的生产和管理水平的高低.

图2 我国13大港口物流“参考指数”和“当前指数”分布图Fig.2 The distribution curve of the“reference index”and“current index”of the thirteen big port logistics in China

表3 我国13港口物流的平均生产效率、X-效率和综合效率Table 3 The average production efficiency,X-efficiency and comprehensive efficiency of port logistics of China’s 13 ports

图3 我国13大港口的生产效率、X效率和综合效率对比图Fig.3 The distribution chart of average production efficiency,X-efficiency and comprehensive efficiency of China's 13 major ports in 2011

从图3可以清晰地看出,生产效率最低的是广州港,这与港口综合竞争力指数③国际海运网、大连海事大学世界经济研究所、中国港航研究院:《2008中国港口综合竞争力指数排行榜报告》.的研究结果并不一致,主要原因在于:竞争力指数侧重于港口规模、吞吐量等绝对量的比较;而本文从效率的角度出发,要求要以最小的投入得到最大的产出,更重视相对量的测度,生产效率较高的港口为宁波港、烟台港、日照港和苏州港.但是烟台港、日照港、深圳港和苏州港的X效率值较低,说明港口的管理水平有待提高.我国主要港口物流的X-效率在0. 3—0.8之间,然而,生产效率相对较高的深圳港的X-效率却仅仅为0.33,与其在我国港口综合竞争力指数排行榜上第6位的地位不相符.其原因主要是受金融危机的影响,在金融危机爆发之前的高产出造成了深圳港的高基础,深圳港的基础设施得到了很大改善,但却由于金融危机的爆发没有得到应有的产出,过高的基期“参考指数”导致其X-效率值很低.

综合效率方面,我国13大港口的综合效率值均在0.2-0.4之间.虽然上海港的集装箱吞吐量是最高的,但最终计算的综合效率仅为0.236.作为2011年货物吞吐量排名第一的宁波港,其综合效率仅为0.283,是因为宁波港近年来投资建设的基础设施比较多,导致港口投入产出效率降低,同时港口扩张导致管理有效性降低,造成X-效率低下.虽然宁波港现在综合效率较低,但加大基础设施投资的决策从长远来看是具有前瞻战略性的,随着经济的进一步发展,宁波港优良的硬件设备将发挥更大的作用,效率必将得到提升.

由测算结果可知,我国港口2011年的投入产出效率普遍比2006年高,说明这五年各港口都得到了快速发展,但X-效率基本都在0.8以下,个别港口仅在0.3左右,说明国内港口在追求高投入高运量的同时,忽视了管理水平的提高.在这两个效率值的基础上,我国港口物流的综合效率也普遍偏低,与国外港口相比,我国港口还处于粗放发展的阶段.但是,我国港口物流大部分都处于规模报酬递增状态,说明港口还处于快速增长阶段,发展空间很大.

5 研究结论

本文的核心内容为三个港口物流效率指标的测度:首先,在以往文献的基础上,构造了一个港口物流投入产出的效率测度指标体系,并在此基础上,应用DEA中C2R模型测度了港口物流的生产效率值;其次,将相隔五年的港口物流生产效率值分别作为“参考指数”和“当前指数”,确定指数状态集后运用DEA中BC2模型测度了港口物流的X -效率值;第三部分,基于港口的生产效率和X-效率,计算出了港口物流综合效率.最后,应用这个模型对我国13个竞争力最强的港口进行了实证模拟.

对我国港口物流的X-效率测度的研究弥补了国内关于此项研究的空白,本文更多的是提供一种思路,但影响港口物流效率的因素相当复杂,篇幅所限不能一一涉及,模型应用仍不是很成熟,这是本文的局限所在.但是,从用DEA二次评价法测度X-效率的角度去思考同类问题,对于效率测度的理论和实践是大有裨益的.

[1] 纲.市场机制与经济效率[M].上海:上海三联书店, 1992.[FAN G.Market mechanisms and economic efficiency[M].Shanghai:JointPublishing (Shanghai),1992.]

[2] Kim M,Sachish A.The structure of production:Techical change and productivity in a port[J].Journal of Industrial Economics,1986(35):209-223.

[3] Rolly,Hayuth Y.Port performance comparison applying data envelopment analysis(DEA)[J].Maritime Policy and Management,1993(20):153-161.

[4] Cullinane K,Wang T.A comparison of mathematical programming approaches to estimating container port produntion efficiency[J].Journal of Productivity Analysis,2006(24):73-92.

[5] 钟铭、吕媛媛.基于灰靶模型的港口效率评价[J].大连海事大学学报,2007(6):130-132.[ZHONG M, LV Y Y.Efficiency evaluation of ports based on grey target model[J].Journal of Dalian Maritime University, 2007(6):130-132.]

[6] 庞瑞芝.我国主要沿海港口的动态效率评价[J].经济研究,2006(6):92-100.[PANG R Z.Dynamic efficiency evaluation of China's major coastal ports[J]. Economic Research Journal,2006(6):92-100.]

[7] Leibenstein H.Allocative efficiency vs.X-efficiency[J]. American Economic Review,1966(56):392-415.

[8] Charness A,Cooper W W.Measuring the efficiency of decision making unit[J].European Journal of Operational Research,1978(3):338-339.

[9] 冯英浚、李成红.二次相对效益——衡量企业经济效益的一种新指标[J].中国软科学,1995(7):30-37. [FENG Y J,LI C H.Secondary relative benefits—a new index to measure economic efficiency of enterprises [J].China Soft Science,1995(7):30-37.]

Research on Measurement of Comprehensive Efficiency for Port Logistics

LI Dian-sheng1,ZHANG Sheng-ze1,YUAN Li-fen2
(1.School of Economics,Ocean University of China,Qingdao 266100,Shandong,China; 2.School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

The competition among the ports is changing from focusing on extension to focusing on inner development,and from blindly pursuing throughput to improving overall efficiency,along with the decline of the world economy and the adjustment of China's economic frame.In order to counterbalance the slow development of research on measurement of overall efficiency in port logistics,especially on the measurement analysis of X-efficiency,this paper demonstrates a KPI,which is a measurement of efficiency that deals with the investment and return on investment in port logistics,and introduces DEA quadratic relative evaluation model to measure port logistic efficiency.On the basis of production efficiency and measurement analysis of X-efficiency,this paper put forward a formula to measure the overall efficiency,which supplies a gap in this research.In the end,this paper uses this model to give a demonstration to simulate the relevant operation in 13 ports of China,and the result validates that this model is applicable and appropriate to measure the efficiency of port logistic.

waterway transportation;port logistics;X-efficiency;comprehensive efficiency;DEA twostage relative evaluation;port management level

F253.9

: A

F253.9

A

1009-6744(2013)05-0107-07

2013-05-03

2013-06-10录用日期:2013-6-20

李电生(1966-),男,河北石家庄人,副教授.

*通讯作者:zhangshengze90@hotmail.com