基于M/M/s模型的高速铁路车站售票窗数量分析

孙年友

(广州铁路(集团)公司科研所,广州510080)

基于M/M/s模型的高速铁路车站售票窗数量分析

孙年友*

(广州铁路(集团)公司科研所,广州510080)

揭示了高速铁路车站旅客排队购票问题的特征,发现其符合M/M/s模型的假设条件.基于M/M/s模型,建立了售票窗数量的分析模型.结合广州南站调研数据,计算了不同旅客到达率下的售票窗最少配置数,并研究了队列长和等待时间与旅客到达率的关系.结果表明∶售票窗的最少配置数由旅客的到达率和售票窗的售票率决定.在配置最少的售票窗和0.86人/min的售票率下,随着旅客到达率的提高,队列长和等待时间均呈现以6为周期的周期性变化.在每个周期内,两个指标均不断增加,最终的峰值由到达率和售票率之比与售票窗最少配置数的接近程度决定.在较低的旅客到达率下,不同售票率下需要配置的最少售票窗数差别不大,而随着到达率的提高,这种差距会逐渐扩大.

铁路运输;售票窗数量;M/M/s模型;高速铁路车站;到达率

1 引 言

随着社会经济的发展,居民的时间价值不断提高,快速性在旅客选择出行方式时考虑的诸多因素中越来越重要.近年来,不断投产运营的高速铁路为中长途旅客的出行提供了又一选择,而不断增长的客流量对车站内售票设备的配置造成了较大压力,部分车站售票厅内甚至出现了拥堵及长时间排队现象.这种现象影响了高速铁路快速性优势的充分发挥,在一定程度上降低了高速铁路的吸引力.因此,对高速铁路车站的售票窗数量进行研究和分析具有重要意义.

排队论是研究随机服务系统工作过程的重要数学理论和方法,而交通运输领域内的很多系统都可以视为随机服务系统,例如,高速公路检修区的排队等待现象[1]、铁路列车的股道分配过程[2]、城市公交的进站停车过程[3]、地铁车站乘客经过楼梯和通道的疏散过程[4]等,这些问题都可以采用排队论进行较好地描述和解决.针对售票窗的配置问题,廖明军等[5]采用元胞自动机模型模拟了行人的排队购票行为,并在模型中嵌入了排队论中的转移概率函数,这种方法能较好地分析队列长等指标和售票窗数量的关系,但难以确定在不同的行人到达率和售票率下所应配置的具体的售票窗数量;李季涛和孙全欣[6]建立了基于排队论、带有止步和中途退出的铁路客运站售票厅排队系统的微观仿真模型,该模型考虑到了旅客购票过程中的行为特性,但需要大量的基础数据支撑,而一旦获取的数据与真实情况不符,这种考虑反而容易造成较大的误差;李得伟等[7]基于旅客行为的微观仿真,以北京南站为例,研究和评估了大型铁路客运站售票设备的配置方案,这种方法在刻画售票设备与旅客的相互作用方面更为精细,但该方法的建模过程较复杂,模型移植到其它案例的代价较高.

本文基于排队论中的M/M/s模型,建立了高速铁路车站售票窗配置数量的计算模型,该模型视系统中的旅客具有相同的购票行为,并遵循先到先服务的排队规则.然后,结合广州南站的实际调研数据,计算了不同旅客到达率下售票窗的最少配置数量,分析了在配置最少售票窗的情况下,系统的队列长和等待时间与旅客到达率的关系,模型可以移植到其它高速铁路车站售票窗配置数量的计算中.

2 旅客排队购票问题分析

旅客排队购票问题由两个过程构成,旅客来到车站要求购买车票及车站售票窗售票.旅客与售票窗(包括人工售票窗口和自动售票机)构成一个排队系统,称为随机售票系统.在这个系统中,缺少旅客或售票窗任何一方都不会构成排队系统.系统中每一名旅客的购票过程需要经过如下步骤:旅客到达、排队等待、购票和离去,如图1所示.

图1 旅客排队购票过程示意图Fig.1 The sketch process of passengers waiting in queue for buying tickets

这种排队系统由3个基本部分组成:输入过程、排队及排队规则、售票机制,并且具有如下特征:

①旅客到达的间隔时间通常是相互独立的,并且服从Poisson分布;

②排队规则是等待制,即旅客到达时,若所有售票窗均被占用,就排队等待,旅客按照到达的先后顺序接受售票;

③售票时间通常服从负指数分布;

④售票窗的数量通常为多个,并且工作相互独立.

上述特征符合M/M/s模型的假设条件[8],因此,本文采用该模型来研究和分析高速铁路车站售票窗数量对旅客购票的影响.同时,可以认为售票厅内空间无限,并且一直存在购票的旅客,该模型可以进一步假设为M/M/s/∞/∞模型.

3 售票窗数量分析模型的构建

旅客到达过程遵循的Poisson分布的参数为λ,即单位时间内旅客的到达人数为λ;售票时间遵循的负指数分布的参数为μ,即单位时间内售票窗售出的票数为μ;系统内有s个售票窗,各售票窗的工作相互独立,当系统中有n个旅客时,整个系统的售票率为sμ(当n≥s)或nμ(当n＜s).

系统的售票强度ρ为

售票厅内无旅客购票,即系统空闲的概率P0为

系统中有n个旅客的概率Pn为

排队系统状态概率的平衡方程为

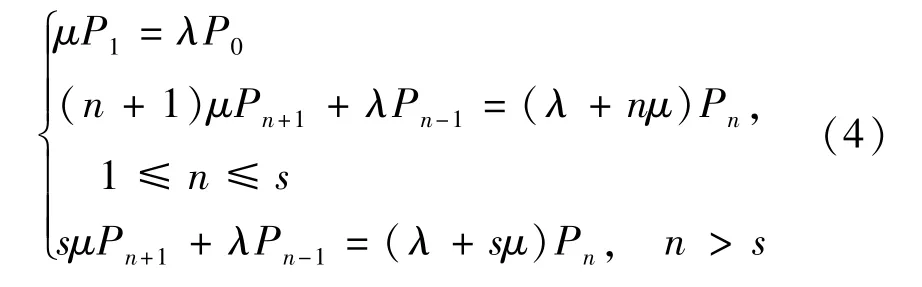
式中 P1为系统中有1个旅客的概率;分别为系统中有n-1、n+1个旅客的概率.

旅客购票需要等待的概率Pq为

系统中排队等候的旅客数,即平均队列长L为

旅客在系统中的平均等待时间Wq为

为保证排队系统持续稳定运转,车站售票窗开启数s必须满足售票强度[8],即

满足条件的最小s即车站售票窗最少配置数.

4 广州南站售票窗数量分析

广州南站为特等客运站,是武广高铁、广珠城际及在建的贵广高铁、南广高铁、广佛肇城际的交汇点.站房总建筑面积达48.6万m2.2011年日均旅客发送量约8万人次,2012年增长至9万人次,其中,到广州南站购票的旅客日均在3万人次以上.

根据调查,广州南站旅客在自动售票机上的平均购票时间为80 s,自动售票机的平均售票率为0.75人/min;旅客在人工售票窗口上的平均购票时间为70 s,人工售票窗口的平均售票率为0.86人/min.

本文的平均售票率μ取0.86人/min,广州南站不同旅客到达率λ下的最少售票窗配置数s如表1所示,表1同时给出了在旅客到达率为λ、售票窗数量为s的情况下,整个购票系统的队列长和旅客的等待时间.

表1 不同旅客到达率和售票窗最少配置数下的队列长和等待时间Table 1 Queue length and waiting time with varied arrival rates and minimum ticket windows

从表1可以查询不同旅客到达率下售票厅应开启的售票窗数,售票窗是自动售票机和人工售票窗的总和.从表1可以看出,虽然设置最少售票窗数可以保证整个购票过程的持续稳定进行,但是到达率和售票率之商,即λ/μ,越接近于s,系统的平均队列长和旅客的平均等待时间越长,如旅客到达率λ=6人/min、售票率μ=0.86人/min、s=7时, λ/μ≈6.9767,接近于s,队列长达到了297.00,旅客平均等待时间达到了49.50 min;而当旅客到达速率λ=12人/min、售票率μ=0.86人/min、s=14时,λ/μ≈13.953 5,相对于上一种情形下距离s略远,队列长也有所下降,为295.65,旅客平均等待时间下降为24.64 min.

在售票率μ取0.86人/min并在设置最小售票窗数的情况下,系统的平均队列长和旅客的平均等待时间随旅客到达率的变化规律如图2所示.

图2 队列长(a)和等待时间(b)随旅客到达率的变化规律Fig.2 The influence of passengers'arrival rate on queue length(a)and waiting time(b)

从图2可以看出,随着旅客到达率的增加,系统的平均队列长和旅客的平均等待时间均呈现周期性的变化规律.

图2(a)中,周期为6,从1人/min开始,在每个变化周期内,系统的平均队列长随着旅客到达率的升高而增加,每个周期内的最低点为λ/μ(到达率和售票率之商)距离s(最小售票窗数)最远的点,最高点为λ/μ最接近于s的点.在每个周期内,前5个到达率下的平均队列长均低于后续周期内的对应点,而每个周期的峰值也略有降低,这主要是由于λ/μ距离s的远近造成的.另外,随着旅客到达率的升高,虽然在一个周期内,系统总体队列长的峰值降幅不大,但由于售票窗数是增加的,平均每队的队列长降低较为显著.

图2(b)中,周期也为6,在每个周期内,旅客的平均等待时间随着旅客到达率的增加而增加,但是每个周期内旅客平均等待时间的峰值衰减较为明显,这主要也是由λ/μ与s的相对大小造成的,每个周期内的前5个点相对于后续周期内的对应点变化不大.

一般来说,旅客购票时占用售票窗的时间越少,需要配置的售票窗也越少.根据调查,广州南站中,广深港和广珠城际售票窗的平均售票时间较短,约45 s,即μ=1.33人/min,而京广线售票窗的平均售票时间较长,约80 s,即μ=0.75人/min.本文分别取μ为0.75、0.86、1.00、1.20、1.33人/min时,售票窗的最少配置数与旅客到达率的关系如图3所示.

从图3可以看出,随着旅客到达率的增长,不同售票率下的售票窗最少配置数均是增长的.当μ=1.00人/min时,旅客的到达率每增加1人/min,需要配置的最少售票窗数便增加1个;当μ＞1.00人/min时,售票窗最少配置数的增长低于旅客到达率的增长;而当μ＜1.00人/min时,售票窗最少配置数的增长会高于旅客到达率的增长.在较低的旅客到达率(λ＜5人/min)下,不同售票率下的售票窗最少配置数的差距不大,随着旅客到达率的提高,这种差距逐渐扩大.

图3 售票窗最少配置数与旅客到达速率的关系Fig.3 The relationship between the minimum ticket windows and passengers'arrival rate

5 研究结论

高速铁路车站旅客排队购票问题符合M/M/s模型的特征,因此,本文采用M/M/s模型来研究高速铁路车站售票窗数量的配置问题.通过结合广州南站的实际调查数据,本文得到的主要结论如下.

售票窗的最少配置数是由旅客的到达率和售票窗的售票率决定的.在配置最少的售票窗和售票率为0.86人/min的情况下,广州南站排队购票系统的队列长和旅客平均等待时间随着旅客到达率呈周期性的规律变化,变化周期为6,每个周期内两个指标均是增长的,峰值的大小由到达率和售票率之商与最少售票窗数的接近程度决定.

当售票率高于1人/min时,最少售票窗数的增长低于旅客到达率的增长;当售票率低于1人/min时,最少售票窗数的增长高于旅客到达率的增长.在较低的旅客到达率下,不同售票率下的售票窗最少配置数的差距不大,随着旅客到达率的提高,这种差距会逐渐扩大.

[1] Tae Son Y.Queueing delay models for two-lane highway work zones[J].Transportation Research Part B: Methodological,1999,33(7):459-471.

[2] Wendler E.The scheduled waiting time on railway lines [J].Transportation Research Part B:Methodological, 2007,41(2):148-158.

[3] 苏国辉,吴群琪.基于排队论的线路密集点公交站台容量优化模型[J].交通运输系统工程与信息, 2011,11(6):164-168.[SU G H,WU Q Q.Capacity optimization of line-dense bus-stop by queuing theory [J].Journal of Transportation Systems Engineering and Information Technology,2011,11(6):164-168.]

[4] 陈绍宽,刘爽,肖雄,等.基于M/G/c/c模型的地铁车站楼梯通道疏散能力瓶颈分析[J].铁道学报, 2012,34(1):7-12.[CHEN S K,LIU S,XIAO X,et al.M/G/c/c-based model for passenger evacuation capacity of stairs and corridors in metro stations[J]. Journal of the China Railway Society,2012,34(1): 8-12.]

[5] 廖明军,孙剑,王凯英.基于元胞自动机模型的行人排队行为模拟[J].交通运输系统工程与信息, 2009,9(3):140-145.[LIAO M J,SUN J,WANG K Y.Simulation of queuing behavior based on cellular antomata model[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(3): 140-145.]

[6] 李季涛,孙全欣.铁路客运站自动售票机终端配置微观仿真分析[J].中国铁道科学,2011,32(5): 117-122.[LI J T,SUN Q X.Microscopic simulation analysis on the deployment of TVM terminal device in railway passenger station[J].China Railway Science, 2011,32(5):117-122.]

[7] 李得伟,禹丹丹,张彦,等.基于旅客行为微观仿真的大型铁路客运站售票设备配置方案评估研究[J].铁道学报,2013,35(2):1-7.[LI D W,YU D D, ZHANG Y,et al.Assessment of fare collection system of large-scalerailwaypassengerstationsbasedon microscopic simulation of passenger behavior[J]. Journal of the China Railway Society,2013,35(2): 1-7.]

[8] 郑大钟,赵大川.离散事件动态系统[M].北京:清华大学出版社,2000.[ZHENG D Z,ZHAO D C. Discrete event dynamic system[M].Beijing:Tsinghua University Press,2000.]

Quantities of Ticket Windows in High-speed Railway Stations Based on M/M/s Model

SUN Nian-you
(Guangzhou Railway(Group)Corporation Science&Technology Research Institute,Guangzhou 510080,China)

The characteristics of passengers waiting in queue for buying tickets in high-speed railway stations are revealed and these characteristics meet the assumptions of M/M/s model.Based on M/M/s model,an analysis model on quantity of ticket windows is established.The minimum ticket windows are calculated under varied passengers'arrival rates according to the investigation data in Guangzhou South Station.The relationship between queue length,waiting time and arrival rate is also discussed.The results demonstrate that the minimum ticket windows are determined by passengers'arrival rate and ticket windows' selling rate.The queue length and waiting time are both in a cycle increase with the rise of arrival rate when configuring the minimum ticket windows and selling 0.86 tickets per window and minute.The cycle period is 6 and the final peak is decided by the approximation of the division between arrival rate and selling rate to the minimum ticket windows.The difference in the configuration of minimum ticket window with varied selling rate is insignificant under lower arrival rate,but it will extend with the increase of arrival rate.

railway transportation;quantity of ticket windows;M/M/s model;high-speed railway station;arrival rate

U293.2+2

: A

U293.2+2

A

1009-6744(2013)05-0174-05

2013-02-19

2013-05-25录用日期:2013-06-18

孙年友(1962-),男,湖南耒阳人,高级工程师,硕士.

*通讯作者:sunconn@163.com