一类分数阶差分方程解的吸引性

张瑜， 孙明哲， 何延生

（延边大学理学院 数学系，吉林 延吉133002）

一类分数阶差分方程解的吸引性

张瑜， 孙明哲， 何延生＊

（延边大学理学院 数学系，吉林 延吉133002）

研究了一类分数阶差分方程解的吸引性．首先给出该问题的解的表达式，将该问题转化为一个算子的不动点问题．其次利用Schauder不动点定理，证明了解的存在性，并建立了该差分方程具有吸引性的充分性条件．最后将主要结果推广到中立型分数阶差分方程上．

吸引性；分数阶差分方程；初值问题；Schauder不动点定理

在过去的几十年中，分数阶微分方程已得到广泛的研究和应用，如在物理、动力学、化学、工程学等方面［1－2］．分数阶差分方程研究是较新的研究领域，近年来才逐渐取得一些成果，例如文献［3］研究了分数阶差分方程的初值问题，文献［4－6］研究了分数阶差分方程解的存在性问题，文献［7－9］研究了带有边值条件的非线性分数阶差分方程的问题．有关分数阶差分方程解的吸引性少有报道，本文将对此进行研究．

考虑分数阶差分方程初值问题（IVP）

其中Δα表示α阶分数差分算子，0＜α＜1，t∈N0＝｛0，1，2，…｝．f（t＋α－1，·）∶J×R→R是1个连续泛函，其中记C（J，R）表示J→R映射的全体．同时是1个巴拿赫空间，其范数定义为

1 预备知识

定义1［10］设ν＞0，函数f的ν阶分数和定义为，同时定义函数f的ν阶分数阶差分为．其中t∈Na＋N＋ν，且N∈N，0≤N－1＜ν≤N．

定义2［11］假设x（t）＝0是初值问题的解，且对应方程的任一解x（t），若则称方程的零解是吸引的．

定义3［10］对于任意的t和α，有，且规定如果t＋1－α是Γ函数的极点，同时t＋1不是Γ函数的极点，那么

引理1［10］设t和ν是任意的数，并且有定义，那么

引理2［4］设0≤N－1＜ν≤N，对任意的ci∈R，1≤i≤N，那么

引理3［11］（Schauder不动点定理）若X是巴拿赫空间，U是X的非空有界凸闭子集，并且T∶U→U是完全连续的，那么T在U中至少有1个不动点．

2 分数阶差分方程解的存在性及吸引性

为方便设Lp（J，R）是Lp空间且满足条件（H0）是连续的．

引理5 假设条件（H0）和如下条件（H1）成立，

（H1）存在1个常数γ1＞0，有

那么初值问题（1）至少有1个解x∈C（J，R）．

i）A是S1到S1的1个映射．对于t≥α－1，由条件（H1），有即

iii）AS1是等度连续的．设t1，t2≥α－1和t1＞t2，t1，t2∈Nα－1．分3种情况证明：

① 如果t1，t2∈ ［α－1，T］Nα－1，A是有限的和算子，因此A是1个平凡完全连续算子，AS1也是等度连续的．

② 如果t1，t2∈NT＋1，那么

定理1 假设条件（H0）和（H1）成立，则初值问题（1）的零解是吸引的．

证明 由引理5知，初值问题（1）的解存在且在S1中，在S1中所有函数x（t）→0，t→∞．因此，当t→∞时，初值问题（1）的解趋近于0．

引理6 假设条件（H0）和如下条件（H2）成立，

（H2）存在1个常数γ2，使得

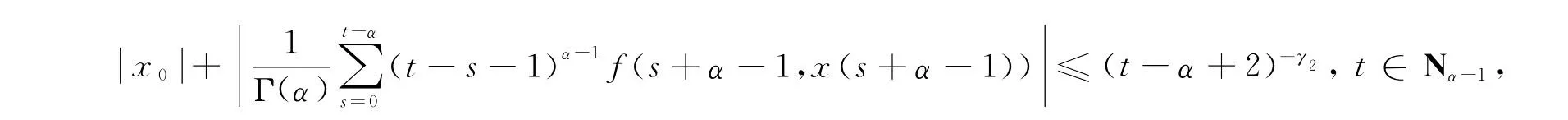
那么初值问题（1）至少有1个解x∈C（J，R）．

那么AS2⊂S2．剩下部分与引理5类似，故省略．

定理2 设条件（H0）和（H2）成立，那么初值问题（1）的零解是吸引的．

证明与定理1的证明类似，故省略．

引理7 假设条件（H0）成立且存在常数γ3＞0及y ∈C（J，R），使得如下条件成立，且y（t）满足条件有1个常数α2∈（0，α），使得y∈L1/α2（J，R＋），那么初值问题（1）至少有1个解x∈C（J，R）．

所以AS3⊂S3．剩下部分与引理5的证明类似，故省略．

定理3 设条件（H0）和（H3）成立，那么初值问题（1）的零解是吸引的．

证明与定理1的证明类似，故省略．

3 分数阶中立型差分方程解的存在性及吸引性

考虑分数阶中立型差分方程

其中0＜α＜1，t∈N0＝｛0，1，2，…｝．在条件（H0）下，类似于前面的证明有如下结论：

定理4 假设条件（H0）成立，且以下条件成立∶有1个常数使得是完全连续的，那么初值问题（2）至少有1个解x∈S′1，同时这个解具有吸引性，其中

定理5 假设条件（H0）成立，且以下2个条件成立：（H′3）存在1个常数γ′2＞0使得是完全连续的，那么问题（2）至少有1个解x∈，同时这个解具有吸引性，其中

定理6 假设条件（H0）成立且存在y′∈C（J，R），对任意的t∈Nα－1，k1∈R并且x∈C（J，R），存在常数γ′3满足如下条件满足条件：①有常数l2＞0使得有1个常数α2∈（0，α），使得是完全连续的，并

且存在常数l3＞0，k2∈R使得那么问题（2）至少有1个解x∈S′3，并且这个解具有吸引性．其中k1＋k2＝1，l2＋l3＜1，

［1］ Kilbas A A，Srivastava H M，Trujillo J J．Theory and applications of fractional differential equations［M］．Amsterdam：Elsevier Science，2006．

［2］ Miller K S，Ross B．AnIntroduction to the fractional calculus and differential equations［M］．New York：John Wiley，1933．

［3］ Atici F M，Eloe P W．Initial value problems in discrete fractional calculus［J］．Proc Amer Math，2009，137（3）：981－989．

［4］ Christopher S Goodrich．Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions［J］．Comput Math Appl，2011，61：191－202．

［5］ Christopher S Goodrich．Existence of a positive solution to a system of discrete fractional boundary value problems［J］．Appl Math Comput，2011，217：4740－4753．

［6］ Chen F，Luo X，Zhou Y．Existence results for nonlinear fractional difference equation［J］．Adv Difference Equ，Article ID 713201，2011．

［7］ Christopher S Goodrich．On discrete sequential fractional boundary value problems［J］．J Math Anal Appl，2012，383：111－124．

［8］ Atici F M，Eloe P W．Two－point boundary value problems for finite fractional difference equations［J］．J Difference Equ Appl，2010，17（4）：445－456．

［9］ Deng W．Smoothness and stability of the solutions for nonlinear differential equations［J］．Nonlinear Anal，2010，72：1768－1777．

［10］ Atici F M，Eloe P W．A transform method in discrete fractional calculus［J］．Int J Difference Equ，2007（2）：165－176．

［11］ 时宝，张德存，盖明久．微分方程理论及其应用［M］．北京：国防工业出版社，2005：10－13，302－304．

［12］ Atici F M，Sengul S．Modeling with fractional difference equation［J］．J Math Aral Appl，2010，369：1－9．

Atrractivity of a class of fractional difference equations

ZHANG Yu， SUN Ming－zhe， HE Yan－sheng＊
（Department of Mathematics，College of Science，Yanbian University，Yanji 133002，China）

We study attractivity of a class of fractional difference equations．Firstly we give a expression of the solution of fractional difference equations．And，this solution is converted into a discussion about fixed points for a operator．Secondly，we prove existence of solutions by using Schauder fixed point theorem．And we establish the suffi－cient conditions that proves attractivity of fractional order difference equations．Finally，the main results are extended to fractional neutral difference equtions．

attractivity；fractional difference equations；initial value problem；Schauder fixed point theorem

O175

A

1004－4353（2012）02－0095－05

2012－05－09 基金项目：国家自然科学基金资助项目（11161049）

＊通信作者：何延生（1962—），男，副教授，研究方向为微分方程及其应用．