新的矩阵特征值扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽274000）

新的矩阵特征值扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽274000）

通过引入正规性偏离度的概念，利用矩阵的分解和矩阵的计算技巧，得到了全新的任意矩阵特征值的扰动上界，所得结果推广了Wielandt－Hoffman定理．

矩阵；特征值；扰动上界

矩阵特征值的扰动理论是研究矩阵在某种特定的结构下，其特征值的扰动上界问题．目前，国内外许多学者对此进行了研究，例如：Hoffman和Wielandt［1］研究了原始矩阵A及其扰动矩阵B均为Hermite矩阵时的扰动上界；吕烔兴和宋永忠等［2－4］研究了A和B均为可对称化矩阵时的扰动上界，并且通过逐步减弱对矩阵A和B的限制，得到了A和B均为任意矩阵时的扰动界［5］．但上述结果应用起来比较繁琐，计算量较大，并且这些定理的取得都不是基于正规性偏离度的概念上．本文在引入矩阵正规性偏离度概念的基础上，利用矩阵的Schur三角分解和奇异值分解，得到了与正规性偏离度有关的任意矩阵特征值的绝对扰动上界，所得结果推广了Wielandt－Hoffman定理．

LBL组学员主要以面授课程为主，带教教师对EUS基本结构、操作手法、局部解剖、典型图例等内容进行统筹备课，按照难度循序渐进地设计课程进度，由浅入深地讲解EUS操作手法、EUS下胰腺及胆道正常结构及疾病典型图例(胰腺癌、胰腺囊肿、胰腺囊液腺瘤、胆道疾病等)，之后按照学员理解程度继续介绍EUS下治疗步骤。

攻击性较强的儿童往往缺乏解决交往问题的策略，不善于与他人建立良好的关系，不善于与他人进行交往。这就需要向儿童提供一些正常交往的策略，通过榜样的示范、解释和说明，帮助他们掌握减少人际冲突的策略，从而改善人际关系，减少攻击性行为。

1 相关定义和引理

定义1［6］（正规矩阵）若矩阵A∈Cn×n，满足AHA＝AAH，则A为正规矩阵；若满足AH＝A－1，则A为酉阵．

定义2［7］（Shur三角分解）设A∈Cn×n，则必存在酉阵U，使得UHAU＝T，其中T为上三角矩阵，λ1，λ2，…，λn为A的n个特征值，UH为矩阵U的共轭转置矩阵．当适当选取U时，可使T的对角线元素按任意指定顺序排列．T称为A的Shur上三角形式．

下面给出任意矩阵特征值的另1个Wielandt－Hoffman型扰动定理．

定义3［8］（正规性偏离度）设A∈Cn×n，ν是Cn×n上的任意一种范数．令三角形中的严格上三角矩阵｝，则称为A对于范数ν的正规性偏离度．

证明 由Schur三角分解定理知，对任意的A，B∈Cn×n存在酉阵P，Q使A＝PH（Λ1＋M1）P，B＝QH（Λ2＋M2）Q，其中Λ1＝diag（λ1，…，λn），Λ2＝diag（μ1，…，μn），M1和M2均为严格上三角阵．

特别地，A对于范数‖·‖F的正规性偏离度记为ΔF（A），对于范数的正规性偏离度记为为正规矩阵的充要条件是ΔF（A）＝0．

定义5［9］（矩阵条件数）设或2，或∞等）称为矩阵A的条件数．A的谱条件数（即取υ＝2）记为K（A）．

引理1［10］设A，B均为正规阵，X∈Cn×n为Hermite阵且X为正定阵，则

其中σ1（A）和σn（A）分别为矩阵A的最大和最小奇异值．

引理3［12］设A

2 主要结果及其证明

但是，如果认真审视这些关于工匠精神的研究，不难发现，必须细致分析“工匠精神”的内涵，精确把握工匠精神的要求，才有助于进一步阐发高职业教育如何培育“工匠精神”。“虽然目前学者对‘工匠精神’尚无标准权威的定义，但对其已达成基本一致的共识：工匠精神是对所从事的工作追求精益求精、勇于创新、一丝不苟的精神理念。”[4]143在笔者看来，工匠精神应该从如下四个层次做进一步的阐发：

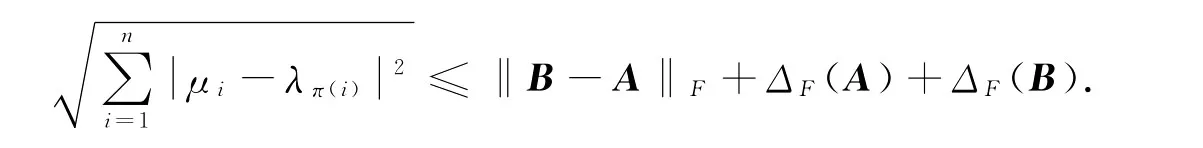
定义4［8］（矩阵的F－范数）设A∈Cm×n，令则称它为矩阵A的F－范数．

上式左边乘Q，右边乘PH，得Q（B－A）PH＝Λ2QPH＋M2QPH－QPHΛ1－QPHM1，即Λ2QPH－QPHΛ1＝Q（B－A）PH－M2QPH＋QPHM1．对QPH进行奇异值分解QPH＝UΣVH，Σ＝diag（σ1，…，σn），σ1≥ … ≥σn＞0，U和V为酉阵，Λ2UΣVH－UΣVHΛ1＝Q（B－A）PH－M2UΣVH＋UΣVHM1，将该式左边乘UH，右边乘V，得UHΛ2UΣ－ΣVHΛ1V＝UHQ（B－A）PHV－UHM2UΣ＋ΣVHM1V．令D＝UHΛ2U，C＝VHΛ1V，则D，C分别酉相似于Λ2，Λ1，故D，C均为正规阵，且D，C的特征值分别等于B，A的特征值，即DΣ－ΣC＝UHQ（B－A）PHV－UHM2UΣ＋ΣVHM1V．

19岁的杨梅是北京一所大学的大二学生。去年9月14日中午12点，刚回到家的杨梅接到一个电话，“我是电话局的，你家电话报修了，我马上到。”家里电话不好好的吗？杨梅正嘀咕呢，门铃响了。杨梅打开门把来人引到了电话机旁，准备去给师傅倒水。就在她转身的瞬间，她的右肩脖颈处挨了重重一拳。杨梅身子晃了晃，慢慢倒下。

引理2［11］设n阶方阵A＝（aij）的Schur三角分解为A＝UHTU，其中U为酉阵，T＝（tij）为上三角阵，记T＝Λ＋M，其中Λ＝diag（λi）为对角阵，M＝（mij）为严格上三角阵，则

证明 由Schur三角分解定理有A＝PH（Λ1＋M1）P，B＝QH（Λ2＋M2）Q，其中P，Q为酉阵，Λ1＝diag（λ1，…，λn），Λ2＝diag（μ1，…，μn），M1，M2均为严格上三角阵．

而此山此谷又可谓野花野谷王国。大别山特有的古杜鹃花群，春季在山坡上随处可见，宛若大片彩云，开得如痴如醉。野果有板栗、核桃、樱桃、猕猴桃、杏、枣、山楂、罗汉果、桑葚、松茸……野滋味与寻常水果不可同日而语。

这学期我们学了角的度量，在做练习题时我碰到了一道判断题：用放大镜去看一个角，这个角的度数会变大吗？我脑子里首先想到放大镜看东西会放大，那角应该也会放大。

由以上分析可知，热力型氮氧化合物和快速型氮氧化合物只占澳斯麦特炉烟气中的氮氧化合物的小部分，燃料型氮氧化合物是澳斯麦特炉烟气中的氮氧化合物的主要来源。

AX－XB＝PH（Λ1＋M1）PX－XQH（Λ2＋M2）Q＝PHΛ1PX＋PHM1PX－XQHΛ2Q－XQHM2Q，上式左边乘P，右边乘QH得Λ1PXQH＋M1PXQH－PXQHΛ2－PXQHM2＝P（AX－XB）QH．对PXQH进行奇异值分解PXQH＝UΣVH＝Udiag（σ1，…，σn）VH，σ1≥ … ≥σn＞0，U，V为酉阵，Λ1UΣVH＋M1UΣVH－UΣVHΛ2－UΣVHM2＝P（AX－XB）QH，上式左边乘UH，右边乘V有UHΛ1UΣ－ΣVHΛ2V＝UHP（AX－XB）QHV－UHM1UΣ＋ΣVHM2V．令D＝UHΛ1U，C＝VHΛ2V，则D，C分别酉相似于Λ1，Λ2，故D，C均为正规阵，且D，C的特征值分别等于A，B的特征值，即DΣ－ΣC＝UHP（AX－XB）QHV－UHM1UΣ＋ΣVHM2V．

注 取X为单位矩阵I，定理2变成定理1，该结果同样推广了Wielandt－Hoffman定理．

3 结束语

本文通过2个定理，给出了任意矩阵特征值新的绝对扰动上界，并且所得结论为Wielandt－Hoffman定理的进一步推广．文献［13］和［14］讨论了矩阵特征值的乘法扰动，能否得到含有正规性偏离度的乘法绝对扰动界，是我们将进一步研究的课题．

［1］ Hoffman A J，Wieandt H W．The variation of the spectrum of a normal matrix［J］．Duke Math J，1953，20（1）：37－39．

［2］ 吕烔兴．可对称化矩阵特征值的扰动［J］．南京航空航天大学学报，1994，26（3）：384－388．

［3］ 吕烔兴．可对称化矩阵特征值的扰动界［J］．高等学校计算数学学报，1994，16（2）：177－185．

［4］ 宋永忠．一类矩阵特征值的扰动［J］．纯粹数学与应用数学，1992，8（2）：106－108．

［5］ 吕烔兴．正规矩阵的任意扰动［J］．高等学校计算数学学报，2000，22（1）：85－89．

［6］ 蒋正新，施国梁．矩阵理论及其应用［M］．北京：北京航空学院出版社，1988：95－99．

［7］ 熊洪允，曾绍标，毛云英，等．应用数学基础［M］．天津：天津大学出版社，1994：72－74．

［8］ 孙继广．矩阵扰动分析［M］．北京：科学出版社，2001：10－226．

［9］ 易大义，陈道琦．数值分析引论［M］．浙江：浙江大学出版社，1998：280－285．

［10］ Bhatia R，Kittanch F，Li ren－cang．Some inequalities for commutators and application to spectral variatioⅡ［J］．Linear and Multilinear Algebra，1997，43：207－219．

［11］ 谈雪媛．关于方阵特征值扰动的两个注记［J］．南京师范大学学报：自然科学版，2002，25（4）：17－19．

［12］ Henrici P．Bounds for iterates，inverses，special variation and fields of values of non－normal matrices［J］．Numer Math，1962，4（1）：24－40．

［13］ Li R C．Relative perturbation theory：Ⅰeigenvalue and singular value variations［J］．SIAM Journal on Matrix Analysis and Applications，1998，19（4）：956－982．

［14］ Li R C．Relative perturbation theory：Ⅲmore bounds on eigenvalue variation［J］．Linear Algebra Applications，1996，266：337－345．

New upper bounds of perturbation for eigenvalues of arbitrary matrices

KONG Xiang－qiang
（Department of Mathematics，Heze University，Heze 274000，China）

Using the decomposition of matrix，we obtained the new upper bounds of perturbation for eigenvalues of arbitrary matrices which extend the Wielandt－Hoffman theorem．

matrix；eigenvalue；upper bound of perturbation

O241．6

A

1004－4353（2012）02－0118－04

2011－10－19 作者简介：孔祥强（1983—），男，助教，研究方向为应用数学．

山东省统计局重点课题项目（KT11048）；山东省教育科学“十二五”规划重点课题项目（2011GG049）