星形布局的不同构图的计算

张 军

（延边大学理学院 数学系，吉林 延吉133002）

星形布局的不同构图的计算

张 军

（延边大学理学院 数学系，吉林 延吉133002）

根据物理学中图态与数学中图的对应关系，从数学的角度构建了1个特殊的向量映射关系，应用图论、有限群对集合的作用、轨道及等价关系等将一类多部图按同构进行了分类，并给出了不同构图（态）数目的计算公式．

布局；不同构；不动点；有限群；轨道

自1935年Einstein等发表质疑量子力学完备性的论文以来，量子纠缠就一直成为量子力学中热点讨论的基本问题之一．研究［1］表明，很多经典方法所不能实现的量子信息方案都可以通过量子纠缠来辅助实现．近年来，一种特殊类型的多量子位纠缠态——图态引起了人们的关注，它是与数学中的图有关的一种特殊的纯多量子位纠缠态，图的结点就相当于物理系统，而图的边则表示2个不同物理系统之间的相互作用．图态的许多纠缠特性与相应的图有关，有些图态已成为量子计算和量子信息的重要资源，例如：团簇态是单向量子计算的有用资源，多量子位GHZ态是量子通讯的重要资源等［2］．本文根据图态与数学中图的对应关系，从数学的角度建立1个特殊的向量映射关系，应用图论、有限群对集合的作用、轨道及等价关系等将文献［3－9］等二部、三部图进行了推广，将文献［10］的串联式布局改成了星形布局，给出了一类多部图的不同构图（态）个数的计算公式．

1 向量映射与星形布局图

设有n＋1个集合，分别记为

定义1 设g＝（g01，g02，…，g0n），其中g0i为V0×Vi（i∈ 〈n〉）到｛0，1｝的映射，即对…，t0n）∈A，则可得V到A的1个映射g，称g＝（g01，g02，…，g0n）为向量映射．令V到A的向量映射集合为M＝｛g∶V→A｝＝AV．

定义2 设V＝V0×V1×…×Vn，对∀g∈M，称集合为广义边集．其中T表示分量都是0或1的n维向量，即T＝（t01，t02，…，t0n），t0i∈｛0，1｝，i∈〈n〉；αT表示在α的第1个分量和第i＋1个分量之间建有关系，记为t0i，i∈ 〈n〉．当t0i为0时，2个元素a0k与aik之间无边；当t0i为1时，2个元素a0k与aik之间有边．称（V ，Eg）为以V为结点集，以Eg为边集，以V0为中心的n＋1部星形图，记为

令n＋1部星形图Gg的集合为所

定义3 设Gg1＝ （V，Eg1），Gg2＝ （V，Eg2）∈X．若存在双射σ∶V→V满足，则称Gg1与Gg2为同构的n＋1部星形图，

定义4 设Gg∈X，称集合部星形图Gg的等价类；集合中的任意元素（n＋1部星形图）称为Q（Gg）的代表元，且记n＋1部星形图的等价类的集合为Qe＝

2 Burnside引理的应用

设有限群S＝Sm0×Sm1× … ×Smn，其中Smj（0≤j≤n）均为对称群．∀σ＝（σ0，σ1，…，σn）定义σ对Gg的作用：σ（Gg）表示在σ（α）的第1个分量和第i＋1个分量之间建有关系当t0i为0时，2个元素之间无边；当t0i为1时，2个元素之间有边．称（V ，Eg）为以V为结点集，以Eg为边集，以V0为中心的n＋1部星形图，记为

令n＋1部星形图Gg的集合为所

定义3 设Gg1＝ （V，Eg1），Gg2＝ （V，Eg2）∈X．若存在双射σ∶V→V满足，则称Gg1与Gg2为同构的n＋1部星形图，

定义4 设Gg∈X，称集合部星形图Gg的等价类；集合中的任意元素（n＋1部星形图）称为Q（Gg）的代表元，且记n＋1部星形图的等价类的集合为Qe＝

2 Burnside引理的应用

设有限群S＝Sm0×Sm1× … ×Smn，其中Smj（0≤j≤n）均为对称群．∀σ＝（σ0，σ1，…，σn）定义σ对Gg的作用：σ（Gg）表示在σ（α）的第1个分量和第i＋1个分量之间建有关系当t0i为0时，2个元素之间无边；当t0i为1时，2个元素之间有边．因此，有限群作用n＋1部星形图Gg∈X的轨道为

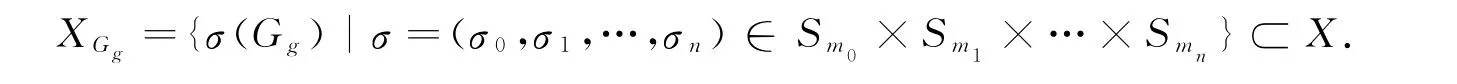
3 结论与计算

由对称群Smj（0≤j≤n）的元素性质可知，当σj∈Smj时，∃λj1，λj2，…，λjmj∈｛0，1，2，…，mj｝，

定义5 设Smj（0≤j≤n）均为对称群型置换．令）型元素．

其中（＊，＊）表示2个数的最大公因数．

由式（1）和式（2）可得有限群S＝Sm0×Sm1×…×Smn作用于n＋1部星形图集X上的不同轨道数N为

例题1 设4个集合分别为V0＝｛a01，a02｝，V1＝｛a11，a12，a13｝，V2＝｛a21，a22｝，V3＝｛a31｝，求以V0为中心的不同构4部星形图的个数．

解 设V＝V0×V1×V2×V3，A＝｛（t01，t02，t03）｜t0i∈ ｛0，1｝，i∈ 〈3〉｝，向量映射g＝（g01，g02，g03），即对任意的α＝（a0k0，a1k1，a2k2，a3k3）∈V，k0∈ 〈2〉，k1∈ 〈3〉，k2∈ 〈2〉，k3∈ 〈1〉，有g（α）＝（g01（α），g02（α），g03（α））∶＝（g01（a0k0，a1k1），g02（a0k0，a2k2），g03（a0k0，a3k3））＝（t01，t02，t03）∈A，其中t0i∈ ｛0，1｝，i∈ 〈3〉．记向量映射集合M＝｛g∶V→A｝＝AV，4部星形图集合X＝｛Gg｜g∈M｝．现计算与V对应的有限群S＝S2×S3×S2×S1作用于4部星形图集X上的轨道个数N．因有限群S＝S2×S3×S2×S1的所有可能的不同型元素为（12，13，12，11），（12，13，21，11），（12，1121，12，11），（12，1121，21，11），（12，31，12，11），（12，31，21，11），（21，13，12，11），（21，13，21，11），（21，1121，12，11），（21，1121，21，11），（21，31，12，11），（21，31，21，11），利用公式（3）计算S作用在X上的轨道个数，则所求不同构4部星形图的个数为

［1］ 许金时，李传锋，张永生，等．量子关联［J］．物理，2010，39（11）：729－730．

［2］ 计新．多量子位纠缠态的制备［D］．哈尔滨：哈尔滨工业大学，2011．

［3］ 张军，金明爱，冯恩民．换热网络布局问题的不动点集性质及计算［J］．运筹与管理，2001，10（3）：89－92．

［4］ 廉晓龙，魏连鑫，张军，等．三部图中无向不同构图的计算［J］．上海理工大学学报，2010，32（6）：602－604．

［5］ 冯恩民，张军，王锡禄．换热网络综合问题中的布局优化［C］//中国运筹学会第六届学术交流会论文集．香港：Global－Link出版社，2000：542－547．

［6］ 廉晓龙，张军．换热网络布局问题的不同构图的计算［J］．延边大学学报：自然科学版，2009，35（4）：309－311．

［7］ 张军．换热网络布局问题的改进及计算［J］．延边大学学报：自然科学版，2006，32（4）：40－43．

［8］ 廉晓龙，张军．一类网络布局优化问题的不同构图的计算［J］．延边大学学报：自然科学版，2008，34（3）：177－178．

［9］ 孙吉荣，廉晓龙，丁巍巍，等．一类三部图中不同构图的计算［J］．延边大学学报：自然科学版，2009，35（2）：109－111．

［10］ 方艳蓝，金美英，廉晓龙，等．n个集合串联式布局的不同构图的计算［J］．延边大学学报：自然科学版，2010，36（1）：34－37．

［11］ 胡冠章．应用近世代数［M］．2版．北京：清华大学出版社，1999：108－109．

The calculation of the graph of non－isomorphism in starlike layouts

ZHANG Jun
（Department of Mathematics，College of Science，Yanbian University，Yanji 133002，China）

Based on the corresponding relation between the physical graph state and the mathematical graph，we constructe a particular vector mapping from the view of mathematics．And by applying graph theory，finite group acting on sets，orbit and equivalent relation and so on，a multipartite graphs are classified according to the isomorphism．Finally，a computational formula is given for non－isomorphic graph（state）．

layout；non－isomorphism；fixed points；finite group；orbit

O157．5

A

1004－4353（2012）02－0115－03

2012－06－02

张军（1957—），男，教授，研究方向为布局优化．