若干倍图的(2,1)-全标号
刘秀丽
(菏泽学院 数学系,山东 菏泽274015)
若干倍图的(2,1)-全标号
刘秀丽
(菏泽学院 数学系,山东 菏泽274015)
研究了与频道分配有关的一种(p,1)-全标号染色问题.根据倍图的构造特征,利用穷染法,给出了一种标号方法,得到了路、圈、星、扇的倍图的(2,1)-全标号数.(p,1)-全标号是对图的全染色的一种推广.
染色;(p,1)-全标号;(p,1)-全标号数;倍图
随着图的染色问题在现实中的广泛应用,它逐渐成为众多学者研究的重要领域之一.图的着色问题是图论中的重要研究分支,有很强的理论意义和实际意义.近年来,许多新的染色问题被提出,这些染色问题在频率分配中有很强的应用,如泛宽度染色、L(p,1)-标号[1-3]等.特别地,Whittlesey等人在文献[4]中研究了G的剖分图的L(2,1)-标号,G的剖分图S1(G)是由图G在每条边上插入1个点所得到的图.S1(G)的L(p,1)-标号对应于G的(p,1)-全标号.
图G为简单连通图,用V(G)、E(G)和Δ(G)分别表示图G的顶点集、边集和顶点的最大度.本文所讨论的图均为简单、有限图.
1 预备知识
定义1[5]设p是1个非负整数,图G的1个k-(p,1)-全标号是1个映射f∶V(G)∪E(G)→{0,1,…,k},使得:
当p=1时,图G的(p,1)-全标号对应于图G的全染色,因此,图的(p,1)-全标号也是对图的全染色的一种推广.本文主要讨论了若干倍图的(2,1)-全标号.
定义2[6]对简单图G,其顶点集为V(G)={u1,u2,…,un},图G′为G的拷贝,其顶点集V(G′)={v1,v2,…,vn},则称D(G)为G的倍图,其中:
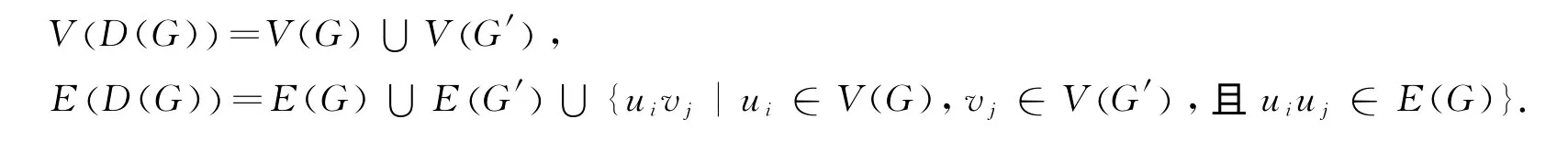
引理1[5]对任意图G,有
引理2[7]若图G满足,映射f表示图G的1个标号集是{0,1,2,…,Δ(G)+1}的(2,1)-全标号,那么对图G的每个最大度点v,有f(v)=0或f(v)=Δ(G)+1.
引理3[5]若G是正则的,则λpT(G)≥Δ+p.
文中未加说明的记号和术语参见文献[8-9].
2 主要结果及证明
定理1 设Pn是阶为nn≥3的路,则
证明 1)n=3.由图D(Pn)的定义知由引理1有
2)n=4.由图D(Pn)的定义知,.由引理1有
综上,当n=4时,有λ2T(D(P4))=5.
3)n≥5.由图D(Pn)的定义知由引理1有

易证映射f是D(Pn)的1个正常的(2,1)-全标号,所以
定理2 设Cn是阶为n(n≥3)的圈,则
证明 由图D(Cn)的定义知且为正则图.由引理3有
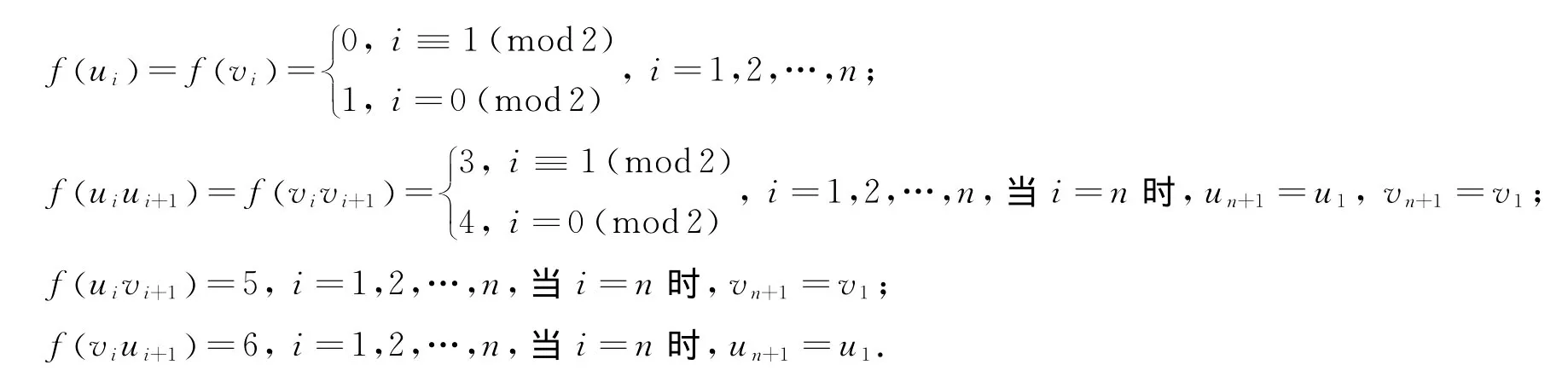
易证映射f是D(Cn)的1个正常的(2,1)-全标号,所以

易证映射f是D(Cn)的1个正常的(2,1)-全标号,所以
定理3 设Sn是阶为n+1(n≥2)的星,则
当n≥3时,由图D(Sn)的定义知由引理1有
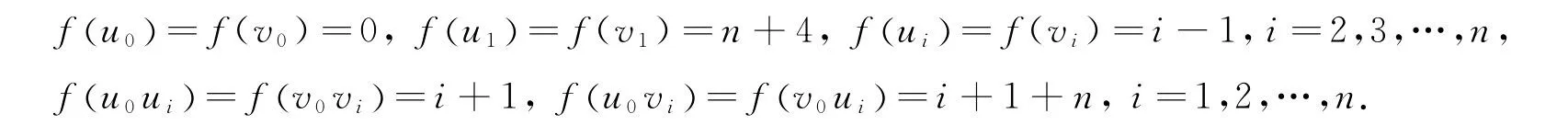
易证映射f是图D(Sn)的1个正常的(2,1)-全标号,所以
定理4 设Fn是阶为
2)当n=3时,由图D(Fn)的定义知.由引理1有

3)当n≥4时,由图D(Fn)的定义知,Δ(D (Fn))=2n.由引理1有=2n+1.
下证λ2T(D(Fn))≤2n+1.构造1个映射令

易证映射f是图D(Fn)的1个正常的(2,1)-全标号,所以λ2T(D(Fn))≤2n+1.
综上,当n≥4时,有λ2T(D(Fn))=2n+1.
[1] Griggs J R,Yeh R K.Labeling graphs with a condition at distance two[J].SIAM J Discrete Math,1992,5(4):586-595.
[2] Georges J P,Mauro D W,Stein M I.Labeling products of complete graphs with a condition at distance two[J].SIAM J Discrete Math,2001,14(1):28-35.
[3] Georges J P,Mauro D W,Whittles M A.Relating path covering to vertex labeling with a condition at distance two[J].Discrete Math,1994,135(1/3):103-111.
[4] Whittles M A,Georges J P,Mauro D W.On theλ-number of Qnand related graphs[J].SIAM J Discrete Math,1995,8(4):499-506.
[5] Havet F,Yu M L.(p,1)-Total labeling of graphs[J].Discrete Math,2008,308(4):496-513.
[6] 王志文,杨随义,文飞.关于若干倍图的关联邻点可区别全染色[J].内蒙古师范大学学报:自然科学版,2009,38(6):643-646.
[7] Chen Dong,Wang Wei-fan.(2,1)-Total labeling of outer planar graphs[J].Discrete Applied Mathematics,2007,155(18):2585-2593.
[8] Bollobas B.Modern Graph Theory[M].New York:Springer-Verlag,1998:147-189.
[9] Bondy J A,Murty U S R.Graph Theory with Applications[M].London:Macmillan Press Ltd,1976:128-196.
The(2,1)-total labelling of some double graphs
LIU Xiu-li
(Department of Mathematics,Heze University,Heze 274015,China)
We study a coloring problem—(2,1)-total labeling of some graphs,which is related to frequency assignment.By using the eternal coloring method,we give a new labeling method according to the feature of the double graphs of path,circle,star,fan and obtain the(2,1)-total numbers of these graphs.And the(p,1)-total labeling of graphs extends the total coloring of graphs.
coloring;(p,1)-total labelling;(p,1)-total number;double graph
O157.5
A
1004-4353(2012)02-0104-04
2012-06-03
刘秀丽(1977—),女,讲师,研究方向为图论与组合优化.

