预应力曲杆的Cosserat动力学模型

曹登庆，宋敉淘

（哈尔滨工业大学航天学院，150001 哈尔滨）

预应力曲杆的Cosserat动力学模型

曹登庆，宋敉淘

（哈尔滨工业大学航天学院，150001 哈尔滨）

为了更方便地使用Cosserat杆模型对各种细长结构进行动力学建模，在该杆模型的框架下通过引入描述固连在杆横截面随其一起运动的初始变形、初始横截面转动以及横截面间的初始接触力和力矩等变量，建立了考虑预应力的细长曲杆的Cosserat动力学模型.在得到的模型的框架下，基于相应的物理假设，从数学演绎的角度推导了桥梁建设中广泛应用的具有初始垂度的拉索以及圆拱梁的动力学方程，结果与文献中采用其他方法得到的相应的动力学方程一致.由于Cosserat理论采用了精确的几何构形，这里导出的细长预应力曲杆动力学模型不仅保留了所有的几何非线性特征，而且具有很好的普适性，通过它可以容易地导出实际工程问题中细长结构的非线性动力学模型.

Cosserat杆模型;预应力曲杆;具有初始垂度的拉索;圆拱梁

18世纪的Bernoulli和Euler认为梁之所以能抗弯是梁在运动过程中轴向伸缩的结果，且梁横截面受到的弯矩正比于梁轴线的曲率.Euler-Bernoulli梁模型用梁轴线的挠度描述梁的运动，梁横截面的转动用挠度对空间坐标的导数来描述.Coulomb于1776年首次将力和力矩的平衡方程用于对梁微元进行力学分析，建立了较Euler-Bernoulli梁更为精确的动力学方程，并开始考虑梁承受扭矩的情况［1］.Kirchhoff于1859年计算了杆单元的应变，从能量的角度得到了杆的动力学方程，并提出了基于 Kirchhoff动力学比拟［2－3］的 Kirchhoff弹性杆模型.该模型忽略杆轴线的伸缩变形和横截面的剪切变形，并将杆横截面视为刚体，以描述杆轴线的3个线位移参数以及描述各横截面的3个姿态参数为未知变量建立杆的动力学方程.Rayleigh于1877年引入梁横截面惯性矩的影响，考虑轴向和横向振动对梁进行建模，并指出在高频振动时该修正是很必要的［1］.Timoshen-ko［4－5］引入梁横截面间剪切力的影响对梁进行建模，并指出 Euler-Bernoulli梁和 Rayleigh梁为Timoshenko梁的两种特殊情况.更加精确的杆的动力学模型的问世随着工程设计和分析的需要而显得越来越必要和迫切.

近年来，基于Cosserat兄弟和其他人的早期工作，形成了关于细长杆的Cosserat介质理论.Antman［6］在他的著作中运用该理论的基本思想建立了柔性杆和薄壳的Cosserat模型.Tucker和Wang［7］和 Cao 等［8－9］进一步完善了 Cosserat杆理论，并分别应用于对钻柱的非线性动力学研究和MEMS中复杂结构三维非线性动力学模拟.Burton和Tucker［10］回顾了Cosserat杆模型的发展以及它近年来在各个领域中的应用.国内学者在Cosserat杆模型上也做了很多重要的工作.刘延柱等［11－12］从更偏重于力学分析的角度得到了任意初始构形圆截面Cosserat杆的动力学方程，在其框架下推导了Rayleigh梁、Kirchhoff杆、以及Timoshenko梁的动力学方程，并对基于精确的Cosserat杆模型螺旋杆进行了稳定性分析.Cosserat杆模型在Kirchhoff杆模型的基础上考虑了杆轴向的伸缩变形以及横截面间剪切力引起的横截面的转动，由于所作的假设更少，Cosserat杆模型较以往的杆模型都更为精确.

鉴于Antman所建立的 Cosserat杆模型［6］几何形式的直观性，本文的工作将在其框架下进行.本质上Cosserat杆模型适用于对具有任何初始构形和预应力的杆进行建模，但为了讨论的方便，以往文献中给出Cosserat杆动力学方程的同时，在Cosserat杆的本构关系中实际上都只将杆的由预应力引起的初始变形用1个抽象的符号表示，或者直接只考虑无预应力直杆(Non-Prestressed Straight Rod，NPSR)的情况［7－9］，而且在 Cosserat杆的动力学方程中，他们并没有对初始量和动力学意义上的量进行区分.如何在Cosserat杆动力学方程以及其本构关系中加入杆的初始构形和预应力项以描述具有预应力的曲杆(Prestressed Curved Rod，PCR)的动力学行为是关键.本文的目的便是依据文献中NPSR的Cosserat模型的基本思想，用Cosserat杆模型对PCR进行建模，并称得到的模型为PCR的Cosserat动力学模型.在该模型的框架下，再根据具体的假定，便可以很明确地从数学演绎的角度推导各种特殊情况下的一维细长结构的动力学模型.本文中，矢量用小写斜体黑体字母表示，如u，v和w;张量用大写斜体黑体字母表示，如K，I和J;重复下标为哑指标，表示采用爱因斯坦求和约定;运算符⊗为两张量间的张量积运算.

1 NPSR的Cosserat模型

考虑一根细长杆，在初始时刻t0时各横截面质心组成的曲线(质心线)上定义拉格朗日弧坐标s，s∈［0，L0］，L0为杆的初始长度.如图1所示，假设运动过程中t时刻杆的质心线为r(s，t)，分别以r(s，t)上的各点为原点定义局部的右手笛卡尔直角坐标系 s ∈ ［0，L0］|→{d1(s，t)，d2(s，t)，d3(s，t)}，并将坐标系固定在相应位置处杆的横截面上.将d1(s，t)垂直于相应位置处杆的横截面，将d2(s，t)和d3(s，t)置于相应位置处杆横截面内.忽略杆运动和变形过程中密度和横截面面积的变化，于是Cosserat杆模型的动力学方程可以由牛顿第二定律得到:

式中:ρ(s)为杆的密度;A(s)为杆的横截面面积;n(s，t)和m(s，t)分别为杆横截面间接触力和接触力矩;f(s，t)和l(s，t)分别为外力密度和外力矩密度(可以包括重力，阻尼力，电磁力，气动力等);I(s，t)为截面的惯性矩张量.

图1 Cosserat杆模型

由于Cosserat杆模型考虑了剪切力引起的杆横截面的转动，于是r'(s，t)不再始终垂直于相应位置处的横截面，令

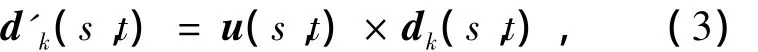
式(3)和(4)分别意味着(参见文献［6－9］)

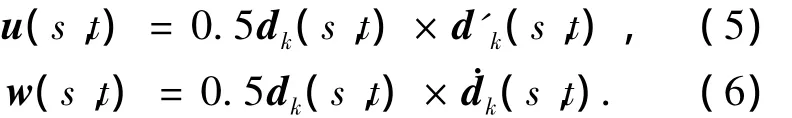
于是，Cosserat杆的本构关系可以表示为如下形式:

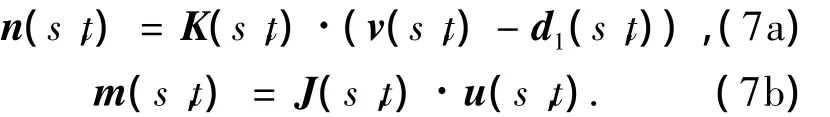
式(7)中的张量 K(s，t)和 J(s，t)以及式(1b)中的张量I(s，t)的分量形式分别为

式中:E(s)为杆的弹性模量;G(s)为杆的剪切模量;dA=dξdη，η和ξ分别为坐标系基矢量d2(s，t)和d3(s，t)对应坐标轴的坐标;Ψ(ξ，η)为横截面的翘曲函数，由圣维南原理知其对于所有横截面都相同［13］;κ(s)为 Timoshenko剪切系数，现有不同的理论对其进行物理意义上的解释，Shames和Dym［14］系统探讨过这个问题，但不论哪种解释，κ(s)的值都取决于横截面的形状.张量I(s，t)和J(s，t)可以通过选择 d2(s，t)和 d3(s，t)的方向达到对角化，以使得它们的形式变得更为简洁.

下面阐述式(7)中NPSR的Cosserat模型本构关系背后的力学依据.式(7a)中出现的d1(s，t)表示t0时刻杆的质心线没有剪切变形，只有沿着杆相应处横截面法向的变形.由于采用了杆初始构形上的弧坐标，于是初始时刻质心线对弧坐标的微分总是为d.杆初始构形上任意一微元ds便可以用ds d作为其长度和方向的度量，它随着杆的整体运动而运动，作为微元的初始状态始终垂直于相应位置处的横截面，于是变为ds d1(s，t).同时，变形后的微元为v(s，t)ds.于是微元的正应变(沿d1(s，t)的方向)以及剪切应变(分别沿着d2(s，t)和 d3(s，t)的方向)分别为

在 d1(s，t)，d2(s，t)和d3(s，t)上的投影.至此，便不难得到式(7a).式(7b)表示横截面间的接触力矩由横截面间相对转角来度量，对其分析可类似于对式(7a)所作的分析那样，通过定义随着杆整体运动的杆横截面的初始转角而实现.由于在前面定义的初始时刻局部坐标系间没有相对转角，于是初始时刻横截面间无相对转角.由上面分析可见，本构关系(7)的获得，关键在于定义随着杆横截面一起运动的各种初始量，这给PCR的本构关系的建立及分析预应力对动力学方程的影响提供了思路.

2 PCR的Cosserat模型

假如细长杆为PCR，即杆的横截面与横截面间接触力n(s，t)和接触力矩m(s，t)在t=t0时不为零(即 n0(s)=n(s，t0)≠ 0，m0(s)=m(s，t0)≠0)，则在静平衡位置处杆在预应力和初始外力f0=f(s，t0)和初始外力矩l0=l(s，t0)作用下保持平衡，由牛顿第二定律得

其中r0(s)=r(s，t0)为静平衡位置时杆的质心线.杆质心线上各质点的线位移分为静位移r0(s)和动位移rd(s，t)两部分，即

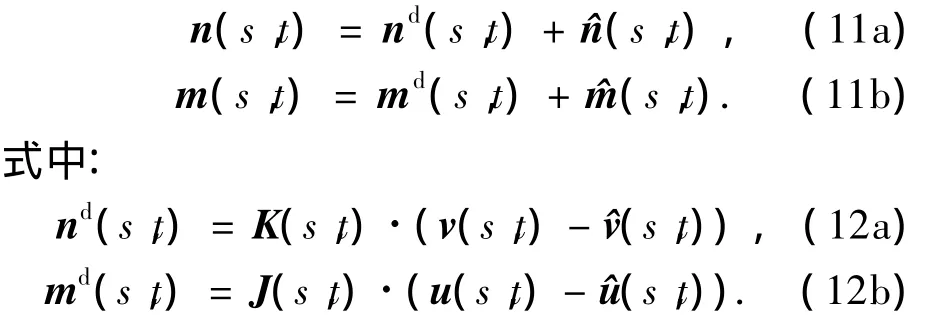
式(11)和(12)中

在初始局部坐标系下的分量.ξij(s，t)=d(s)·dj(s，t).由第1节的内容知道u(s)由d(s)的定义决定.为了保证类似于式(5)的定义有意义，应将d(s)取为s个连续的单位矢量函数.曲杆无法做到像直杆那样将d(s)独立于s.不考虑杆运动过程中产生裂缝的情况，d(s)取为垂直于相应位置处的横截面能保证d(s)连续.同时，取d(s)和d(s)为任意的连续单位矢量函数都不会影响到最后的结果.因为d(s)的选取影响着u(s)的同时，也影响着 di(s，t)，进而导致 u(s，t)－(s，t)的值不依赖于d(s)的选取.将外力(外力矩)分为初始力(初始力矩)和动态力(动态力矩)两部分，即

将式(10)－(16)代入式(1)中，并将得到的两方程分别减去式(9)中的两个方程得到PCR的Cosserat模型的动力学方程为

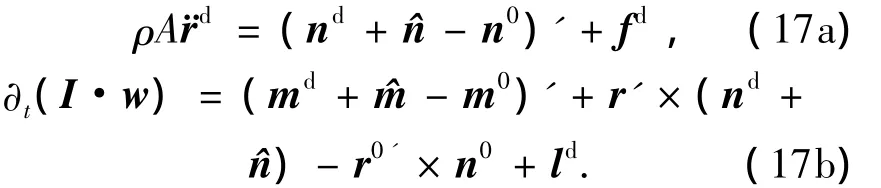
当n0、m0和r0为零时，式(17)退化为式(1)的形式.

值得注意的是，拉索可以视为杆忽略弯扭刚度以及横截面间剪切刚度的特殊情况，于是具有初始垂度的拉索的动力学方程可以由方程(17a)来描述，而且此时张量K需要退化成如下形式:

另外需要注意的是，前面的推导是在假定曲杆的横截面、初始质心线、横截面间初始接触力以及初始接触力矩为已知的前提下进行的.实际在一般情况下，对于曲杆，特别是具有预应力的曲杆，如何选择杆横截面并不是一件容易的事情.同时，求解杆的预应力也非易事.不过，这并非我们所关心的主要问题.而且，对于很多特殊情况，确定杆的上述初始量并不困难，作为例子我们将在第3节中采用本节建立的PCR的Cosserat模型推导具有初始垂度的空间拉索以及圆拱梁的动力学方程的过程中可以看到.

3 两类特殊PCR的动力学建模

3.1 具有初始垂度的空间拉索动力学建模

如图2所示，在全局右手笛卡尔直角坐标系{o;e1，e2，e3}下，具有初始垂度的拉索运动过程中的形状为

其中 W1(s，t)，W2(s，t)和 W3(s，t)分别为拉索各质点在e1，e2和e3方向的线位移.

图2 具有初始垂度的空间拉索的运动示意图

由于不考虑拉索横截面间剪切力的影响，于是d1(s，t)沿着拉索的切线方向，即

将式(18)代入式(2)得

全局坐标系下张量K写成矩阵形式为

将式(19)－(21)代入式(12a)，并根据式(13)得

另一方面拉索的动应变e(s，t)为

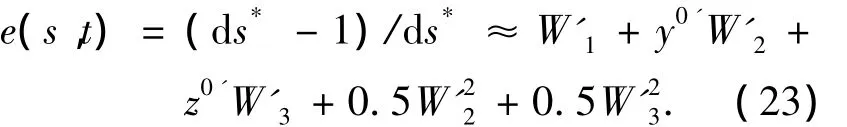
于是由式(22)和(23)得

若拉索初始张力为H，则

将式(28)进行泰勒级数展开，忽略高于一阶的小量并整理得

将阻尼从外力中分离出来，即

其中c为阻尼系数.将式(18)，(29)和(30)代入式(17a)中得到拉索动力学方程为

3.2 圆拱梁的动力学建模

如图3所示，初始时刻圆拱梁圆心为o.如果不考虑圆拱梁的预应力，则可以通过如下方式选取圆拱梁的横截面:通过o点，取垂直于圆拱梁所在平面的平面，并让它与圆拱梁相截，则截出的圆拱梁的截面即可选为圆拱梁的横截面.

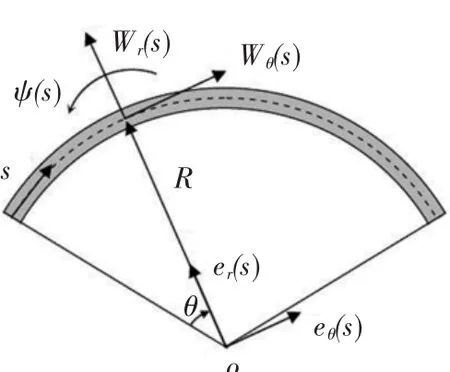
图3 圆拱梁的初始构形及坐标系的定义

在圆拱梁初始构形上对质心线每个质点s建立 右 手 笛 卡 尔 直 角 坐 标 系 {o;eθ(s)，er(s)，ez(s)}，其中eθ(s)沿着质心线在s处的切线方向并且指向s增加的方向，er(s)从o指向s，ez(s)=eθ(s)×er(s).可见，ez(s)实际上不随s而变化.圆拱梁初始时刻质心线为

圆拱梁在运动过程中质心线的形状为

其中Wθ(s，t)和 Wr(s，t)分别为 t时刻质点 s在eθ(s)和er(s)方向的线位移.取

记圆拱梁横截面相较于初始构形转过的角度为ψ(s，t)，并以逆时针转动为正，于是

将式(32)和(33)分别代入式(2)，将式(34)代入式(6)，将式(35)分别代入式(5)和(6)，并根据式(13)－(15)得

由于不考虑圆拱梁的预应力，即

二维情况下，张量 K在坐标系{o;eθ(s)，er(s)，ez(s)}中的分量形式为

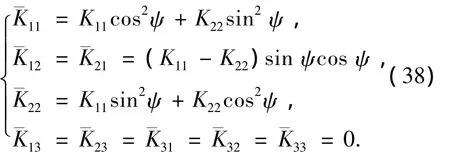
张量J和 I在坐标系{o;eθ(s)，er(s)，ez(s)}中的分量形式分别为

同样地将阻尼从外力中分离出来，并将式(33)，(36)－(39)代入式(17)中得到圆拱梁的动力学方程为

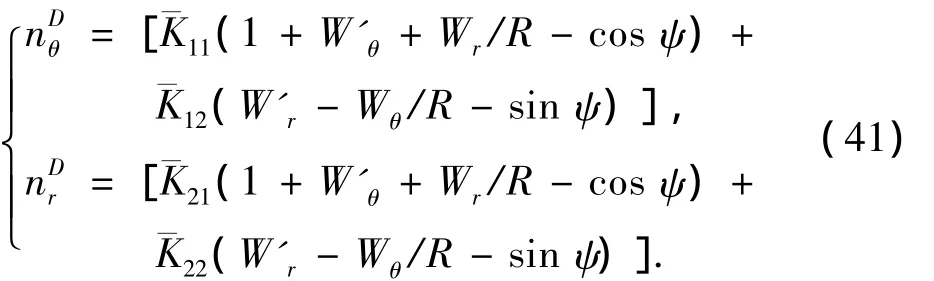
若圆拱梁为小变形，则可以用式(40)的线性化形式来描述圆拱梁的运动，此时式(41)退化为

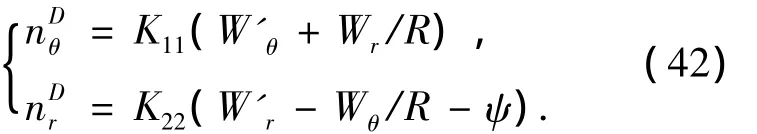
将式(42)和(8)代入式(40)，并忽略非线性项得

若忽略阻尼和外力，式(43)和文献［16］中用广义Hamilton原理得到的圆拱梁的线性动力学方程一致.

4 结论

1)建立了初始局部坐标系下杆各初始量(质心线的初始变形，横截面的初始转角，横截面间的初始接触力和接触力矩)与运动过程中它们反映在PCR的Cosserat动力学方程和本构关系式中的相应的初始变量的具体关系.

2)将初始变量耦合进Cosserat杆动力学模型及其本构关系中建立了PCR的Cosserat动力学模型及其本构关系.

3)作为特例，桥梁中广泛使用的具有初始垂度的空间拉索以及圆拱梁的动力学方程在PCR的Cosserat动力学模型的框架下作了推导.其过程体现了Cosserat杆模型包容性强以及数学推导的透明性和一贯性，简化了繁杂的物理和力学层面上的分析过程.PCR的Cosserat动力学模型的建立使得各种特殊的一维细长结构的动力学建模变成了一个很纯粹的数学推导过程，极大地方便了使用Cosserat杆模型对各种特殊的一维细长结构的建模.

［1］ARAFAT H N.Nonlinear response of cantilever beams［D］.Blacksburg，Virginia:Virginia Polytechnic Institute and State University，1999:17－18.

［2］LOVE A E H.A treatise on the mathematical theory of elasticity［M］.New York:Dover，1944:399 －400.

［3］刘延柱.弹性细杆的非线性力学［M］.北京:清华大学出版社，2006:14－18.

［4］TIMOSHENKO S P.On the correction for shear of the differential equation for transverse vibrations of prismatic bars［J］.Philosophical Magazine，1921，41(1):744 －747.

［5］TIMOSHENKO S P.On the transverse vibrations of bars of uniform cross section［J］.Philosophical Magazine，1922，43(1):125－131.

［6］ANTMAN S S.Nonlinear problems in elasticity［M］.New York:Springer-Verlag，1995:13－359.

［7］TUCKER R W，WANG C.Torsional vibration control and Cosserat dynamics of a drill-rig assembly［J］.Meccanica，2003，38(1):143－159.

［8］CAO Dengqing，LIU Dongsheng，WANG C H－T.Nonlinear dynamic modelling for MEMS components via the Cosserat rod element approach［J］.Journal of Micromechanics and Microengineering，2005，15(6):1334 －1343.

［9］CAO Dengqing，TUCKER R W.Nonlinear dynamics of elastic rods using the Cosserat theory:modelling and simulation［J］.International Journal of Solids and Structures，2008，45(2):460 －477.

［10］BURTON D A，TUCKER R W.Practical applications of simple Cosserat methods［C］//Mechanics of Generalized Continua.In:Advances in Mechanics and Mathematics.Berlin:Springer，2010，21:87 －98.

［11］LIU Yan-zhu.On dynamics of elastic rod based on exact Cosserat model［J］.Chinese Physics B，2009，18(1):1 －8.

［12］刘延柱，薛纭.基于精确Cosserat模型的螺旋杆稳定性分析［J］.应用数学和力学，2011，32(5):570－578.

［13］TIMOSHENKO S P，GOODIER J N.Theory of elasticity［M］.New York:McGraw-Hill，1951:275 －313.

［14］SHAMES I H，DYM C L.Energy and finite element methods in structural mechanics［M］.Chaman Offset，Delhi，India:New Age International Publishers，1991:197 －203.

［15］SOFI A，MUSCOLINO G.Dynamic analysis of suspended cables carrying moving oscillators［J］.International Journal of Solids and Structures，2007，44(21):6725 －6743.

［16］JAVID F，ESMAILZADEH E，YOUNESIAN D.An investigation into the vehicle-curved bridge dynamic interaction［J］.International Journal of Automotive Engineering，2011，1(3):235－243.

Dynamic modeling of pre-stressed curved Cosserat rods

CAO Deng-qing，SONG Mi-tao

(School of Astronautics，Harbin Institute of Technology，150001 Harbin，China)

To dynamically model slender structures conveniently by Cosserat rod theory，the dynamic equations for pre-stressed curved Cosserat rods are established within the framework of this rod theory by defining variables to describe their initial configurations，their pre-stresses and their initial deformations，which move along with their cross sections.Based on their corresponding specific assumptions，the dynamic equations for a cable with initial sag and a circular arch beam，which have wide applications in bridge structures，are explored within the framework of pre-stressed curved Cosserat rods，respectively.The results are in agreement with their corresponding equations obtained by other methods in references.Since the Cosserat theory is geometrically exact，the dynamic equations for pre-stressed curved Cosserat rods derived here are not only retaining all geometric nonlinear characteristics but also of universality，which can be effectively and efficiently exploited to nonlinear dynamically model for slender structures in practical engineering situations.

Cosserat rod;pre-stressed curved rod;cable with initial sag;circular arch beam

O326;O341

A

0367－6234(2012)11－0001－06

2012－02－12.

国家自然科学基金资助项目(10772056).

曹登庆(1958—)，男，教授，博士生导师.

曹登庆，dqcao@hit.edu.cn.

(编辑 张 宏)