升力式再入飞行器覆盖范围计算分析

傅 瑜，杨卫丽，崔乃刚

（1.哈尔滨工业大学航天学院，150001 哈尔滨;2.国防科技信息中心，100142 北京）

升力式再入飞行器覆盖范围计算分析

傅 瑜1，杨卫丽2，崔乃刚1

（1.哈尔滨工业大学航天学院，150001 哈尔滨;2.国防科技信息中心，100142 北京）

将升力式再入飞行器的覆盖范围生成问题转化成满足再入约束条件下的最大纵程、最小纵程、最大横程以及一定纵程下最大横程的轨迹优化问题，采用序列梯度－修复算法来解这一系列的轨迹优化问题，最后进行了仿真分析.仿真结果表明:本文采用的方法合理可行，升力式再入飞行器的覆盖范围为一个左右不对称的扇形区域.

升力式再入飞行器;覆盖范围;轨迹优化;序列梯度－修复算法

升力式再入飞行器的覆盖范围定义了飞行器潜在的可达区域，可为飞行器在正常和异常飞行情况下的任务规划提供选择依据，可以帮助飞行器在正常的再入飞行和偶然突发事件中变更或选择潜在的着陆位置.因此，升力式再入飞行器当前时刻的覆盖范围，即一系列的可行着陆区域，是其安全飞行的重要保证.特别是全球到达的升力式再入飞行器，覆盖范围的分析更有着非常重要的意义.

目前国外相关文献主要有两类方法来求解该问题.一类是利用平衡滑翔条件简化运动方程，降低该问题的复杂性进行逼近.文献［1］通过坐标变换，在不考虑路径约束的情况下，将该问题转换成一系列简单的纵程不定情况下的最大横程问题，并通过参数搜索来求解.文献［2］采用拟平衡滑翔条件，将覆盖范围生成问题等效为解决一系列简单的运动虚拟目标的逼近问题.然后，采用近似最优控制律，该逼近问题又转化成1个一维求根问题.同时，根据倾侧角－速度再入走廊，加入了一般的不等式约束，快速、可靠地获得了考虑约束条件下的任意再入初始条件的高精度覆盖范围.第二类是基于航天飞机再入制导方法［3］的逼近.其原理是认为升力式再入飞行器所能覆盖的射程与其阻力加速度的大小成反比，且其覆盖范围可由多边形进行近似.在由不等式定义的再入飞行走廊内，先规划出最大射程和最小射程的阻力加速度剖面.覆盖范围的远边界由最大射程的阻力加速度剖面决定，近边界由最小射程的阻力加速度剖面决定，并用直线近似.对于其它边界，其阻力加速度剖面由最大阻力加速度剖面和最小阻力加速度剖面线性插值得到，然后采用由跟踪制导律决定的不变号的倾侧角进行飞行仿真并最终获得再入飞行器的覆盖范围.文献［4］给出了该类方法更为详细的细节，航天飞机的事故飞行管理也是基于上述方法［5］.而国内学者主要直接通过优化的方法来进行求解.雍恩米［6］将该问题转化成几种极限情况下的轨迹优化问题，然后采用高斯伪谱法进行优化求解，最后将极限轨迹的终点用直线连接，采用多边形来近似可达区域.李瑜［7］则将该问题转化成多种情况下的轨迹优化问题，然后采用直接打靶法进行求解，最后获得可达区域.

不同于上述解决方法，本文将升力式再入飞行器的覆盖范围生成问题转化成满足再入约束条件下的最大纵程、最小纵程、最大横程以及一定纵程下最大横程的轨迹优化问题.首先给出了覆盖范围的分析步骤，建立了升力式再入飞行器的运动模型，给出了覆盖范围各类轨迹优化问题的优化模型，然后采用序列梯度－修复算法来解这一系列的轨迹优化问题，最后进行了仿真分析，并给出了相应的仿真结果.

1 问题的描述

采用本文的分析方法其相应分析步骤为:

1)解满足再入约束条件下的最大纵程的轨迹优化问题，获得升力式再入飞行器的最大纵程;

2)解满足再入约束条件下的最小纵程的轨迹优化问题，获得升力式再入飞行器的最小纵程;

3)解满足再入约束条件下的左边最大横程的轨迹优化问题，获得升力式再入飞行器左边的最大横程和该横程所对应的纵程;

4)在最小纵程和左边最大横程所对应的纵程之间取若干纵程，采用相应的优化模型，优化该特定纵程情况下的左边最大横程;

5)在左边最大横程所对应的纵程和最大纵程之间取若干纵程，采用相应的优化模型，优化该特定纵程情况下的左边最大横程;

6)以左边最大横程的倾侧角的相反数为初值，解满足再入约束条件下的右边最大横程的轨迹优化问题，获得升力式再入飞行器右边的最大横程和该横程所对应的纵程;

7)在最小纵程和右边最大横程所对应的纵程之间取若干纵程，采用相应的优化模型，以左边该特定纵程的倾侧角的相反数为初值，优化该特定纵程情况下的右边最大横程;

8)在右边最大横程所对应的纵程和最大纵程之间取若干纵程，采用相应的优化模型，以左边该特定纵程的倾侧角的相反数为初值，优化该特定纵程情况下的右边最大横程;

9)连接最大纵程弹道、最小纵程弹道、左边最大横程弹道、右边最大横程弹道和各特定纵程下最大横程弹道的终点，各最优轨迹的终点所组成的区域即为升力式再入飞行器的覆盖范围.

基于上述分析，下面将分别给出升力式再入飞行器的运动模型和分析覆盖范围中各类轨迹优化问题的优化模型.

1.1 升力式再入飞行器的运动学模型

为增强优化算法的鲁棒性，提高优化速度，应采用无量纲化的再入运动学模型.将飞行器再入运动学模型中的相关量除以相应的无量纲化系数，得到相应的无量纲化方程为

图1 纵横程定义

1.2 覆盖范围分析的轨迹优化模型

1)性能指标J.

当求取最大纵程时，

当求取最小纵程时，

当求取右边最大横程时，

当求取左边最大横程时，

2)优化控制量u(t).由升力式再入飞行器的控制方式可以得到其优化控制量u(t)如下:

3)约束条件.攻角α约束为

倾侧角σ约束为

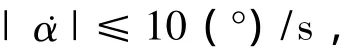
滑翔段最大高度hmaxh约束为

动压q约束为

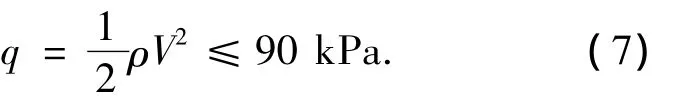
式中V为飞行器相对大气的速度.

法向过载ny约束为

式中N为体系下的法向力.

式中:Rn为鼻锥驻点区曲率半径;V0为第一宇宙速度;ρ0为海平面标准大气密度;ks、m、n为常数，可取理论计算值或实验值，本文取ks=17 600，n=0.5，m=3.15，Rn=0.04 m.

末端高度约束为

末端速度约束为

当求取最小纵程和最大横程所对应的纵程之间某一固定纵程Ldc所对应的最大横程时，应加入如下纵程固定的约束:

当求取最大横程所对应的纵程和最大纵程之间某一固定纵程Ldc所对应的最大横程时，相应的纵程固定约束变为

2 序列梯度－修复算法理论

序列梯度－修复算法是由Miele［8］在1970提出的一种求解最优控制问题的间接法.而后不断发展完善，形成了能够处理各种过程约束和边界约束的标准化序列 －梯度优化算法［9－14］.该算法由梯度和修复两个环节组成，采用统一的最优性条件，减少了推导伴随方程与横截条件等过程的复杂和繁琐，便于模块化实现.同时，由于修复环节的存在，该方法对初值不敏感.本文将采用序列梯度－修复算法来解升力式再入飞行器覆盖范围分析的轨迹优化问题.

2.1 最优控制问题的一般描述

不失一般性，取如下目标函数求取最小值:

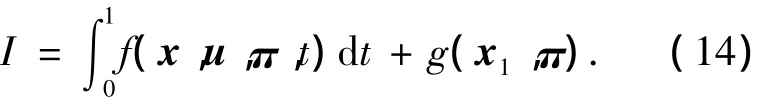
状态方程:

初始条件:

终端约束:

过程约束:

式中:性能指标I由积分型函数f和末端型函数g组成;x为状态变量;φ为状态微分函数;u为控制变量;π为参数向量;ψ为终端约束函数;t为时间变量;S为过程约束;x1表示状态量的末端值;x0表示状态量的初值;C0为x初值的给定值;对于任意积分区间tf，可将tf当成参量，通过相应地转化均可化成0～1区间.

对于1.2节中的轨迹优化模型，式(14)～式(18)的含义为:性能指标I即代表式(2)～式(5)中的某一式，且均为末端型函数，也即对于式(2)～式(5)f为零，g为式(2)～式(5)中的右边项;状态变量x为式(1)的左边项，状态微分函数为式(1)的右边项;控制变量u为攻角α和倾侧角σ;参数向量π为tf;终端约束函数ψ为式(10)～式(13);过程约束S为式(6)～(9).同时需要注意的是序列梯度－修复算法仅能处理等式约束，因此对于不等式约束只需要引入辅助变量化成等式约束即可，具体转化过程可参见文献［14］.

2.2 一阶最优必要条件

应用最优控制理论，通过欧拉方程可以得到

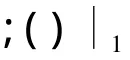
2.3 一阶梯度近似

式中Δx(t)、Δu(t)、Δπ分别为状态量x(t)、控制量u(t)、参量π的增量.

现定义列向量A、B、C如下

则可以得到2.1节中最优控制问题的一阶梯度近似模型，为［9］

2.4 修复方法

则可以得到相应的修复模型如下［9］:

为此通过一定的方法，不断地求解上式修复模型，并合理地搜索修复步长，定能找到在一定精度范围内满足式(15)～式(19)的状态量、控制量和参量［11］.

3 优化算法结构

结合具体的飞行器优化模型，采用本文给出的序列梯度－修复算法优化飞行器满足再入约束条件下的最大纵程、最小纵程、最大横程以及一定纵程下最大横程的最优轨迹，相应的算法结构如下.

1)由于算法中修复环节的存在，算法对初值不敏感.首先由系统的相关知识，给出u(t)在初始点、末端点的值以及π的值，然后根据积分点数，由u(t)初始点值和末端点值线性插值得到中间点值，最后积分状态方程式(15)得到x(t)，从而获得x(t)、u(t)、π的初值.

3)采用文献［14］中的方法解修复模型式(27)～ 式(34)获得的 A(t)、B(t)、λ(t)、ρ(t)，再采用二分法搜索修复步长，获得新的状态量否满足式(15)～式(18)，若满足则修复阶段结束，进入步骤4);否则，将的值赋给x(t)、u(t)、π进入步骤3)，重复进行修复阶段，直到式(15)～式(18)得到满足.

5)判断整个迭代是否收敛，若收敛则优化结束，输出相应数据，否则继续迭代.收敛的判断准则为当前得到的控制量和参量的值相对于前一步得到的值的增量小于一给定的小量.

4 覆盖范围仿真分析

考虑到飞行器在高空飞行时由于气动力较小，其相应的机动能力较低，同时为了减少计算量提高优化速度，飞行器从120 km再入至飞行路径角变为零的阶段采用常值大攻角和零倾侧角进行轨迹积分获得其纵程和横程，剩余轨迹则采用本文的方法进行优化.本文的仿真初始条件为:初始高度74.84 km，初始速度为6 603.02 m/s，飞行路径角为0.结合飞行器的总体参数，采用无量纲化方程(1)以及1.2节中的轨迹优化模型，应用序列梯度－修复算法，按第1节中的优化步骤进行优化分析，得到再入飞行器的覆盖范围分析结果如下图2～7所示.

图2 再入速度曲线

图3 法向过载曲线

图4 动压曲线

图5 驻点热流曲线

图6 三维轨迹

图7 纵横程曲线

从图2～5中可以看出:所有轨迹的末端速度均为2 000 m/s;所有轨迹中的最大法向过载为3.002，其余均小于等于3.0;所有轨迹中的最大动压为91.6 kPa，其余均小于等于90.0 kPa;所有轨迹的最大驻点热流为2 583.0 kW/m2，其余均≤2 500.0 kW/m2;在误差范围内所有轨迹均满足相应约束的要求.同时由图6可以看出为了获得较大的纵程和横程，在气动特性允许的范围内飞行器采用跳跃的轨迹飞行，但跳跃的最大高度均≤65 km，且由图7可以得到具体优化结果如下:

1)优化满足再入约束条件下的最大纵程轨迹，得到再入飞行器的最大纵程为12 680 km;

2)优化满足再入约束条件下的最小纵程轨迹，得到再入飞行器的最小纵程为2 616 km;

3)优化满足再入约束条件下的左边最大横程轨迹，得到再入飞行器的左边最大横程为－4 721.2 km，其对应的纵程为6 237.0 km;

4)以左边最大横程所对应的纵程为分界点分别取固定纵程 4 525.6、7 936.2、9 552.8、10 843.0和11 783.0 km，分析其对应的左边最大横程，如图7所示;

5)以左边最大横程轨迹为参考，优化右边最大横程轨迹，得到再入飞行器右边的最大横程为5 026.4 km;

6)以左边最大横程轨迹为参考，优化固定纵程 4 525.63、7 936.2、9 552.8、10 843.0 和11 783.0 km对应的右边最大横程，如图7所示;

同时，从图6中可以看出，由于地球的自转影响，升力式再入飞行器的覆盖范围为1个左右不对称的扇形区域.依据椭圆面积公式大概可以估算得到其覆盖范围的面积约为7.226×107km2，合7 226万平方公里.

4 结论

本文将再入飞行器的覆盖范围生成问题转化成满足再入约束条件下的最大纵程、最小纵程、最大横程以及一定纵程下最大横程的轨迹优化问题.并采用序列梯度－修复算法来解这一系列的轨迹优化问题，最终得到了再入飞行器的覆盖范围.从整个问题的解决过程中可以看出:

1)本文给出的覆盖范围生成步骤合理可行;

2)采用序列梯度－修复算法能够对覆盖范围生成这一类轨迹优化问题进行优化分析，并具有较好的优化效果;

3)升力式再入飞行器的覆盖范围为1个左右不对称的扇形区域.

［1］NGO A D，DOMAN D B.Footprint determination for reusable launch vehicles experiencing control effector failures［R］.Rston，VA:AIAA，2002，AIAA －2002 －4775.

［2］LU P，XUE S B.Rapid generation of accurate entry landing footprints［R］.Rston，VA:AIAA，2009，AIAA－2009－5772.

［3］HARPOLD J C，GRAVES C A.Shuttle entry guidance［R］.Washington，DC:NASA，1979，NASA － TM －79949.

［4］SARAF A，LEAVITT J A，MEASE K D.Landing footprint computation for entry vehicles［R］.Reston，VA:AIAA，2004，AIAA－2004－4774.

［5］JACKSON M C，STRAUBE T M，FILL T J，et al.Onboard determination of vehicle glide capability for the shuttle abort flight manager(SAFM)［R］.Piscataway:IEEE，2002.

［6］雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究［D］.长沙:国防科技大学，2008.

［7］李瑜.助推－滑翔导弹弹道优化与制导方法研究［D］.哈尔滨:哈尔滨工业大学，2009.

［8］MIELE A，PRITCHARD R E，DAMOULAKIS J N.Sequential gradient-restoration algorithm for optimal control problems［J］.Journal of Optimization Theory and Applications，1970，5(4):235 －282.

［9］MIELE A，DAMOULAKIS J N，CLOUTIER J R，et al.Sequential gradient-restoration algorithm for optimal control problems with nondifferential constraints［J］.Journal of Optimization Theory and Applications，1974，13(2):218－255.

［10］GONZALEZ S，MIELE A.Sequential gradient-restoration algorithm for optimal control problems with general boundary conditions［J］.Journal of Optimization Theory and Applications，1978，26(3):395 －425.

［11］ROM M，AVRIEL M.Properties of the sequential gradient-restoration algorithm(SGRA)，part 1:introduction and comparison with related methods［J］.Journal of Optimization Theory and Applications，1989，62(1):77 －98.

［12］ROM M，AVRIEL M.Properties of the sequential gradient-restoration algorithm(SGRA)，part 2:convergence analysis［J］.Journal of Optimization Theory and Applications，1989，62(1):99 －125.

［13］MIELE A，WANG T.Multiple-subarc gradient-restoration algorithm，part 1:algorithm structure［J］.Journal of Optimization Theory and Applications，2003，116(1):1－17.

［14］MIELE A，WANG T.Multiple-subarc gradient-restoration algorithm，part 2:application to a multistage launch vehicle design［J］.Journal of Optimization Theory and Applications，2003，116(1):19 －39.

Calculation of reachable landing locations of lift entry vehicle

FU Yu1，YANG Wei-li2，CUI Nai-gang1

(1.School of Astronautics，Harbin Institute of Technology，150001 Harbin，China;2.Defense Technology Information Center，100142 Beijing，China)

In this paper，the problem of reachable landing locations generation is transformed into trajectory optimization of maximum downrange，minimum downrange，maximum crossrange and maximum crossrange at specified downrange under entry constraints，and the sequential gradient-restoration algorithm is used to solve the trajectory optimization problem.Numerical simulations are performed，and the simulation results show that the technology of reachable landing locations generation for lift entry vehicle is reasonable and feasible，and the reachable landing locations generation of lift entry vehicle is left-right asymmetry fan-shaped region.

lift entry vehicle;reachable landing locations;trajectory optimization;sequential gradient-restoration algorithm

V412

A

0367－6234(2012)11－0013－07

2011－10－11.

国防重点学科实验室基金资助项目(HIT2009093).

傅 瑜(1985—)，男，博士研究生;

崔乃刚(1965—)，男，教授，博士生导师.

傅 瑜，fuyulucky13@163.com.

book=19,ebook=265

(编辑 张 宏)