粒子滤波在卫星姿态确定中的应用
张 健,孙兆伟
(哈尔滨工业大学卫星技术研究所,150001 哈尔滨)
粒子滤波在卫星姿态确定中的应用
张 健,孙兆伟
(哈尔滨工业大学卫星技术研究所,150001 哈尔滨)
为了验证以星敏感器和速率陀螺作为卫星测量元件时,粒子滤波算法在姿态确定中的有效性.采用修正的罗德里格参数作为姿态参数建立了有陀螺和无陀螺两种模式下的系统状态方程和测量方程,并利用粒子滤波(PF)算法进行了姿态估计.和扩展的卡尔曼滤波(EKF)算法进行比较,仿真结果表明:PF算法在小初始估计误差下能够收敛,且具有和EKF相当的精度.大初始估计误差时,EKF算法不能收敛而PF算法仍能收敛.最后验证了PF算法在无陀螺模式下进行姿态确定的有效性.
粒子滤波;姿态确定;星敏感器;速率陀螺
卫星姿态确定系统作为控制的前提,其精度直接影响到姿态控制的质量.目前,EKF算法作为非线性滤波的经典算法,在卫星姿态确定中被广泛的应用.然而,EKF算法需要对非线性的状态方程和测量方程进行线性化,并需要计算雅克比行列式,计算复杂鲁棒性低.粒子滤波算法是基于贝叶斯最优估计理论和蒙特卡洛积分原理来对状态的后验概率密度函数进行近似,能够克服EKF 的缺点[1-3].程杨等[4]利用粒子滤波算法,结合修正的罗德里格参数对卫星姿态进行估计,克服了四元数用于姿态估计时需要满足四元数归一化的约束问题,引入变化的协方差矩阵,克服了由于观测误差很小引起的样本快速枯竭的问题.Oshman等[5]将粒子滤波算法和遗传算法相结合,用于有陀螺工作下的卫星姿态确定,其算法结合了遗传算法和例子滤波算法,虽然滤波精度有所提高,但计算量很大.姜雪原等[6]把 Rao-Blackwellization技术和粒子滤波结合,提出基于Marginalized的粒子滤波算法,并用于卫星姿态估计,取得了较好的效果.本文采用由Gordon等[7]提出的Bootstrap粒子滤波(BF)算法,对卫星的姿态确定问题进行了仿真研究,并针对有陀螺模式下粒子滤波算法出现的样本枯竭问题,对粒子滤波进行改进,引入扩展的卡尔曼粒子滤波(EKPF)算法,结果证明其可行性.最后利用粒子滤波算法对无陀螺模式下的姿态确定问题进行了仿真分析,验证了其有效性.
1 系统状态方程
本文针对有陀螺和无陀螺两种模式,采样修正的罗德里格参数作为状态参数,分别建立了系统的状态方程.
假设卫星为一单刚体,则用修正的罗德里格参数表示的运动学方程为
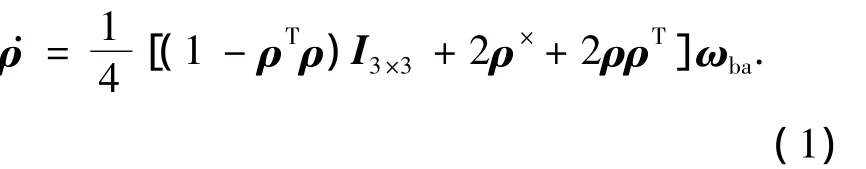
式中:ρ = [ρx,ρy,ρz]T为修正的罗德里格参数;I3×3为3阶的单位阵;ωba为体系相对于参考系的角速度;ρ×为ρ的叉乘矩阵,表示为
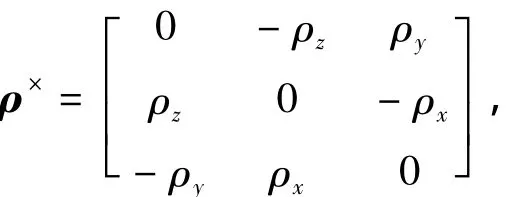
动力学方程为

式中:I为卫星在星体固联坐标系的转动惯量矩阵;T为作用在星体上的内外力矩的分量列阵.

陀螺测量模型采用简单的Farrenkopf模型,可表示为式中:ωbi为卫星相对于惯性空间的旋转角速度;ωg为陀螺测量的角速度;b为陀螺常值漂移;vg为陀螺测量的白噪声,满足vg~N(0,σ2g);vb为驱动陀螺常值漂移的白噪声,满足vb~N(0,σ2b).
1.1 有陀螺模式下的状态方程
有陀螺模式下选择修正的罗德里格参数和陀螺漂移作为状态变量,即

式中:b= [bx,by,bz]T为陀螺漂移.则根据方程(1)和(3)可得系统的状态方程为

式中:W为系统噪声,这里假设为零均值的高斯噪声,f(x,t)为非线性函数,有
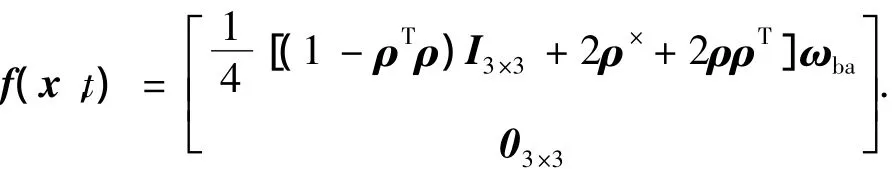
1.2 无陀螺模式下的状态方程
无陀螺模式下用卫星动力学方程来代替陀螺测量方程,选择修正的罗德里格参数和角速度作为状态变量,即则根据方程(1)和方程(2)可得系统的状态方程为方程(4)表示的形式,其中f(x,t)为

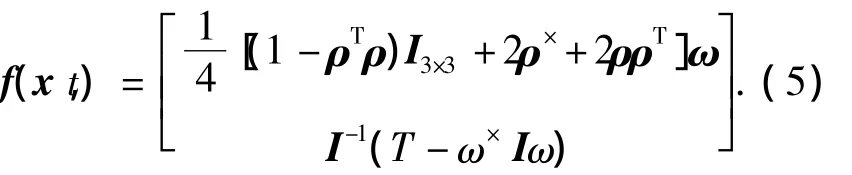
2 测量方程
星敏感器是一种以恒星为姿态参考的高精度光学敏感器,是航天器姿轨控系统中常用到的敏感元器件.由筒镜光学系统和CCD面阵光敏元器件组成,来自星光的平行光经过光学系统,在CCD面阵上聚焦成像圈[8].如图1所示,定义星敏感坐标系Oxsyszs,zs轴沿中心光轴,xs和 ys轴沿CCD面阵的正交基准,(px,py)为星光像元在面内的坐标,f为光学系统的焦距.
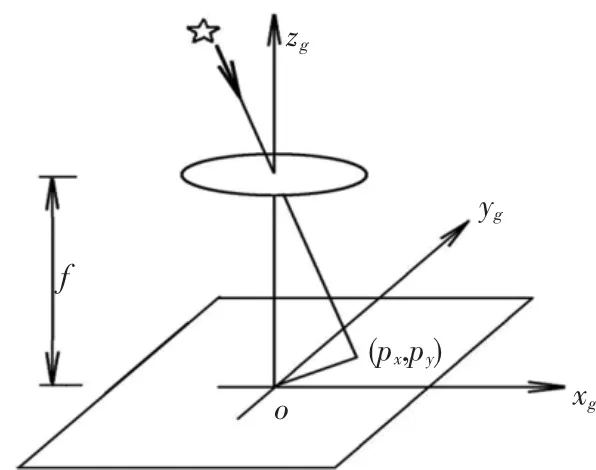
图1 星敏感器测量原理图
假设星敏感器坐标系与星体坐标系重合,且光轴沿星体zb轴方向.用p=[px;py]表示星光矢量ri在CCD平面上成像点的真实坐标,记为

定义惯性空间中相对于某个恒星天体的两个平行的参考矢量的观测值分别为ui1和ui2,则可以建立星敏感器的测量模型为
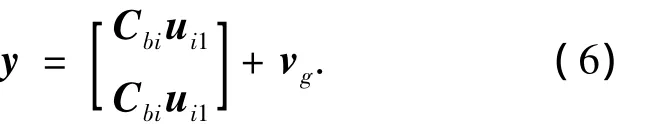
式中:Cbi为惯性系到体系的坐标变换矩阵;vg为星敏感器的测量噪声.为便于分析,采用:ui1=[1,0,0]T,ui1= [0,1,0]T.
3 粒子滤波算法在姿态确定中的应用
所谓粒子滤波是指:通过寻找一组在状态空间中传播的随机样本,对概率密度函数p(xk|zk)进行近似,以样本均值代替积分运算,从而获得状态的最小方差估计的过程,是一种基于贝叶斯估计思想的非线性滤波算法.当粒子数目足够大时,这些样本点能非常接近地表征后验概率密度.
Gordon等人提出 Bootstrap粒子滤波算法(BF),由于应用简单得到了广泛应用,其基本步骤如下:
1)初始化.从p(x0)中随机抽取N个样本,xi0~ N(0,^P(x0)),wi0=1/N,i=1,2,…,N,其中N为粒子数.
2)递推计算,k=1,2,….
3)重要性抽样,从q(xk|xk-1,zk)中随机抽取N个样本,利用公式(7)计算权值,并利用公式(8)进行归一化,
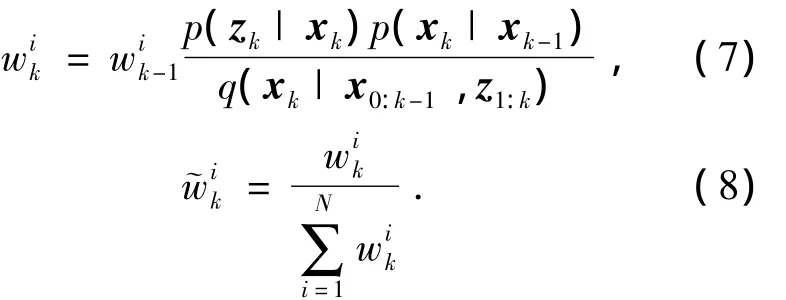
4)重采样.由公式(9)计算有效粒子数[10],并与预定的阀值粒子数比较判断是否需要进行重采样.若Neff<Nth,则进行重采样;其中Nth为重采样的阀值粒子数,取Nth=2/3N,否则转步骤5;

5)输出估计值.BF粒子滤波算法采用的重要性函数是次优的,并且没有充分利用当前的测量信息.为得到更为精确的重要性函数,在粒子一步更新阶段引入EKF过程,通过EKF对所有粒子进行一步更新,在加权求均值和协方差,即得到扩展的卡尔曼粒子滤波(EKPF).EKPF算法和BF算法相比,在粒子更新阶段充分利用了当前的测量信息,能得到更好的估计效果[11].这里采用修正的罗德里格参数作为卫星姿态参数,和四元数相比,没有约束条件,其协方差矩阵非奇异[12].根据有陀螺和无陀螺两种模式下得到的状态方程和测量方程,选择不同的状态估计初值和协方差矩阵,利用上述的粒子滤波算法进行状态估计.
4 数学仿真
模式一:
有陀螺模式,仿真参数为
1)假设卫星星体处于没有控制力矩,只受到外界干扰力矩作用的状态,仿真过程中假设外加的干扰力矩矢量为 Td= [10-5;10-5;10-5]N·s;
假设卫星星体的转动惯量矩阵为I=diag(100,200,200)kg·m2;
2)姿态角和角速度初值分别为φ=0°,θ=0°,Ψ =0°;wx0=0(°)/s,wy0=0(°)/s,wz0=0(°)/s;

4)星敏感器测量噪声的均方差为σp=100 urad;星敏感器的采样周期为1 Hz;仿真步长取1 s.
估计初值:①小初始估计误差:姿态角估计值设为[1,1,1]°,陀螺漂移估计值设为[2,2,2](°)/h,姿态方差为(1°)2,初始陀螺漂移的方差为(1(°)/h)2,采样粒子数为1 000;②初始的姿态角初值设为[12,-10,170]°,其他同上;由图 2可知,在小初始估计误差情况下使用粒子滤波算法,姿态角估计估计误差能够收敛,但陀螺漂移估计误差不能够收敛,而是在初值附近的某个值上下波动.这是因为陀螺漂移的递推过程是一个静态的传播过程,即bk+1=bk,这样在粒子滤波过程中经过几次重采样过程后,所有粒子点几乎全部集中在一个粒子上,造成样本枯竭现象,达不到滤波效果.
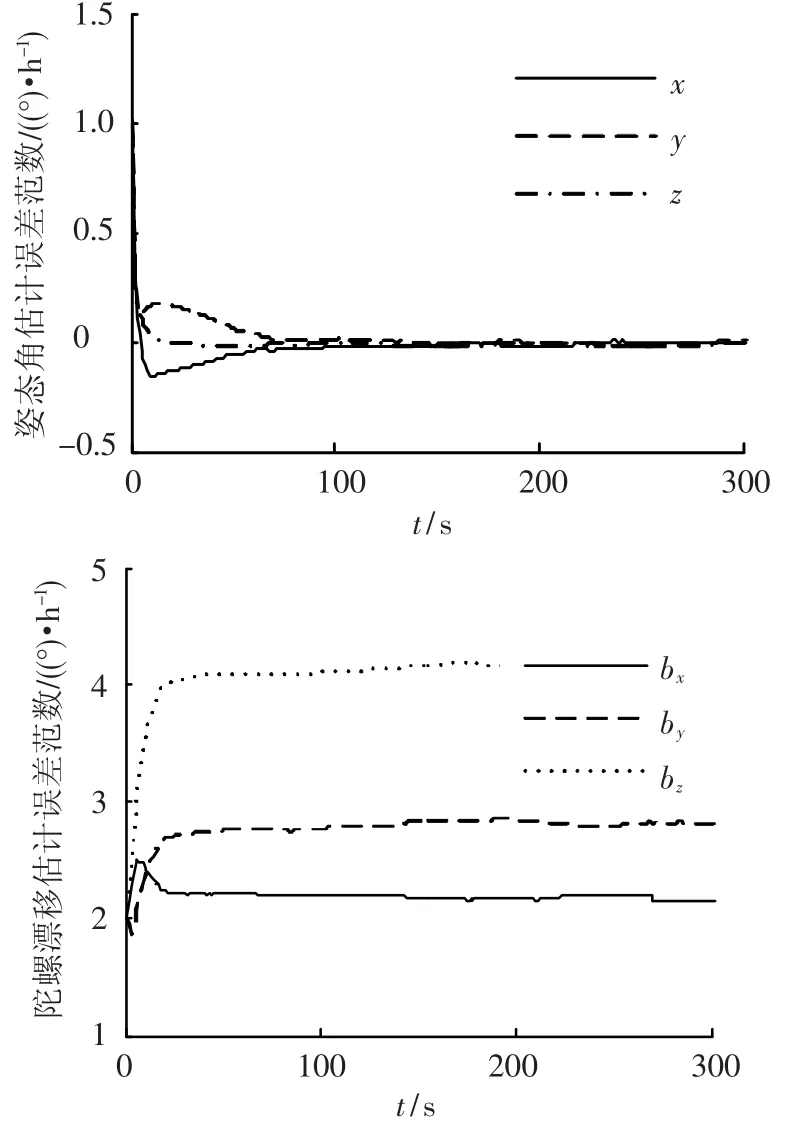
图2 陀螺模式下小初始估计误差PF姿态角误差和陀螺漂移估计误差曲线
由图3可知,用EKPF算法对小初始估计误差的情况状态进行估计,姿态角和角速度的收敛精度分为 0.002°和 0.000 05(°)/s.说明在小初始估计误差的情况下,EKPF算法和EKF算法都能够收敛,具有相同的精度.但EKPF算法计算量大,不适合用于实时状态估计.
由图4和图5可知,在大初始估计误差的情况下,EKPF算法还能保持收敛,但EKF算法就变得发散了.这也体现了EKPF算法在状态估计中的优势.
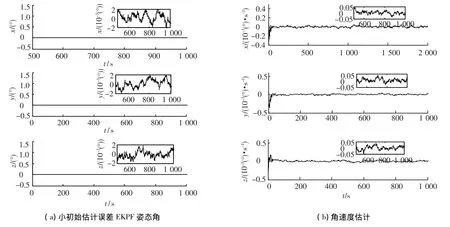
图3 有陀螺模式下小初始估计误差EKPF姿态角和角速度估计误差曲线

图4 有陀螺模式下大初始估计误差EKPF姿态角和陀螺漂移估计误差范数曲线

图5 有陀螺模式下大初始估计误差EKF姿态角和陀螺漂移估计误差范数曲线
模式二:无陀螺模式
仿真参数为:姿态角估计值设为[1,1,1]°,角速度估计初值设为[0.001,0.001,0.001](°)/s,姿态方差为(1°)2,角速度的方差为(0.001(°)/s)2,采样粒子数为1 000,其他同有陀螺模式下得仿真参数设置.
图6表明,粒子滤波在无陀螺模式下,姿态角估计精度为0.01°,角速度估计精度为0.004(°)/s,虽然和有陀螺时相比,精度降低,但仍能满足一般精度要求的卫星.

图6 无陀螺模式下BF姿态角和角速度估计误差曲线
5 结论
本文对粒子滤波算法及其在卫星姿态估计中的应用进行了研究.结果表明:在有陀螺模式下,当直接使用粒子滤波算法时,由于重采样过程引起了样本枯竭,陀螺漂移不能收敛;为此采用EKPF算法,可以缓解样本枯竭的现象,姿态角和陀螺漂移都可以收敛,且具有和EKF算法相同的估计精度.另外,采用粒子滤波算法的优势主要体现在初始估计误差较大的情况下,估计结果仍然可以收敛.最后,在无陀螺情况下,用卫星动力学模型代替陀螺测量模型,结果表明仍能达到一定精度的估计精度,适用于一般精度要求的卫星姿态确定.
[1]MOHD POINT KEUI A A,FADLY M,SIDEK O.EKF implementation on S3CEV40 for Inno SAT attitude determination system[C]//2011 Internation Conference on Computer Applications and Industrial Electronics,Penang,MALAYSIA:IEEE,[s.n.],2011:373 -378.
[2]HUANG Guoquan P.MOURIKIS A I,ROUMELITIOTIS S I.A First-Estimates Jacobian EKF for improving SLAM Consistency[C]//Proceedings of the International Symposium on Experimental Robotics(ISER),Athens,Greece:[s.n.],2008:373 -382.
[3]SOKEN H E,HAJIYEV C.REKF and RUKF development for pico satellite attitude estimation in the presence of measurement faults[C]//Recent Advances in Space Technologies(RAST),2011 5th International Conforence on,Istanbul:IEEE,2011:891-896.
[4]CHENG Y,CRASSIDIS J.Particle filtering for sequential spacecraft attitude estimation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,Providence,American Intstitute of Aeronautics and Astronautics.Rhode,Island:[s.n.],2004:2004 -5337.
[5]OSHMAN Y,CARMI A.Spacecraft attitude estimation from vector observations using a fast particle filter[J].Advances in the Astronautical Sciences,2005,Suppl 119:593-607.
[6]姜雪原,马广福,胡庆雷.基于Marginalized粒子滤波的卫星姿态估计算法[J].控制与决策,2007,22(1):39-44.
[7]GORDON N,SALMOND D.Novel approach to non-linear and non-gaussian Bayesian state estimation [J].Proceedings of Institude Electric Engineering,1993,40(2):107-113.
[8]孙兆伟,李晖,张世杰.仅用星敏感器的卫星姿态估计UKF算法研究[J].飞行力学,2006,24(3):56-60.
[9]LIU J S,CHEN R.Sequential monte carlo methods for dynamic system[J].Journal of the American Statistical Association,1998,443(93):1032-1044.
[10]王晨,房建成.基于Unscented四元数粒子滤波的微小卫星姿态估计[J].北京航天航空大学学报,2007,33(5):552-556.
[11]牟忠凯,隋立芬,黄贤源.基于UPF的修正的罗德里格参数卫星姿态估计[J].中国空间科学技术,2009,29(6):45-50.
Satellite attitude determination based on particle filter
ZHANG Jian,SUN Zhao-wei
(Research Center of Satellite Technology,Harbin Institute of Technology,150001 Harbin,China)
In order to investigate the efficiency of attitude determination system using particle filter.The system state equation and measure equation of a satellite with star-sensors and gyros were established.And particle filter was used to estimate the attitude of satellite.The simulation results showed that the system can convergent not only for the small initial estimation error,but also for the big initial estimation error.But EKF can convergent only for the small initial estimation error.Finally,the effectiveness of PF applied to the gyro-free mode was also verified.
particle filter;attitude determination;star-sensor;rate gyro
V19
A
0367-6234(2012)11-0031-05
2012-02-13.
张 健(1988—),男,硕士研究生;
孙兆伟(1963—),男,教授,博士生导师.
张 健,zhangjian6140@126.com.
(编辑 苗秀芝)

