基于粒子滤波的通信保障航天器相对导航方法

刘雪奎，孙兆伟，张 健，邓 泓

（哈尔滨工业大学卫星技术研究所，150080 哈尔滨）

基于粒子滤波的通信保障航天器相对导航方法

刘雪奎，孙兆伟，张 健，邓 泓

（哈尔滨工业大学卫星技术研究所，150080 哈尔滨）

为提高通信保障航天器天线指向精度，提出一种基于粒子滤波的通信保障航天器相对导航方法，获得两个航天器间更精确相对位置和速度.该方法利用测量距离远、覆盖率高和可全天候工作的无线电设备为主要测量部件，利用粒子滤波在非线性系统滤波上的优势，进行相对位置和速度的估计.仿真结果表明，新算法能够有效降低测量误差，提高相对位置和速度估计精度，保证通信保障航天任务的有效进行.

粒子滤波;相对导航;通信保障;在轨服务

通信保障航天器作为一种在轨服务航天器［1－2］，其主要任务是利用自身设备为空间通信故障航天器建立星地通信链路.通信保障航天器通过机动飞行到达故障航天器通信覆盖区域，与故障航天器构成飞行编队，并为其提供与地面的通信中继服务.航天器编队功能的实现，依赖于星间相对位置、速度的确定精度.因此，相对位置、相对速度的确定是卫星编队飞行和通信保障有效进行的关键技术之一.

常用的编队卫星相对位置确定方法包括地面测控站及中继卫星法、伪卫星相对定位技术、GPS、激光测量法、红外测量法、可见光测量法和无线电测量法等［3］.地面测控站及中继卫星法测量精度低，反应时间慢，不能用于卫星间的自主协同控制;伪卫星相对定位技术需建立大量的地面发射系统且实用性差;GPS测量技术的隐蔽性差，存在重大安全因素，因此，此测量方式在我国军事应用上受到限制;激光测量保密性好，抗干扰能力强，测量精度高，但其功率大，波束狭窄，需要别的测量系统进行引导;红外测量仅能提供目标的角度测量信息，不能单独实现卫星的相对状态测量;可见光测量仅适用于近距离测量，且在光照较强的环境下，测量精度较差;采用星间无线电测量，作用距离远、测量覆盖率高、测量精度高、实时性强，可全天候工作，且在测量的同时具有信息通信功能，满足小型化、低功耗、多航天器相对测量的要求［4］.鉴于无线电测量的各项优点，本论文将采用无线电测量法进行通信保障航天器和故障航天器的相对位置和相对速度测量.

为降低无线电测量设备误差的影响，采用粒子滤波(Particle Filter，PF)方法对测量结果进行修正，提高相对位置和速度测量精度，从而为通信保障航天器的有效工作提供基础.

本文以通信保障航天器和故障航天器组成的空间编队为研究背景，对航天器间的相对位置确定算法进行研究.首先建立编队飞行卫星相对轨道运动数学模型，并对两种主要相对轨道构型进行研究，然后利用基于无线电测量方法测得的星间基线信息，结合粒子滤波(PF)算法确定卫星间的相对位置和速度.

1 系统状态方程

参考坐标系OIXIYIZI原点OI定义在故障航天器的质心，OIYI沿地球的半径方向朝外，OIXI与OIYI垂直指向飞行的前方，OIZI与OIXI、OIYI构成右手坐标系［5］，如图1所示.

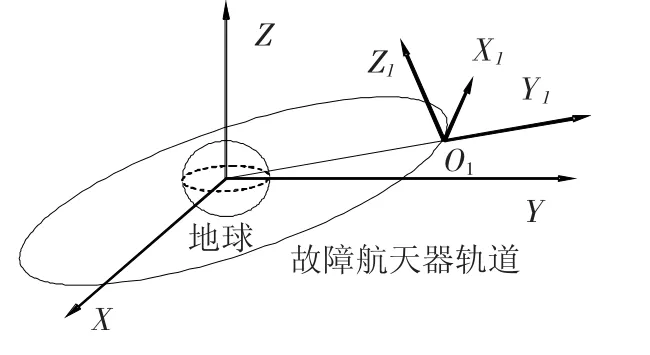
图1 相对轨道状态的参考坐标系

假设故障航天器的运行轨道为圆轨道，轨道半径为rc，则故障航天器的轨道角速度w为常值，且

根据相对运动规律，可得两航天器的相对运动方程(即希尔方程)为

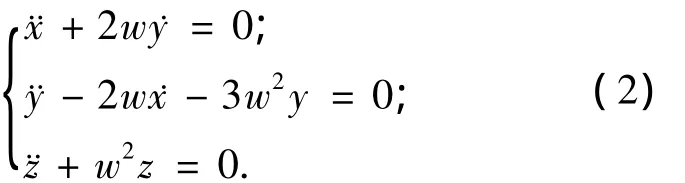
取状态变量为

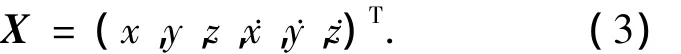
则把上述希尔方程写成系统的状态方程为

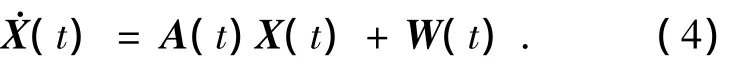
A(t)为状态转移矩阵，W(t)为过程噪声，

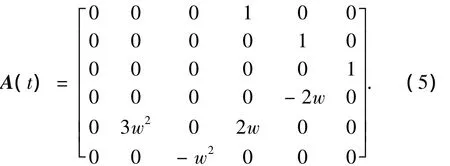
对上述状态方程进行离散化，得到离散的状态方程:Xk= φkXk－1+Wk－1，设采样周期为 T，当其足够小时，将状态方程离散化近似可得

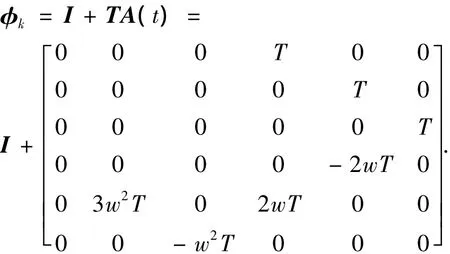
式中:I为6×6单位阵;T为采样时间.

2 无线电测量方程

利用无线电测量可得两航天器间基线的两个测量量:采用无线电测距测得星间基线长度;采用多天线比相法测得星间基线指向，即基线在参考坐标系中的方位角和仰角.

利用航天器上安装的无线电收发设备，通过测量无线电波在卫星间的传播时间获得星间距离测量值，并结合一定的数据处理方法确定小卫星间的相对状态［6－7］.

如图2所示，每航天器都定义体坐标系，其原点为该航天器的质心，接收天线和发射天线的安装坐标在各自本体坐标系中标定［8］.

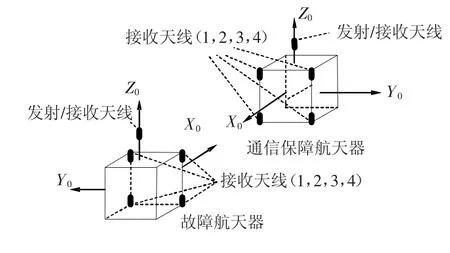
图2 航天器间基线无线电测量系统天线布局图

为方便描述，假定航天器是立方体，4个接收天线分别安装于正方体同一平面的4个顶点上，1个天线安装在Z轴正方向上，为发射/接收共用天线.

每个发射机向另外一颗航天器发射调制有传输数据的测距信号.通过信息交互和测量发射天线与接收天线相互之间的距离及角度，实现航天器间基线测量，以用来解算航天器间的相对位置和相对速度.采用双单程测距技术，可实现航天器间基线长度测量;采用比相测角技术，可实现航天器间基线指向的高精度测量.

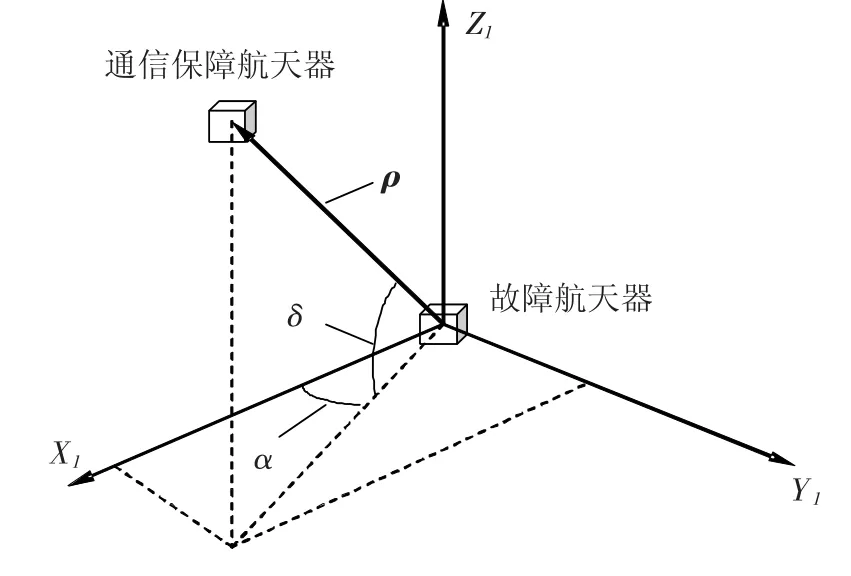
图3 测量坐标系

两个航天器相对距离矢量→—ρ在参考坐标系OIXIYIZI中的几何关系如图3所示，测量系统给出的相对位置信息为相对距离ρ，方位角α和仰角δ.其中，定义相对距离ρ为故障航天器到通信保障航天器的距离，即|→—ρ|;方位角α为两航天器相对距离矢量→—ρ在XΙYΙ平面投影与OIXI轴夹角(0 ～2π)，仰角 δ为双星相对距离矢量→—ρ 和XΙYΙ平面的夹角(－ 0.5π ～ 0.5π).根据测量的几何关系可得到相对距离ρ，方位角α和仰角δ的表达式

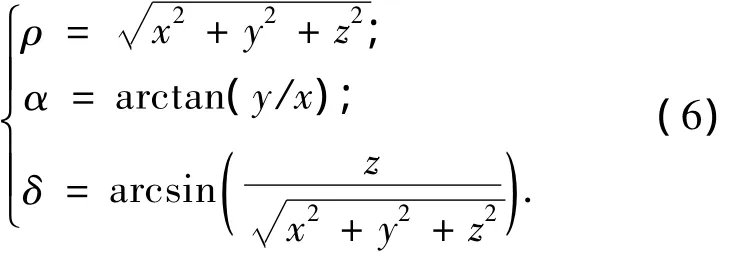
由(6)式可得出［9］

因此，测量值(ρ，α，δ)与(x，y，z)间为非线性关系.将测量值(ρ，α，δ)作为输出量，则测量方程为

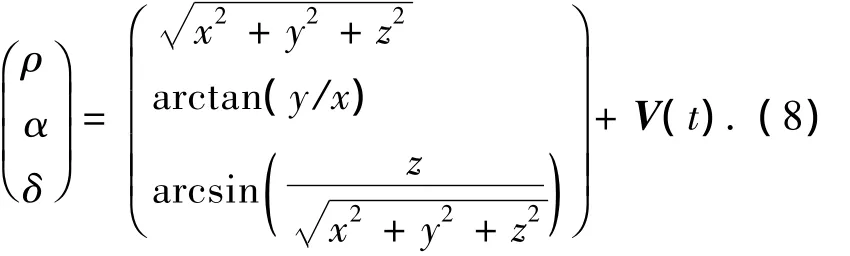
取观测量为 y=(ρ，α，δ)T，则可得相应的观测方程为

其中g(x)为测量方程，V为观测噪声.

3 粒子滤波过程

粒子滤波是基于蒙特卡洛方法和递推贝叶斯估计的统计滤波方法，其基本思想是:首先依据系统状态向量的经验条件分布在状态空间产生一组随机样本的集合，即为粒子，然后根据测量不断调整粒子的权重和位置，通过调整后的粒子信息修正最初的经验条件分布，对概率密度函数p(xk|yk)进行近似，以样本均值代替积分运算，从而获得状态的最小方差估计［10－11］.当所取的粒子数足够多时，这种滤波方法接近最优贝叶斯估计.

传统的扩展的卡尔曼滤波(EKF)、无迹滤波(UKF)是基于状态变量的分布服从高斯分布的，对状态变量的均值和协方差进行估计，而对于非高斯分布的系统，其滤波效果会明显下降，另外由公式(8)可知，在通信保障航天器无线电测量的观测方程为非线性方程，而粒子滤波方法作为一种基于贝叶斯估计思想的非线性滤波算法，在处理非线性、非高斯噪声系统的参数估计和状态滤波等方面具有一定优势［12］，因此本文将PF算法应用到两个航天器的相对导航中，能够取得较好效果.

本文根据得到的系统的状态方程和测量方程，应用“采样－重要性－重采样”结构的序贯重要性重采样粒子滤波方法进行数据处理，并利用多项式重采样算法来克服粒子滤波过程中出现的粒子匮乏现象.假设估计状态的初始分布已知，且为p(x0).

其步骤如下:

本文取重要性密度函数为:q(xk|x0:k－1，yk)=p(xk，xk－1)，这种方法虽然不是最优方法，但是容易实现，因此在处理实际问题中被广泛采用.

5)判断是否需要重采样:根据以下公式计算有效粒子数)Neff，若有效粒子数小于预定的阀值粒子数Nth，一般取2N/3，则进行步骤6，进行重采样过程，否则跳至步骤7，不进行重采样;

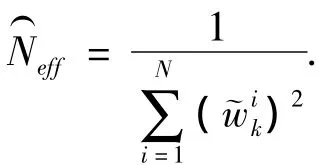
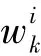
7)令k=k+1，转到步骤2)继续执行.

8)输出k时刻的状态和协方差的估计值

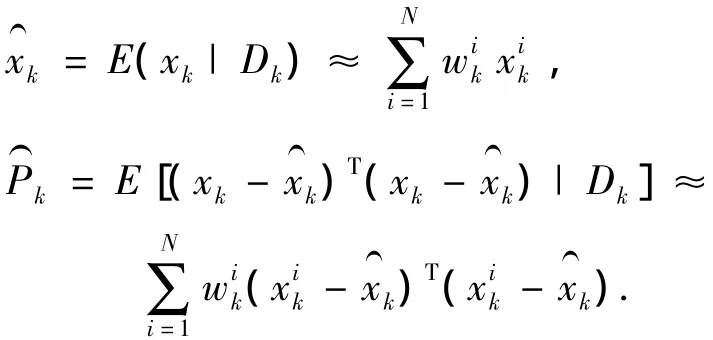
4 数值实例

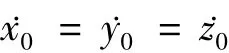
初始偏差状态为

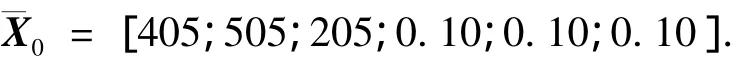
过程噪声协方差矩阵R为

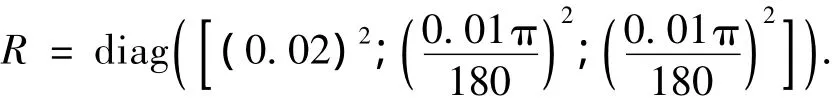
观测噪声协方差矩阵Q为初始误差矩阵P0为:

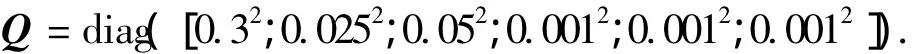
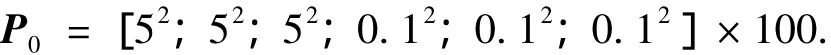
图4与图5分别给出了X、Y和Z轴相对位置和相对速度误差曲线，其中相对位置误差在0.4 m以内，相对速度误差在0.02 m/s以内.

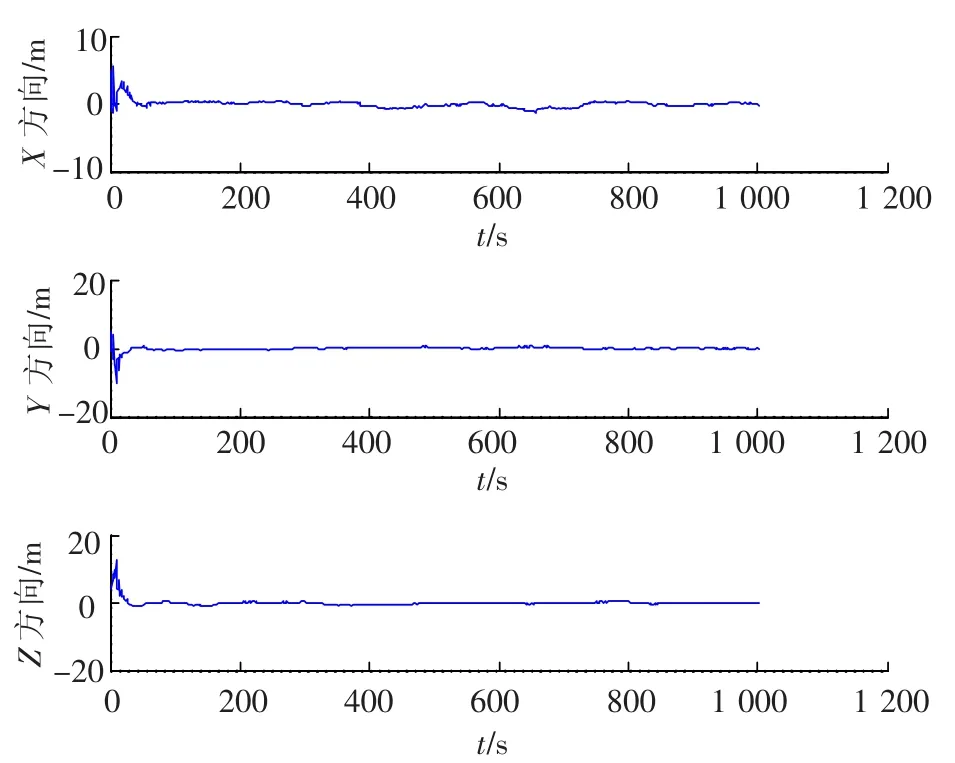
图4 相对位置误差曲线

图6和图7分别给出了故障航天器与通信保障航天器三轴相对位置误差和相对速度误差，从图中可以看出，X、Y和Z轴相对位置和速度经过80 s即可达到相对位置误差小于0.5 m，相对速度误差小于0.02 m/s.

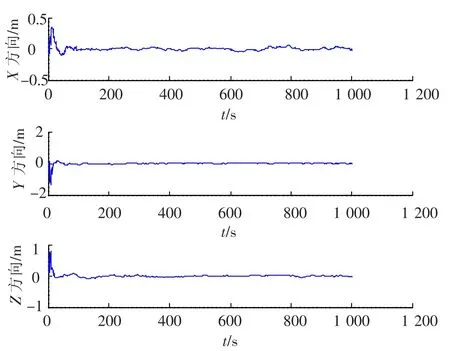
图5 相对速度误差曲线

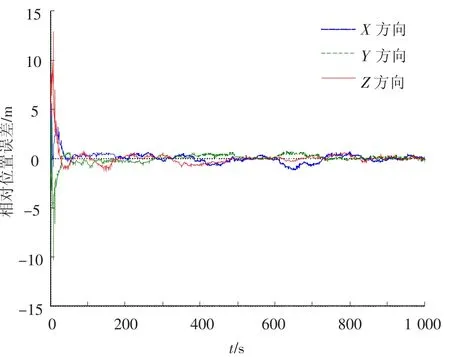
图6 三轴相对位置误差曲线

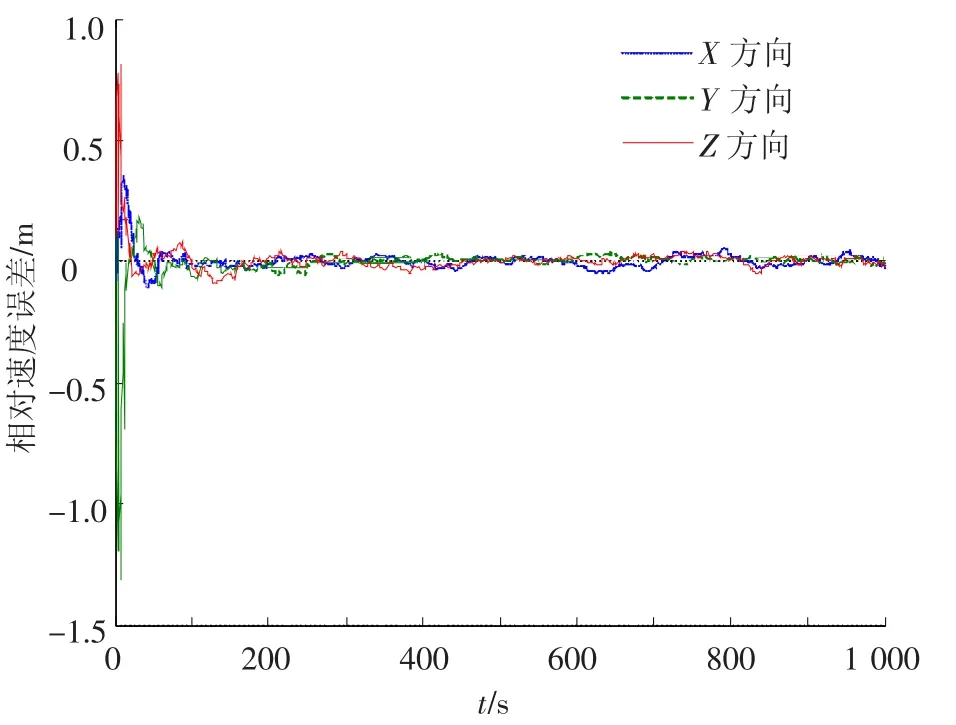
图7 三轴相对速度误差曲线

5 结论

本文对通信保障航天器的相对导航问题进行了研究，利用无线电测量技术和粒子滤波算法，设计了基于粒子滤波的通信保障航天器相对导航方法，并对提出的算法进行了仿真验证.利用本文提出的滤波算法，能够有效提高两个航天器间相对位置和相对速度的测量精度，为通信保障航天器的数据中继任务有效完成提供了有力支撑.

［1］罗建军，王明明，马卫华.在轨服务航天器导航系统仿真研究［J］.宇航学报，2010，31(2):380－385.

［2］崔乃刚，王平，郭继峰，程兴.空间在轨服务技术发展综述［J］.宇航学报，2007，28(4):805－811.

［3］刘洋，易东云，王正明.分布式小卫星SAR的基线测量方法研究［J］.飞行器控制学报，2006，25(1):26－30.

［4］马宏，王元钦，陈谷仓.编队小卫星间相对测距和时间同步方法研究［J］.装备指挥技术学院学报，2006，17(2):67－71.

［5］BATE R R.航天动力学基础［M］.吴鹤鸣，李肇杰译.北京:北京航空航天大学出版社，1990:44－127.

［6］陈谷仓，王元钦，马 宏，等.小卫星分布式雷达空间状态测量方法［J］.装备指挥技术学院学报，2005，16(4):77－80.

［7］李秋娜，袁嗣杰，刘东华.基于高级在轨系统的无线电测距方法研究［J］.计算机测量与控制，2006，14(2):172－174.

［8］陈谷仓，王元钦，王天祥，等.高精度星间基线测量方法探讨［J］.飞行器测控学报，2005，24(4):60－65.

［9］雪丹，曹喜滨，吴云华，等.基于轨道根数差的卫星编队自主定轨研究［J］.系统仿真学报，2006，18(10):2982－2955.

［10］朱志宇.粒子滤波算法及其应用［M］.北京:科学出版社，2010:12－68.

［11］Van HANDEL R.Uniform time average consistency of Monte Carlo particle filters［J］.Stochastic Processes and their Applications，2009，119(11):3835 －3861.

［12］胡士强，敬忠良.粒子滤波原理及应用［M］.北京:科学出版社，2010:14－98.

Relative navigation method of communication supporting space-craft base-on particle filter

LIU Xue-kui，SUN Zhao-wei，ZHANG Jian，DENG Hong

(1.Research Center of Satellite Technology，Harbin Institute of Technology，150001 Harbin，China)

On-orbit servicing spacecraft has become a hot research field at domestic and abroad in recent years，communication supporting spacecraft as a class of on-orbit servicing spacecraft can provide date forwarding service to the communication fault spacecraft，which can prolong the on-orbit life.In order to improve the communication supporting spacecraft antenna pointing accuracy，relative navigation algorithm of communication supporting spacecraft based-on particle filter is proposed，then more precise relative position and speed between two spacecrafts are obtained.This method takes radio equipment as the main measurement parts for its inherent characteristics，such as long measuring distance，high covering rate and all-weather work，and combines the advantage relative position and speed estimation of particle filter in nonlinear system filtering.Simulation results show that the new algorithm can effectively reduce the errors and improving relative position and speed estimation precision，ensure the space missions of communication support effectively.

particle filter;relative navigation;communication supporting;on-orbit service

V44

A

0367－6234(2012)11－0027－04

2012－02－13.

国家自然科学基金金资助项目(11002040).

刘雪奎(1964—)，男，工程师，博士研究生;

孙兆伟(1963—)，男，教授，博士生导师.

孙兆伟，sunzhaowei@vip.sina.com.

book=44,ebook=277

(编辑 苗秀芝)