与非合作目标交会的多约束有限时间最优控制

邓 泓，孙兆伟，仲惟超，陈长春

（哈尔滨工业大学卫星技术研究所，150001 哈尔滨）

与非合作目标交会的多约束有限时间最优控制

邓 泓，孙兆伟，仲惟超，陈长春

（哈尔滨工业大学卫星技术研究所，150001 哈尔滨）

针对拦截卫星的末端轨道拦截任务，研究了基于状态反馈的轨道控制器设计方法.考虑系统参数不确定性，建立了相对运动模型.同时考虑系统有限时间二次型性能指标、控制输入限幅和极点配置，提出了多约束条件的控制器设计问题并给出了控制器的设计方法.该方法采用线性不等式技术，根据Lyapunov稳定定理推导出控制器存在的充分条件，并将控制器的设计转化为一个凸优化问题进行求解.仿真结果表明，设计的控制器能够使系统稳定，并且能在获得最优系统有限时间性能的同时满足控制输入限幅和极点区域限制.

轨道控制;不确定性;有限时间性能;控制输入限幅;极点配置

拦截卫星是指根据地面指令自动接近并识别敌方卫星，以实施拦截使其失效的人造地球卫星［1］.拦截卫星通过轨道控制实现对目标卫星的逼近.近年来，随着推力器技术的发展，出现了推力可连续变化的喷气推力器.由于推力连续可变，类似于卫星姿态控制，许多控制理论可被用于轨道控制.文献［2］针对交会对接中的轨道控制问题，基于状态反馈和自适应控制理论设计了控制器，该控制器在系统存在有界干扰和测量噪声时依然有效;文献［3］提出了一种鲁棒H∞状态反馈轨道控制器设计方法，该方法通过优化系统增益抑制系统外部扰动，从而提高控制器的鲁棒性;文献［4］通过引入相平面，将Lyapunov稳定理论用于轨道交会的控制器设计，并进行稳定性分析;文献［5］将滑模控制理论用于轨道控制器的设计，与最优控制相比，采用该方法设计的控制器具有更高的精度且便于工程实现.可见，相对于传统的冲量式轨道控制［6－8］，基于控制理论的变推力轨道控制方法具有更灵活多变的形式，并可以对系统稳定性进行分析，从而达到更高的控制精度.

拦截卫星的拦截过程一般分为3个阶段:地面引导段、自动寻的阶段和最后逼近段［1］.本文主要针对拦截卫星的最后逼近段设计轨道控制器.为了快速完成拦截任务，以减少目标卫星发现并逃逸的时间，通常要求拦截卫星的拦截时间(即变轨时间)越短越好，因此可考虑采用有限时间最优控制.文献［9－10］设计的控制器不仅使航天器完成了预期的轨道变化，同时还获得了有限时间内系统状态性能指标的最优值.由于拦截卫星的机动性强，系统模型中的一些参数不可能实时精确计算.此外，由于目标卫星的非合作性和空间环境的复杂性，目标卫星的轨道角速度很难获得精确值.因此，十分有必要研究不确定系统的控制器设计方法，文献［11］和［12］分别对具有不确定参数的离散系统和连续系统设计了控制器.文献［13－14］针对推力器的推力大小有限，研究了控制输入限幅约束下的控制器设计方法.为了保证闭环系统具有一定的动态特性，文献［15］研究了极点区域约束下的控制器设计问题.

然而，这些文献在设计控制器时只考虑了其中一项或几项约束条件，很少综合考虑上述所有条件.本文提出了一种基于状态反馈的控制器设计方法，该方法不仅在保证闭环系统渐近稳定的同时优化了系统的有限时间性能，还考虑了参数不确定性、控制输入限幅和极点配置约束条件.

1 问题描述

本文的拦截卫星轨道运动是在相对参考坐标系下描述的.该坐标系的坐标原点OI为目标卫星，XI轴沿目标卫星的矢径方向，ZI轴与目标卫星轨道角动量矢量方向一致，YI与XI、ZI轴构成右手直角坐标系.假设目标卫星的轨道近似圆形，且拦截卫星相对目标卫星的距离远远小于目标卫星轨道半径，则拦截卫星相对目标卫星的轨道运动可由Hill方程描述:

式中:x、y、z为相对参考系中拦截卫星的位置分量;Fx、Fy、Fz为相对参考系下拦截卫星的轨道控制力;ω为目标卫星的轨道角速度;m为拦截卫星的质量.

令状态向量和轨道控制力向量分别为

则拦截卫星的相对轨道运动模型为

本文在设计控制器时，考虑了模型参数不确定性、系统的有限时间二次型性能指标、控制输入限幅和闭环系统极点配置多个约束条件.

1)不确定性.从式(2)可以看出，相对轨道模型的主要参数为目标卫星轨道角速度和拦截卫星的质量.然而，由于目标卫星为非合作目标，且空间环境十分复杂，很难获得精确的目标卫星轨道角速度.拦截卫星在轨道机动过程中，由燃料消耗引起的整星质量变化也不可能实时精确计算.因此，可考虑目标卫星轨道角速度和拦截卫星质量的不确定性具有如下形式:

式中:ω0、m0分别为轨道角速度和卫星质量的理论值;δ1(t)、δ2(t)为不确定度且分别满足|δ1(t)|≤1和 | δ2(t)|≤2;1、2均为不确定度幅值.

考虑上述不确定参数后，拦截卫星的相对轨道运动模型可写为

将不确定部分ΔA(t)和ΔB(t)均写成范数有界不确定形式:

2)有限时间性能指标.由于拦截卫星任务的特殊性，往往要求其能在有限时间内达到预期轨道且燃料消耗小.因此，考虑如下系统状态变量和控制变量的有限时间线性二次型性能指标，通过设计控制增益阵K，使该性能达到最小:

式中:S、Q和R均为已知的正定对称矩阵;t0和tF分别为初始时刻和终端时刻.

3)控制输入限幅.拦截卫星进行轨道机动时一般采用喷气推进器.由于推进器的推力有限，控制器的设计应满足

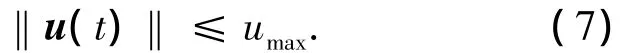
4)极点配置.由于模型的不确定性和各种扰动，精确的极点配置很难实现.若将闭环系统的极点配置在复平面上适当的区域中，可以保证系统具有一定的动态特性.本文研究的是圆盘区域约束，即闭环系统的所有极点都在圆盘区域Θ(r，q)中，其中Θ(r，q)表示复平面上半径为r，中心在(－q，0)的1个圆盘区域.

本文设计的控制器采用了状态反馈控制，其结构如下所示:

式中:K为状态反馈控制增益阵.

故闭环系统可写为

因此，本文的控制器设计问题可描述为:设计控制增益阵K，使不确定系统(9)渐近稳定且使系统有限时间二次型性能指标J达到极小值;控制输入满足式(7);闭环系统极点都在圆盘区域Θ中.

2 控制器设计

为了证明后文提出的定理，在设计控制器之前先给出几个引理.

引理1［3］设L、M和N为具有适当维数的实数矩阵且满足‖N‖≤1，则对于任意实数ε＞0，有

引理2［15］设Y、M和N为具有适当维数的矩阵，其中Y是对称阵，则对任意矩阵Γ满足ΓTΓ≤I，有Y+MΓN+NTΓTMT＜0.当且仅当存在一个常数 ε ＞0，使得Y+εMMT+ε－1NTN ＜ 0.

引理3［3］设M和N为具有适当维数的矩阵，对于任意实数ε＞0，有

引理4(Schur补引理)［16］对给定的对称矩阵

其中Y11是r×r维的，以下3个条件是等价的:

定理1 给定不确定系统(3)和状态反馈控制律(8)，如果存在正定对称矩阵P满足

则闭环系统(9)渐近稳定且性能指标(6)有上界

证明 因为Q和R均为正定阵，所以

由式(10)可得

由Lyapunov稳定定理可知，系统(9)稳定，且Lyapunov函数为V(t)=XT(t)PX(t).

将式(8)带入性能指标(6)并考虑式(10)可得

证毕.

定理2 给定不确定系统(3)和任意常数η ＞0，如果存在常数 μ ＞0、λ ＞0、α ＞0和适当维数矩阵Ω =ΩT＞0、Ψ满足

式中* 表示对称阵.则存在状态反馈控制律u(t)=KX(t)，使闭环系统(9)渐近稳定并同时满足控制输入式(7)、闭环系统极点都在圆盘区域Θ中、系统有限时间二次型性能指标有上界

且控制增益阵K可由下式计算:

证明 由定理1可知，如果不等式(10)和(11)都成立，则闭环系统(9)渐近稳定且性能指标(6)有上界.将不确定结构(4)和(5)代入式(10)可得

由引理2可得，存在常数μ＞0，使得当下式成立时，式(20)成立.

由Schur补引理可将上式写成

用 J1=diag(Ω，I，I)对式(21)做全等变换并再次利用Schur补引理，则可得到式(13).

用Ω对式(14)做全等变换得

利用Schur补引理，则式(23)等价于式(14).

可见，当式(13)和式(14)成立时，闭环系统(9)能渐近稳定且性能指标(6)有上界.

由文献［15］可知，闭环系统(9)的极点都在圆盘区域Θ(r，q)中当且仅当

用J2=diag(Ω，Ω)对式(24)做全等变换并将不确定结构代入.由引理2知，存在常数λ＞0，使得当下式成立时，则式(24)成立.

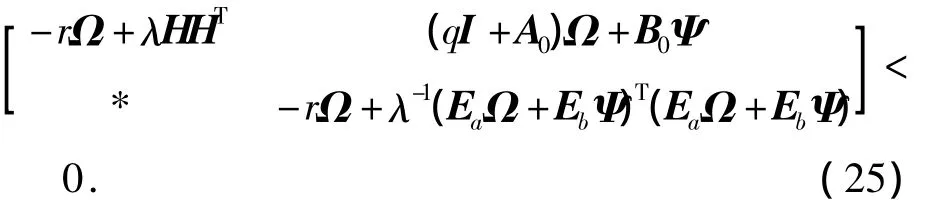
再由Schur补引理即可知，式(25)等价于式(15).即当式(15)成立时，闭环系统(9)的极点都在圆盘区域Θ(r，q)中.

由文献［17］可知，如果存在常数α＞0满足

则控制输入能满足式(7).利用Schur补引理，可知式(26)和式(16)等价.用Ω对式(27)做全等变换并根据Schur补引理可得

由引理3可知，对于任意常数η＞0，当下式成立时，式(28)一定成立:

再由Schur补引理知，上式等价于式(17).可见，当式(16)和式(17)成立时，控制输入满足式(7).

由式(12)和式(26)可知J＜α，即式(18)得证.由式(22)知，式(19)成立.证毕.

推论1 可以通过求解如下凸优化问题来设计状态反馈控制器，并获得系统有限时间二次型性能的最优值:

即对于给定的常数η＞0，寻找满足不等式(13)～(17)的常数μ＞0、λ＞0、α＞0和适当维数正定对称矩阵 S－1、Q－1、R－1、Ω 和矩阵 Ψ，使得α值最小，则由式(19)计算可得控制增益阵K.

注: 在传统的控制器设计中，通常先给定权矩阵S、Q、R.但在求解线性矩阵不等式时，给定权矩阵往往会增加解的保守性甚至无解［17］.因此，本文把权矩阵均看作变量矩阵进行求解.

3 应用实例与分析

给定η =102，利用MATLAB中的LMI工具求解推论1，可J＜α=1.832 5.

则由式(19)计算可得控制增益阵为

根据上述设计的状态反馈控制器，可仿真得到系统控制结果，如图1～5所示.图1和图2分别为相对位置和相对速度变化图.从图中可知，相对位置和相对速度均快速收敛，在500 s内分别收敛到10 m和0.1 m/s，800 s时分别为0.1 m和0.002 m/s.图3为拦截轨道示意图，可以看出，拦截卫星以近似直线的路径向目标卫星靠近，这样可以减少被发现后目标卫星的反应时间.图4为三轴控制力曲线图，可见推力均小于幅值500 N.图5给出了开环系统和闭环系统的极点位置.可见，开环系统的极点均在零点附近，而通过控制器的设计，闭环系统的极点均在左半复平面，且处于圆盘区域Θ(1，1)中.由以上仿真结果可知，所设计的控制器是有效的，且满足控制输入限幅和极点区域限制.

图1 相对参考坐标系下的相对位置

图2 相对参考坐标系下的相对速度

图3 相对参考坐标系下的拦截轨道

图4 三轴控制力输入曲线

图5 开环系统和闭环系统极点示意图

为进一步验证本文控制器设计方法对不确定系统的适用性，在仿真中，令目标卫星轨道角速度的不确定度幅值为1=0.5，拦截卫星质量的不确定度幅值为2=0.5，其它参数不变.结果表明，相对位置和相对速度依然快速收敛并稳定，500 s内仍可分别收敛到10 m和0.1 m/s，800 s时控制精度分别为0.1 m和0.002 m/s.这说明设计的控制器是有效的，并且对系统的不确定部分具有较好的鲁棒性.

为说明参数不确定性对闭环系统性能的影响，在本文控制器设计时不考虑参数的不确定性，且在其他约束条件和仿真条件不变的情况下，可计算控制增益阵为

在该控制器下，相对位置和相对速度的仿真结果如图6和图7所示，其动态收敛过程的性能差于图1和图2，且800 s时控制精度分别为1.7 m和0.03 m/s.可见，若不考虑参数不确定性，将会影响闭环系统的动态特性且控制精度底，从而说明了本文算法对参数不确定系统的有效性.

图6 不考虑参数不确定性时的相对位置

图7 不考虑参数不确定性时的相对速度

4 结论

1)本文针对拦截卫星的轨道拦截任务，考虑了多约束条件和系统有限时间二次型性能指标的优化，提出了一种基于LMI的轨道控制器设计方法.仿真结果表明，在系统模型存在不确定参数时，本文设计的控制器能够使系统稳定，并且能在获得最优系统有限时间性能的同时满足控制输入限幅和极点区域限制.由于本文设计的控制器采用的是状态反馈控制，其结构简单，因而便于工程应用.

2)本文对系统的有限时间二次型性能指标进行了优化.但由于拦截卫星任务的特殊性，需要进一步研究系统在有限时间内的稳定问题.因此，下一步的工作是基于LMI方法设计控制器，使系统在有限时间稳定并满足多约束条件.

［1］周克强，高晓光，白奕.反卫星卫星攻击方式研究［J］.飞行力学，2006，24(4):80－83.

［2］SINGLA P，SUBBARAO K，JUNKINS J L.Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty［J］.Journal of Guidance，Control，and Dynamics，2006，29(4):892 －902.

［3］GAO Huijun，YANG Xuebo，SHI Peng.Multi-objective robust H∞control of spacecraft rendezvous［J］.IEEE Transactions on Control Systems Technology，2009，17(4):794－802.

［4］TIWARI A，FUNG J，CARSON J M，et al.A framework for Lyapunov certificates for multi-vehicle rendezvous problems［C］//Proceedings of American Control Conference.Boston:［s.n.］，2004:5582 －5587.

［5］EBRAHIMI B，BAHRAMI M，ROSHANIAN J.Optimal sliding-mode guidance with terminal velocity constraint for fixed-interval propulsive maneuvers［J］.Acta Astronautica，2008，60(10):556－562.

［6］佘志坤，薛白，丛源良，等.最优双冲量交会问题的数学建模与数值求解［J］.宇航学报，2010，31(1):155－161.

［7］TEBBANI S，ISABELLE Q，JACQUES B.Optimal finite thrust rendezvous using beneficial effects of the earth oblateness［J］.Astronautical Sciences，2002，109:2497－2508.

［8］GOODSON T，CHUANG J C H，HANSON J.Optimal finite thrust orbit transfers with large numbers of burns［J］.Journal of Guidance，Control，and Dynamics，1999，22(1):139－148.

［9］刘丽丽，文浩，金栋平，等.绳系卫星轨道转移的最优控制［J］.航空学报，2009，30(2):332－336.

［10］李四平，刘锦阳，国凤林，等.轨道机动的时间能量综合最优控制［J］.宇航学报，2010，31(1):137－142.

［11］沈毅，刘皓.基于时滞不确定理论的导弹鲁棒控制系统设计［J］.航空学报，2011，32(3):473－479.

［12］PENG S，BOUKAS E K.On H∞control design for singular continuous-time delay systems with parametric uncertainties［J］.Journal of Nonlinear Dynamics and Systems Theory，2004，4(1):59－71.

［13］YUE Xincheng，YANG Ying，GENG Zhiyong.Indirect optimization for finite-thrust time-optimal orbital maneuver［J］.Journal of Guidance，Control and Dynamics，2010，33(2):628－634.

［14］涂良辉，袁建平，罗建军.基于伪光谱方法的有限推力轨道转移优化设计［J］.宇航学报，2008，29(4):1189－1193.

［15］YANG Xuebo，BO Yuming，LIU Yurong，et al.Output tracking control for autonomous spacecraft rendezvous［C］//IEEE Conference on Decision and Control.Piscatawary:IEEE，2009:5227－5232.

［16］俞立.鲁棒控制——线性矩阵不等式［M］.北京:清华大学出版社，2002:8－9.

［17］YANG Xuebo，GAO Huijun，SHI Peng.Robust orbital transfer for low earth orbit spacecraft with small-thrust［J］.Journal of the Franklin Institute，2010，347(10):1863－1887.

Finite time optimal control for non-cooperative targets rendezvous with multi-constraints

DENG Hong，SUN Zhao-wei，ZHONG Wei-chao，CHEN Chang-chun

(Research Center of Satellite Technology，Harbin Institute of Technology，150001 Harbin，China)

This paper studies the problem of orbit control for intercepting satellite based on state feedback control considering parametric uncertainties，finite time performance，control input constraint and poles assignment.The sufficient condition of controller is derived by Lyapunov approach，and then the controller design is transformed into a convex optimization problem in terms of linear matrix inequality.An illustrative example shows that the system is asymptotically stable with the designed controller and the optimal performance is obtained with control input and poles assignment constraints.

orbit control;uncertainty;finite time performance;control input constraint;poles assignment

V448.234

A

0367－6234(2012)11－0020－07

2011－10－09.

邓 泓(1986—)，女，博士研究生;

孙兆伟(1963—)，男，教授，博士生导师.

邓 泓，denghong@yeah.net.

(编辑 张 宏)