机动发射的弹道导弹飞行诸元的快速计算

韦文书，荆武兴，高长生

（哈尔滨工业大学航天工程系，150001 哈尔滨）

式中:φ为地表一点的地心纬度;B为该点的地理纬度;a、b分别为地球的长半轴和短半轴.

O、T两点地心角和球面方位角能够通过球面三角关系得到:

机动发射的弹道导弹飞行诸元的快速计算

韦文书，荆武兴，高长生

（哈尔滨工业大学航天工程系，150001 哈尔滨）

基于解析预报与数值寻优相结合的方法，本文研究机动发射的弹道导弹飞行诸元快速设计问题.首先，利用线性回归方法建立了导弹诸参数与发射信息之间的多项式拟合关系式，利用该式可以得到飞行方案诸参数迭代初值;然后，以弹道落点纵向偏差、横向偏差及弹道顶点高度偏差平方和极小为指标函数，采用Levenberg-Marquardt方法搜索诸参数精确解;最后，以民兵III弹道导弹为例，对所提方法进行了仿真验证，研究结果表明，该方法计算量少，适合已定参数的导弹大范围机动发射的快速计算，且在落点精度要求不高的情况下，可以用解析表达式的解作为弹道飞行方案诸元的值，对目标进行打击.

解析预报;机动发射;Levenberg-Marquardt方法;多级弹道导弹;线性回归方法

导弹飞行方案设计的目的是找到满足所有系统要求的最适合的弹道［1］.对于机动发射的弹道导弹来说，针对不同的发射点和目标点等攻击信息能够快速选取飞行方案诸参数，将大大的提高导弹的作战效能.所以，机动发射弹道导弹的飞行方案快速设计是1个重要的、亟待解决的内容.目前，飞行方案设计包括直接法、间接法和智能优化算法等［2－8］，然而这些方法通常需要大量的计算［9］，故对于机动发射的弹道导弹来说不能够迅速计算其弹道诸参数.

描述飞行器空间弹道的方法有3类:解析法、数值积分和函数逼近法.解析法计算速度快，实时性好，但解析解求取困难且精度受限;数值积分法精度高，缺点是计算复杂，实时性好;函数逼近法介于解析法和数值积分法之间.目前，国内外有很多学者致力于函数逼近法的研究［10－13］.如陆平［14］在研究多级火箭上升段制导方案过程中，将飞行高度拟合成1个多项式，从而设计了二级火箭的反馈控制律.

王明海［15］等将落地射程偏差和方位角偏差的二元迭代分解成两个一元迭代，从而提供了弹道导弹弹道设计的一种快速迭代方法，该方法对多变量、有约束的弹道设计有一定缺陷;黄岳［16］等以发射方位角为射击诸元，对球面方位角迭代得到发射方位角，该方法计算时间较长，不适合机动发射的弹道导弹弹道设计;刘刚、何麟书等［17］基于微积分、变分原理提出一种多级火箭飞行方案设计的工程方法，该方法考虑工程约束较少.

本文研究机动平台发射的三级固体弹道导弹全弹道飞行方案设计，不同的发射点纬度、射向、射程对应不同的飞行方案弹道，弹道诸元的快速选取对导弹的效能有重大影响.为了减少大量计算，本文将解析预报与优化方法相结合，能够快速给出最优的期望方案.首先，对弹道进行分段，根据每段的飞行特性，设定了相应的约束条件，设计了飞行方案;其次，通过开环仿真得到了飞行方案诸元与发射点、目标点等信息的数据库，利用多项式拟合他们之间的解析关系式，从而，对一定打击范围内任意的发射点、目标点及期望弹道顶点高度，能够迅速给出飞行方案诸元的近似值;然后，以解析表达式得到的近似值为初值，纵向、横向、及高度偏差的平方和极小为目标函数，采用L-M法进行迭代计算，得到诸元的精确值;最后，对文中方法进行了仿真，结果表明:采用解析预报能快速给出诸元概略值，以此为初值，采用数值方法只需少量计算即可得到精确值;当落点精度要求不高时，可以用解析预报的值直接作为诸元的真值来打击目标.

1 数学模型

弹道导弹运动模型基于六自由度弹道仿真模型建立.考虑地球自转、标准椭球模型，不考虑级间分离干扰误差，给定发射方位角与主动段飞行程序角后，导弹即可按预定弹道飞行.

发射坐标系［18］中导弹的数学模型为

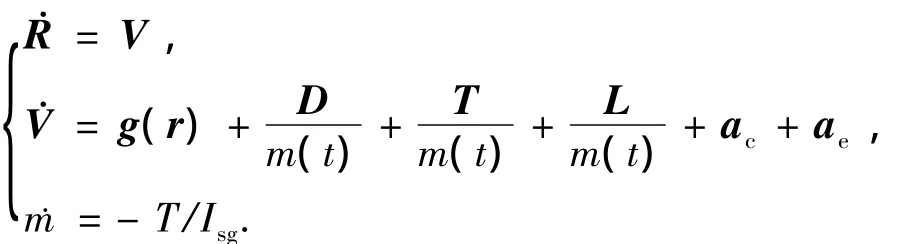
其中:R为导弹相对发射系的位置;V是导弹相对发射系的速度;T为推力;m为t时刻质量;D为气动阻力;L为气动总升力，T为推力幅值;Isg为比冲;ac为科氏加速度;ae为牵连加速度.

引力加速度的表达式是

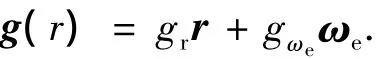
其中:r为地心到飞行器的矢量;ωe为地球自转角速度矢量，则

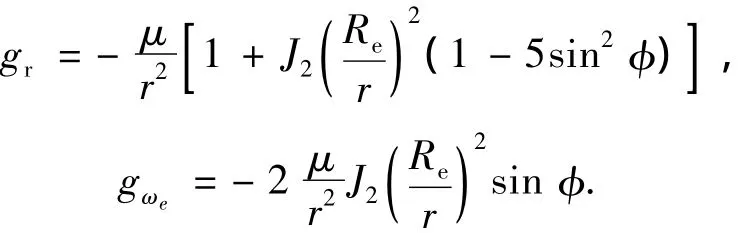
式中:r为地心到飞行器的距离;μ为地球引力常数;Re为地球赤道平均半径;J2为带谐系数;φ为地心纬度.

科氏加速度的表达式为

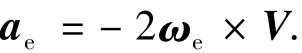
牵连加速度的表达式为

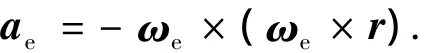
弹道导弹一般是轴对称的，定义其体坐标系为obxbybzb.由气动力的定义可以得到，气动阻力和气动总升力为

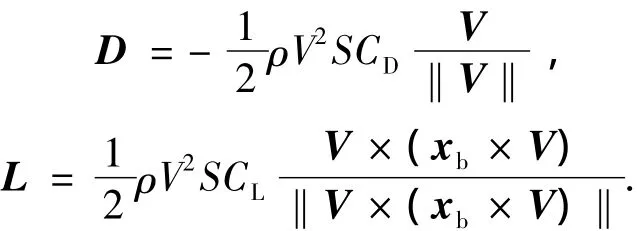
式中CD、CL分别为阻力系数和总升力系数，它们均为攻角α和马赫数Ma的函数.

发动机的推力矢量沿着obxb轴方向，利用发射坐标系到体坐标系的转换矩阵A，可得到推力在发射坐标系中的投影，其中

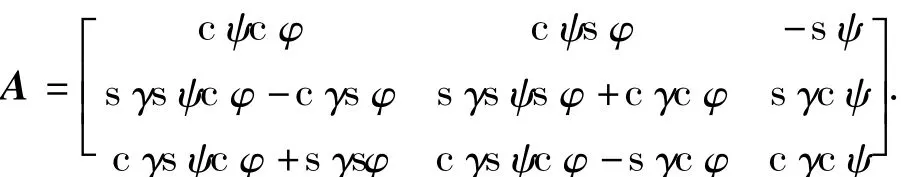
式中:s代表 sin;c代表 cos;γ、φ、ψ分别为滚转角、偏航角、俯仰角.

2 工程描述

对于多级固体弹道导弹，其主动段飞行方案有3种模式:连续推力模式、连续推力+滑行(小推力末端修正)、间隔推力模式.本文选取连续推力模式.

飞行程序通常指的是主动段飞行时程序角的变化规律.其选择原则为:

1)垂直飞行段，要确定转弯时刻，其选取比较灵活，一般不能小于由发射条件所确定的规定时间;

2)跨音速段的攻角应接近零值，这样可减小气动特性剧烈变化而造成的影响;

3)导弹飞过跨音速，进入高动压区，应考虑壳体温度和载荷的限制，为了使导弹较轻，又不至于造成折断的危险，需要限制攻角;

4)程序要简单易行，引入瞄准段，即此段内程序角为常值，这样，导弹就可以在规定的各种射程内使用;

5)级间分离时，应尽量保证可靠分离和有利于下一级起控.因此，程序选择时，适当提高第一级分离高度，并在第一级发动机关机前后的瞬间采用零攻角飞行程序;

6)飞行程序要考虑头部再入大气层的限制，如动压、再入点弹道倾角等.

综合以上原则，三级导弹的主动段飞行方案为

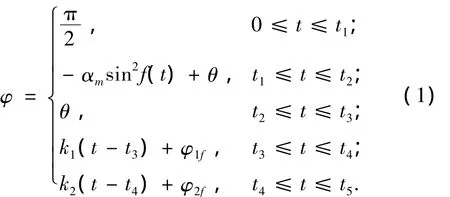
其中:t1为转弯开始时刻;t2为重力转弯开始时刻;t3为一级关机时刻;t4为二级关机时刻;t5为三级关机时刻;φ1f为一级关机时刻俯仰角;φ2f为二级关机时刻俯仰角;θ为弹道倾角;k1为二级俯仰角变化率;k2为三级俯仰角变化率;

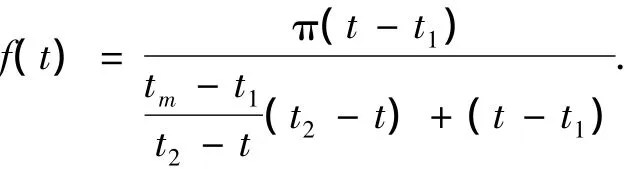
式中tm为攻角绝对值等于极值的时刻.

3 计算方法

3.1 诸元解析预报

发射方位角是弹道导弹的重要射击诸元，通常根据发射点和目标点的位置信息，以球面方位角为初值，进行迭代搜索发射方位角.本文用球面方位角确定发射坐标系，选取偏航角来修正弹道，克服地球旋转带来的横向偏差.

对于参数已定的多级导弹，采用文中的数学模型和飞行方案，选取不同的发射点地理纬度B0、球面方位角A0、转弯段最大负攻角绝对值αm、二级等俯仰角速率k1，三级等俯仰角速率k2，常值偏航角ψ等物理量，进行开环仿真计算，得到对应的弹道顶点高度H与射程角β.挑选满足约束条件的弹道并存储相应的诸元参数于数据库中，利用线性回归技术得到攻击信息与诸元之间的关系式.机动发射情况下，能够利用解析关系式迅速获得满足约束的诸元近似值.通过研究诸元与H、β的关系，发现用二次多项式拟合各参数之间的关系能够达到较理想结果.

本文以民兵三导弹为例，其具体参数见表1.

表1 民兵3导弹参数

以式(1)及如下的式(2)～式(4)为约束条件，按照下列方式建立数据库:球面方位角、纬度间隔选取10°;转弯段负攻角极值间隔选取1°;二、三级俯仰角变化率间隔选取0.005.对数据进行处理可以得到:

分析以上各式，不难发现:诸元与发射点、目标点的位置没有直接关系，只与发射点地理纬度、发射点和目标点之间的射程、发射方位角有关.因此，以上解析表达式能够使民兵三导弹大范围内机动快速发射，或者快速打击射程范围内的任意目标.对于其他机动发射的弹道导弹，可以采用本方法，建立数据库，然后利用线性回归技术处理数据库数据，得到诸元与攻击信息之间的表达式，在变点发射时，能够快速获得诸元概略值.

3.2 诸元数值寻优

当发射点为O(λo，Bo)、目标点为T(λT，BT)，发射点、目标点的地心纬度可用下式计算:

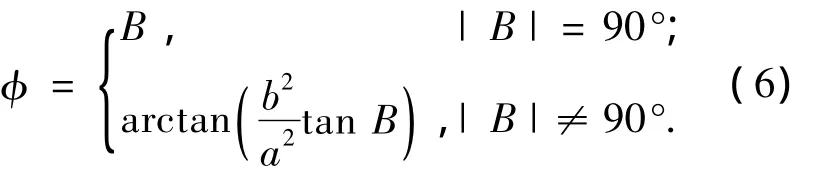
式中:φ为地表一点的地心纬度;B为该点的地理纬度;a、b分别为地球的长半轴和短半轴.

O、T两点地心角和球面方位角能够通过球面三角关系得到:

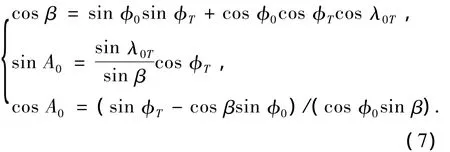
因为远程弹道导弹的射程不超过20 000 km，所以β在I、II象限内取值，A0在4个象限内取值，故β、A0的计算公式为

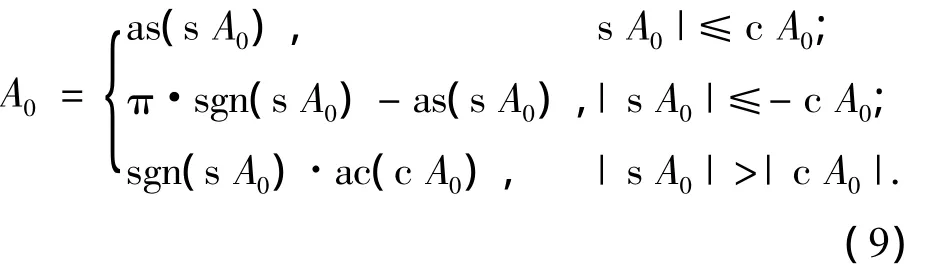
式中:sgn为符号函数;as代表 arcsin;ac代表arccos.

设定期望的弹道高度，利用式(6)～(12)可得一组初值，然后选取参数X=［αmk1k2ψ］T为变量，以

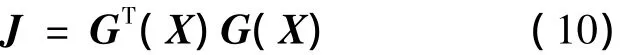
的值等于零为目标函数.最终以数值方法对参数寻优.式中 G(X)= ［ΔL Δz ΔH］T.ΔL为纵向偏差;Δz为横向偏差，即r在oz轴投影;ΔH弹道高度与期望高度偏差.

由解非线性最小二乘问题的L-M方法可得到［19］:

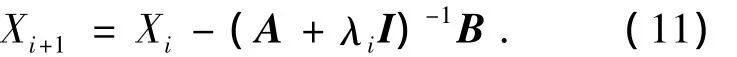
其中:i=0，1，…;I为4阶单位阵;λi为加权系数，且0 ＜ λi＜1.

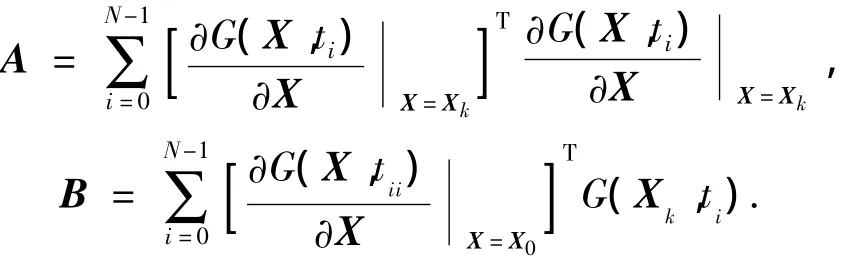
全局收敛的L-M方法计算步骤如下:

步骤1 取 ρ，σ ∈ (0，1)和 λi＞ 0，X0∈R4×n，置 i=0;

步骤2 若G(Xi)=0，停止计算;

步骤3 求解方程组(A+λiI)di=－B得到di;

步骤4 由Armijo搜索求步长，令τi是满足下面不等式的最小非负整数τ:

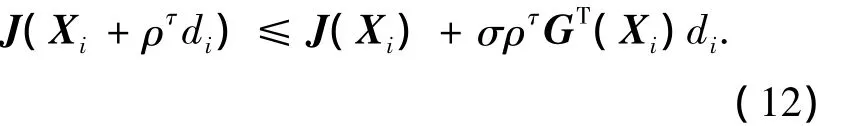
令 τI= ρτ，置 Xi+1=Xi+ εidi+1，i=i+1.

步骤5 目标函数的最优值为0，可以按式λi= ‖G(Xi)‖1+σ，σ ∈［0，1］更新 λk的值，转步骤2.

4 仿真分析

4.1 仿真条件

以民兵三导弹为例，选择三级固体弹道导弹，其起飞重量为34 500，弹长为18.26 m，其他重要参数如表1所示.

4.2 仿真结果及分析

设置四组仿真场景，其中发射点O和目标点T，发射点和目标点高程Ho、HT，期望弹道顶点高度H.利用多项式逼近的结果、以多项式结果为初值，式(10)为性能指标，利用如表2所示的攻击参数进行L-M迭代，结果如表3所示.

表2 攻击参数列表

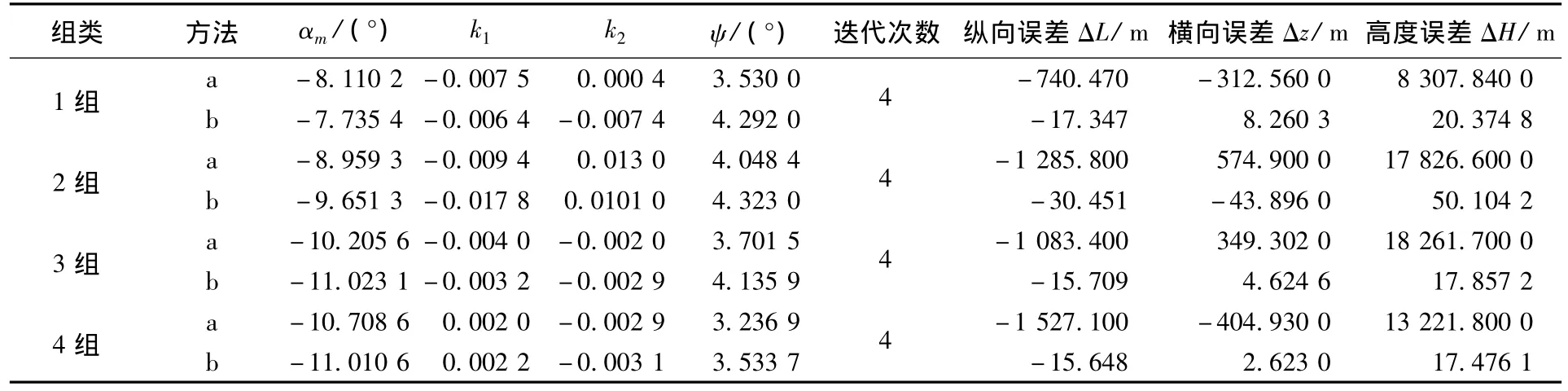
表3 不同特征分类结果比较

由表2可知，第一组和第二组为相同发射点攻击不同目标，第二组和第三组是不同发射点攻击相同目标，第三组和第四组是相同发射点、相同目标点、不同飞行高度，第一组和第三组为不同发射点、不同目标点.

对比表3的结果，文中方法能够解决导弹机动发射情况下弹道诸元快速计算问题.如果在不追求精度的情况下，可以采用本文的拟合函数进行计算，得到的解析表达式能够使落点达到精度5 km以内;若希望得到精确的弹道参数，则可以拟合公式的解为初值，利用L-M方法进行4～6次迭代计算即可.

以第一组场景为例，给出本文方法得到的仿真曲线，如图1～图2所示.由图1可知，导弹能够准确击中目标;由图2可知，弹道顶点高度与期望高度一致.

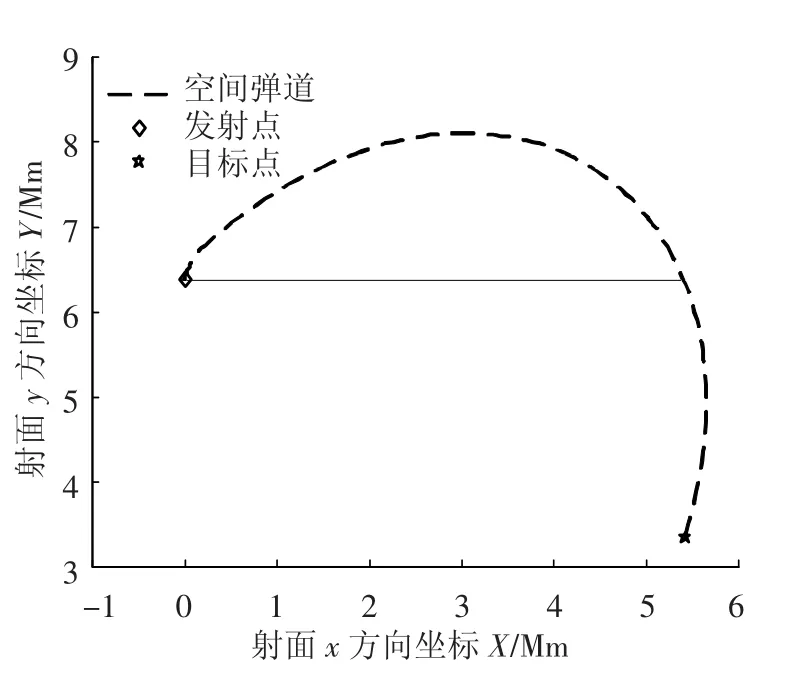
图1 纵向射面内曲线

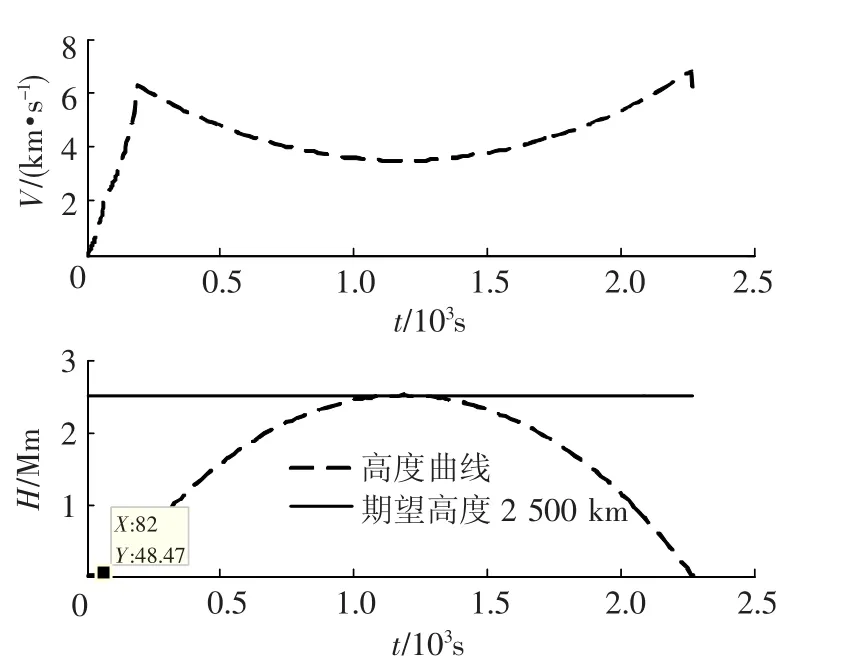
图2 速度和高度曲线

5 结论

本文基于解析预报与参数优化，对三级固体弹道导弹飞行方案的诸元进行了快速设计.利用多项式函数拟合了诸元与弹道的方位角、纬度、弹道顶点高度、射程等参数的函数关系;对于任意的发射点、目标点和期望的顶点高度，利用这个函数关系可以迅速得到诸元的近似值;以弹道诸元为变量，以纵向偏差、横向偏差、及顶点高度偏差的平方和极小为指标，用L-M方法可以得到诸元的精确值，文中将近似值、L-M方法的解进行了对比分析.本文的结论如下:

1)用多项式对弹道参数和导弹攻击参数进行拟合，能够得到近似解，在落点精度要求不高的情况下，可以用此解直接作为弹道飞行方案诸元的值，从而实现机动平台发射的三级弹道导弹飞行方案参数快速选取.

2)多项式拟合的方法，即函数逼近的方法，大量应用于弹道落点预测问题，本文以逼近函数的解为初值，利用L-M方法迭代寻优，节省大量计算，适合快速计算.

3)本文虽然是针对三级固体弹道导弹进行研究，但本文的方法具有通用性，适合多级固体或液体弹道导弹飞行方案设计.

［1］ROH W R，KIM Y.Trajectory optimization for multistage launch vehicle using time FEM versus collocation［R］.Reston VA:AIAA，1999:AIAA－99－4072.

［2］LU P，PAN B F.Highly constrained optimal launch ascent guidance［J］.Journal of Guidance，Control，and Dynamics.2010，33(2):404 －414.

［3］DUKEMAN G A.Atmospheric ascent guidance for rocket-powered launch vehicles［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Monterey:［s.n.］，2002:AIAA 2002 －4559.

［4］LEUNG M S K，CALISE A J.Hybrid approach to nearoptimal launch vehicle guidance［J］.Journal of Guidance，Control，and Dyanmics，1994，17(5):881 －888.

［5］GATH P F，CALISE A J.Optimization of launch vehicle ascent trajectories with path constraints and coast arcs［J］.Journal of Guidance，Control and Dynamics，2001，24(2):296 －304.

［6］CHRISTOPHER L D，WILLIAM W H，ANIL V R.Direct trajectory optimization using a variable low-order adaptive pseudospectral method［J］.Journal of Spacecraft and Rockets，2011，48(3):433 －444.

［7］LISA S，MARC M.General adaptive guidance using nonlinear programming constraint-solving methods［J］.Journal of Guidance，Control，and Dynamics，1993，16(3):517－522.

［8］PARK S Y.Launch vehicle trajectories with a dynamic pressure constraint［J］.Journal of Spacecraft and Rockets，1998，35(6):765 －773.

［9］JOHN T B.Survey of numerical methods for trajectory optimization［J］.Journal of Guidance，Control，and Dynamics，1998，21(2):193 －203.

［10］OLIVER M，MARKUS M.GPS based prediction of the instantaneous impact point for sounding rockets［J］.Aerospace Science and Technology，2002，(6):283 －294.

［11］LI Y C，KIRUBARAJAN T.Trajectory and launch point estimation for ballistic missiles from boost phase LOS measurements［C］//1999 IEEE Aerospace Conference，Aspen，CO，Proceedings.Piscataway:IEEE，1999:425－442.

［12］BENSON A，THORVALDSEN T，RAO Y.Direct trajectory optimization and costate estimation via an orthtogonal collocation method［J］.Journal of Guidance，Control and Dynamics，2006，29(6):1435 －1440.

［13］ROSS I M，FAHROO F.Legendre pseudo-spectral approximations of optimal control problems［C］//Lecture Notes in Control and Information Sciences.Berlin:［s.n.］，2003，295:C101 － C115.

［14］LU P.Trajectory optimization and guidance for an advanced launch system［C］//30th Aerospace Sciences Meeting ＆ Exhibit.Reno，NV:［s.n.］，1992:1 －6.

［15］王明海，李邦杰.弹道导弹弹道设计的一种快速迭代方法［J］.飞行力学，2007，25(2):75 －77.

［16］黄岳，肖凡，张涛.弹道导弹发射方位角快速计算新方法［J］.四川兵工学报，2009，30(6):51 －52.

［17］刘刚，MURAD Y，何麟书.一种多级火箭飞行方案设计的工程方法［J］.航空学报，2005，26(1):50－53.

［18］贾沛然，陈克俊，何力.远程火箭弹道学［M］.长沙:国防科技大学出版社，1993:7－8.

［19］马昌凤.最优化方法及其 Matlab程序设计［M］.北京:科学出版社，2010:87 －96.

A rapid method for flight program design of the ballistic missile launched on mobile platform

WEI Wen-shu，JING Wu-xing，GAO Chang-sheng

(Dept.of Aerospace Engineering，Harbin Institute of Technology，150001 Harbin，China)

Combining analytical prediction and optimization of parameters，a rapid method for basic firing data of flight program of the ballistic missile launched on mobile platform is studied.First，the analytical expressions between the parameters about flight program and attack information are obtained by using polynomial function approximation，by which the initial value of the firing data can be calculated.Second，considering the parameters of flight program as variables and the least square of the placement＇s aberration as the performance index，the Levenberg-Marquardt(L-M)Method is used to obtain the optimal values.Finally，as an example，the proposed method is provided to attacking targets with the LMG-30G.The simulation results show that，because of the less computational effort，the proposed method is suitable for the rapid design of the Big Wide Intratheater Mobility for the missile.When the precision of the placement is not highly demanded，the solution of analytical expressions can be used directly as the value of flight parameters to attack the target.

analytical prediction;launched on mobile platform;Levenberg-Marquardt method;the multi-stage ballistic missile;polynomial function approximation

V412

A

0367－6234(2012)11－0007－06

2011－12－05.

国家自然科学基金资助项目(11172077).

韦文书(1987—)，男，博士研究生;

荆武兴(1965—)，男，教授，博士生导师.

韦文书，weiwenshu11@hotmail.com.

(编辑 张 宏)