不确定时滞系统的控制器设计

孙凤琪

（东北大学系统科学研究所，110819 沈阳）

考虑下面不确定时变时滞系统:

不确定时滞系统的控制器设计

孙凤琪

（东北大学系统科学研究所，110819 沈阳）

为了消除时滞和不确定性给实际系统造成的不良影响，采用鲁棒控制系统设计技术，进行鲁棒控制，对具有不确定性的系统，设计1个反馈增益控制器，使系统在不确定性的容许变化范围内满足设计要求，降低系统的灵敏度.通过构造一种新的Lyapunov泛函方法，研究了一类带有时变时滞的不确定系统的鲁棒控制问题.通过细化不确定信息的结构，给出了基于线性矩阵不等式的控制器设计方法.

Schur补引理;状态反馈控制;不确定时滞系统

1 几个引理［1］

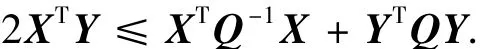
其中Q ＞0对称正定矩阵.特别地，当Q=ε时，有下面矩阵不等式:

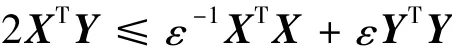
成立.

引理2 已知矩阵E、D和对称矩阵Y，对任意的不确定矩阵F(t)，如果满足如下矩阵不等式:

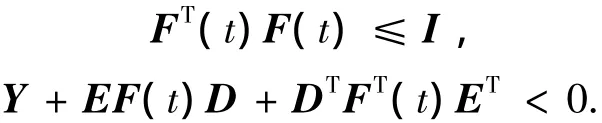
则当且仅当存在η＞0，使得

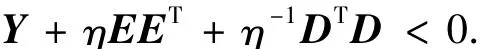
2 主要结论

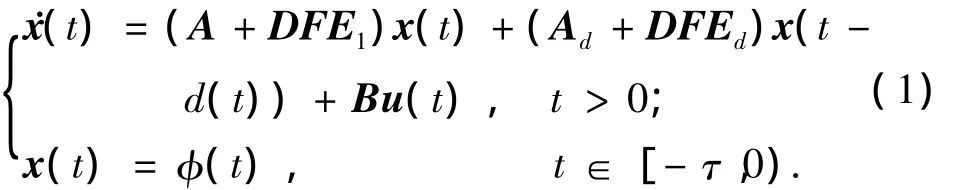
考虑下面不确定时变时滞系统:

其中:x(t)∈Rn是系统状态向量;u(t)∈Rm是输入向量;A、Ad、B是已知的适当维数的定常矩阵，A渐进稳定.d(t)是时滞可微函数，并且满足下式:

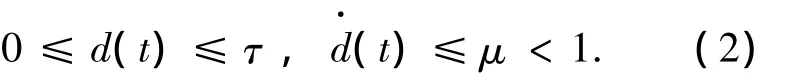
式中:τ，t是已知常数，φ(t)是连续向量初始函数.D、E1、Ed是已知的适当维数定常矩阵，表示不确定性结构信息［2］，F(t)∈ Ri×j是范数有界的不确定系统模型参数矩阵，其满足

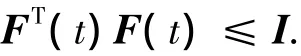
假设系统状态可测，设

那日本兵又骂一声八嘎，准备再给周教授两耳光。鬼子军官挥手制止了。鬼子军官背着手沿周教授走了一圈儿，又沿五个人走了一圈儿，最后面对着几个站定，用生硬的中国话说，你们的，什么的干活？

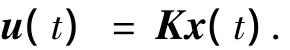
其中K是适当维数待定控制增益矩阵，则闭环系统成为

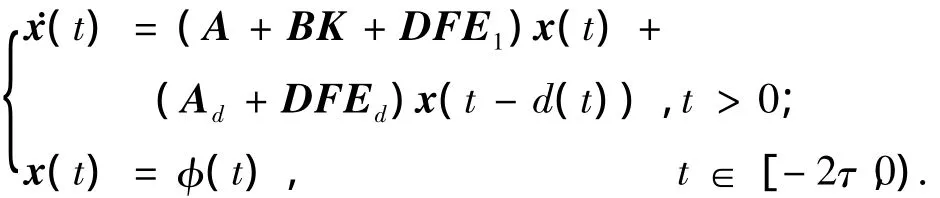
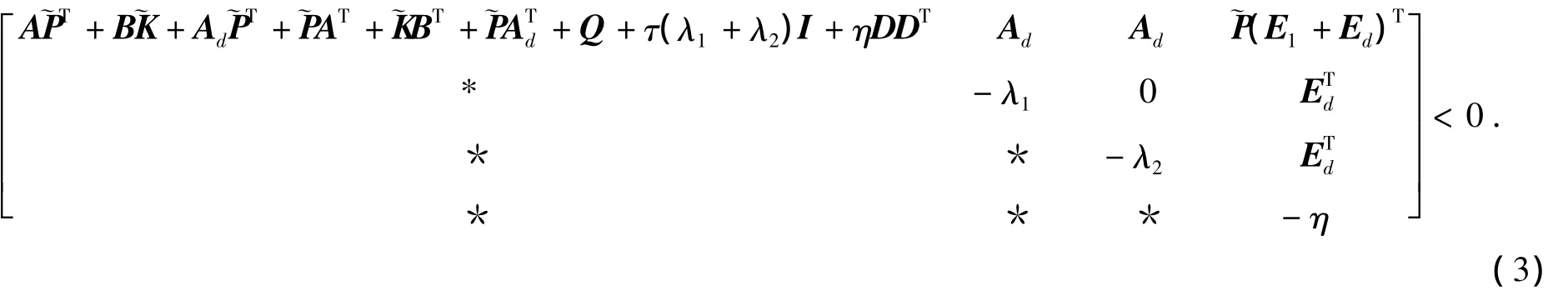
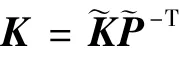
证明 由下式

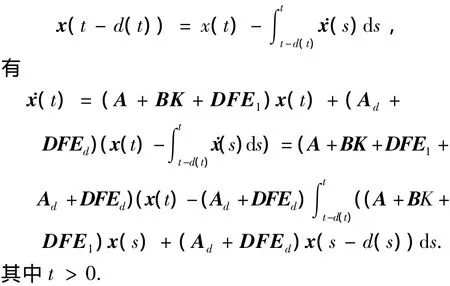
定义Lyapunov-Krasovskii泛函如下:

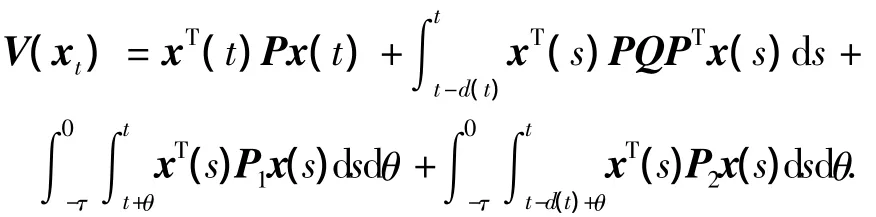
其中P ＞0，Q ＞0，P1＞0，P2＞0是适当维数正定加权矩阵，这样V(xt)就是正定的Lyapunov-Krasovskii泛函.

把V(xt)沿着系统(1)的轨迹进行微分，得

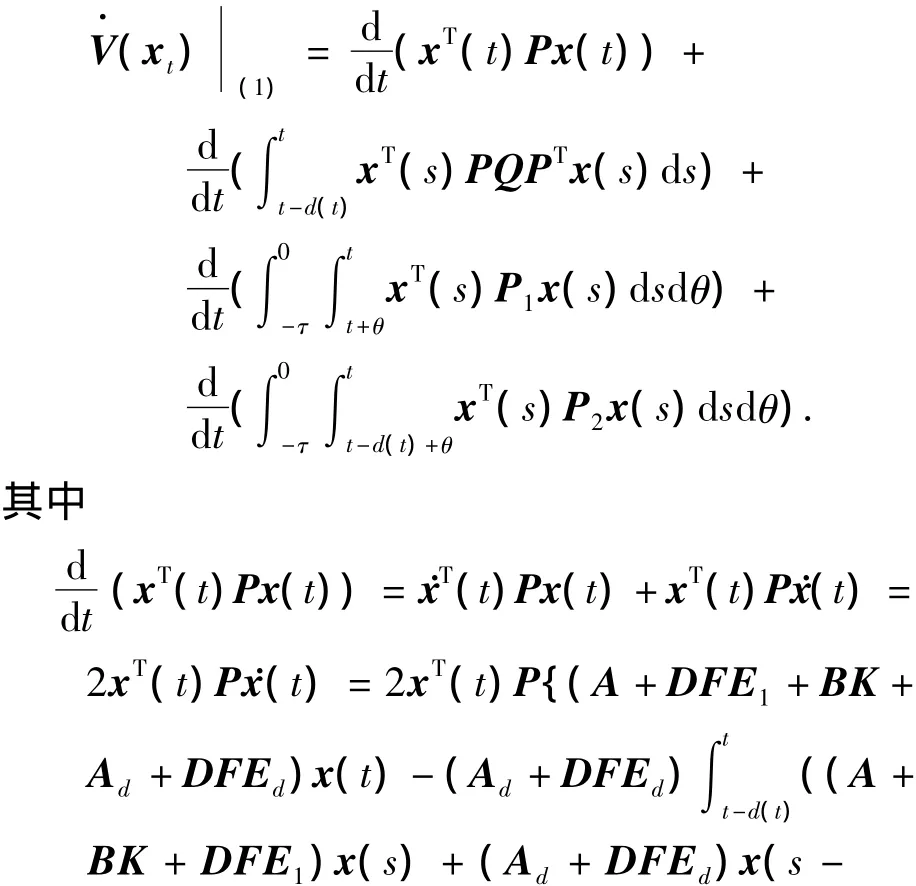
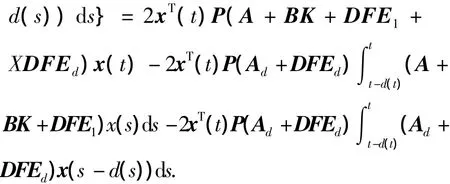
由引理1知，存在常量λ1＞0，λ2＞0，经推导整理，得下式:

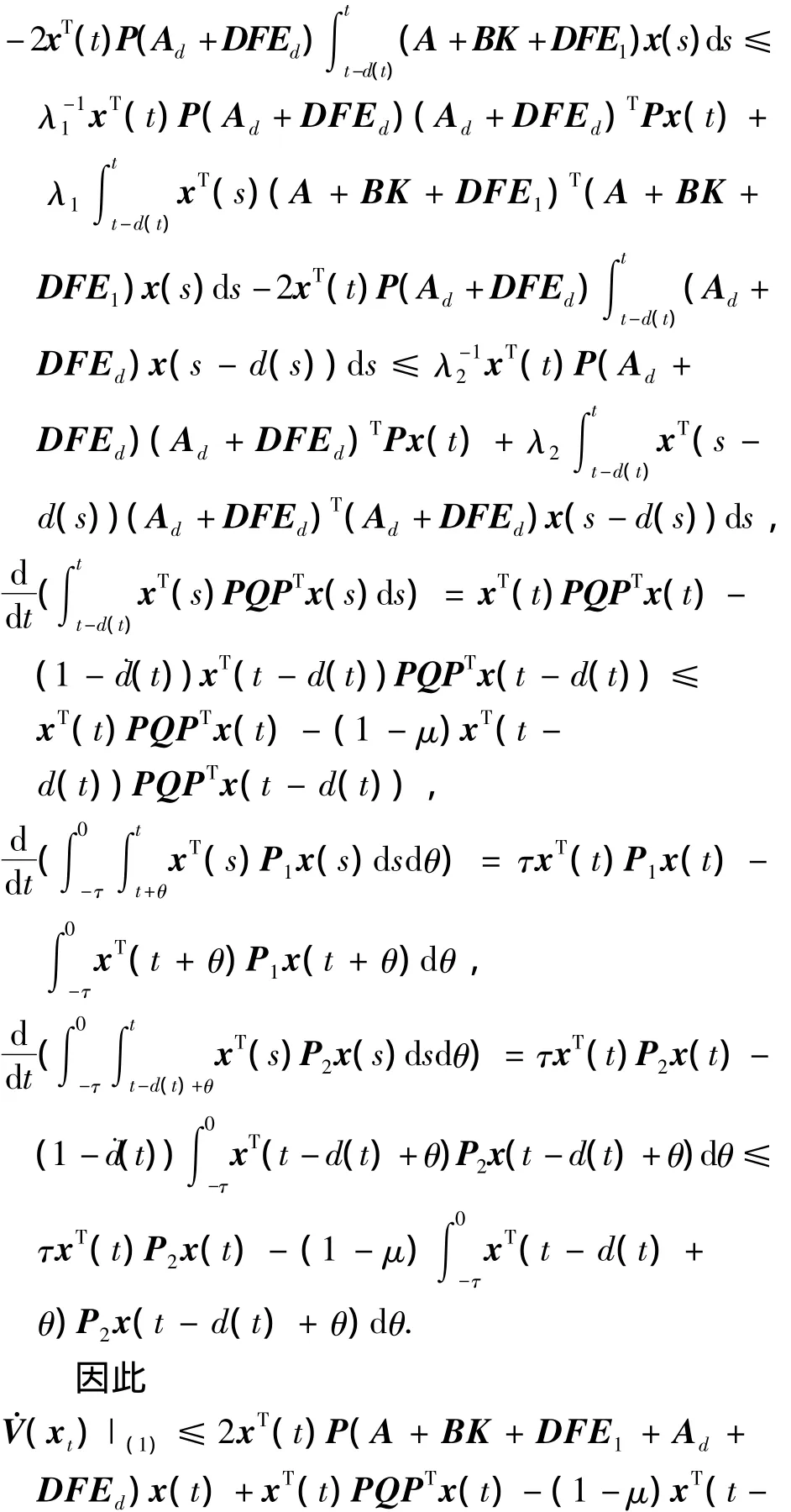
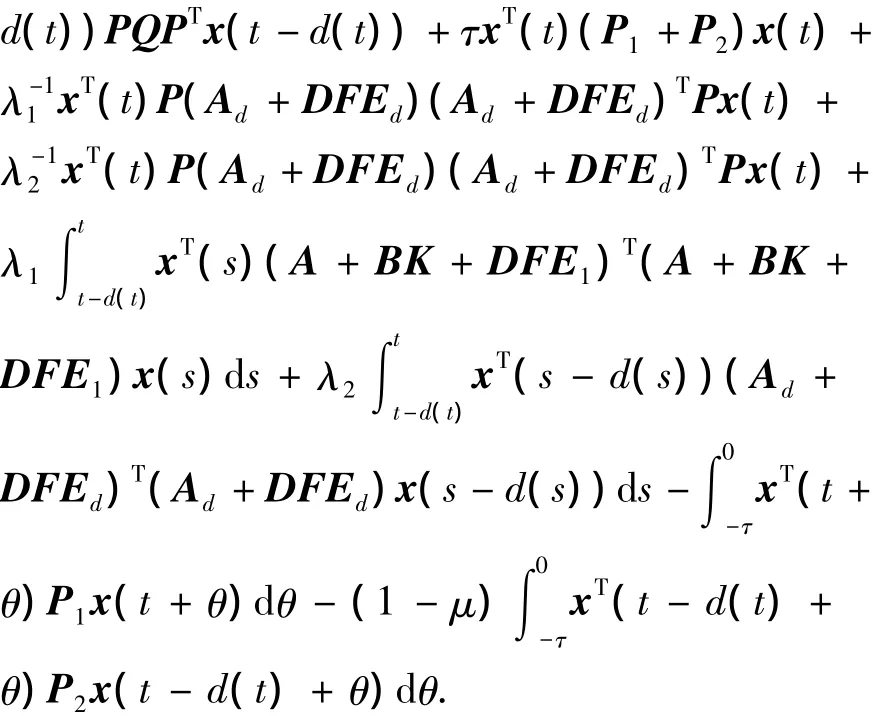
由文献［3］，存在 α ＞0，β ＞0

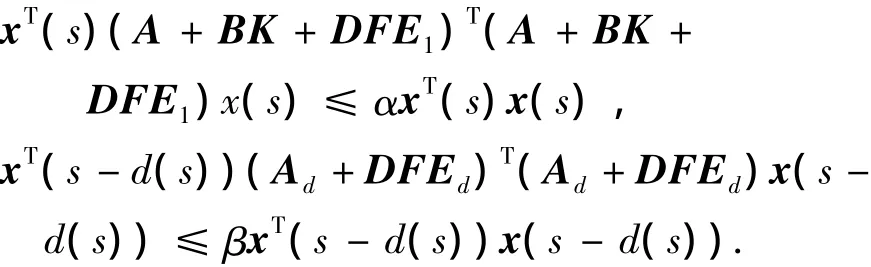
再用文献［4］类似的方法，得

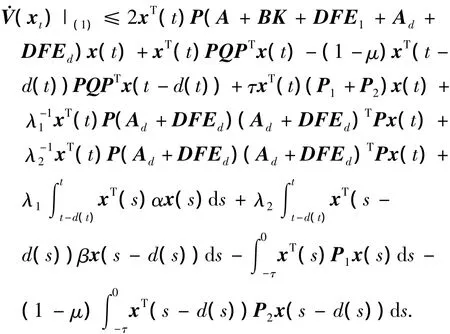
又由式(2)得

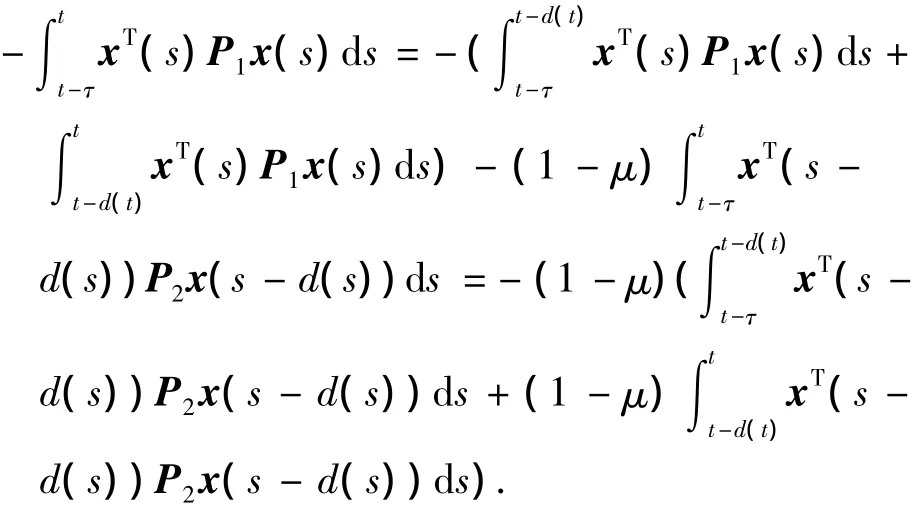
取 P1= λ1αI，P2= λ2βI，则整理得

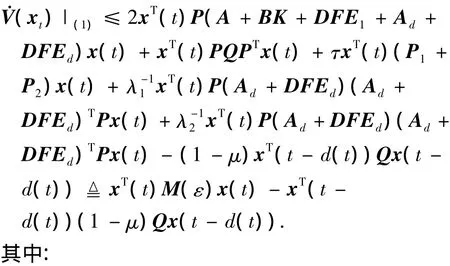
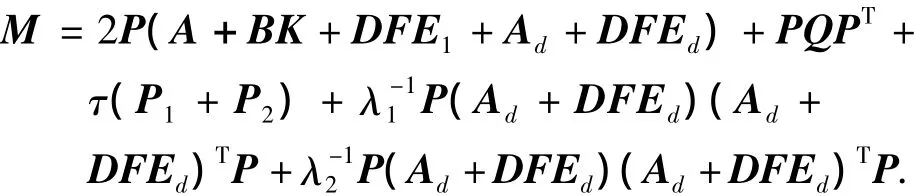
显然，若 M(ε)＜ 0，而

做限定［5］αI≤ PPT、βI≤ PPT，则由合同变换得下式:

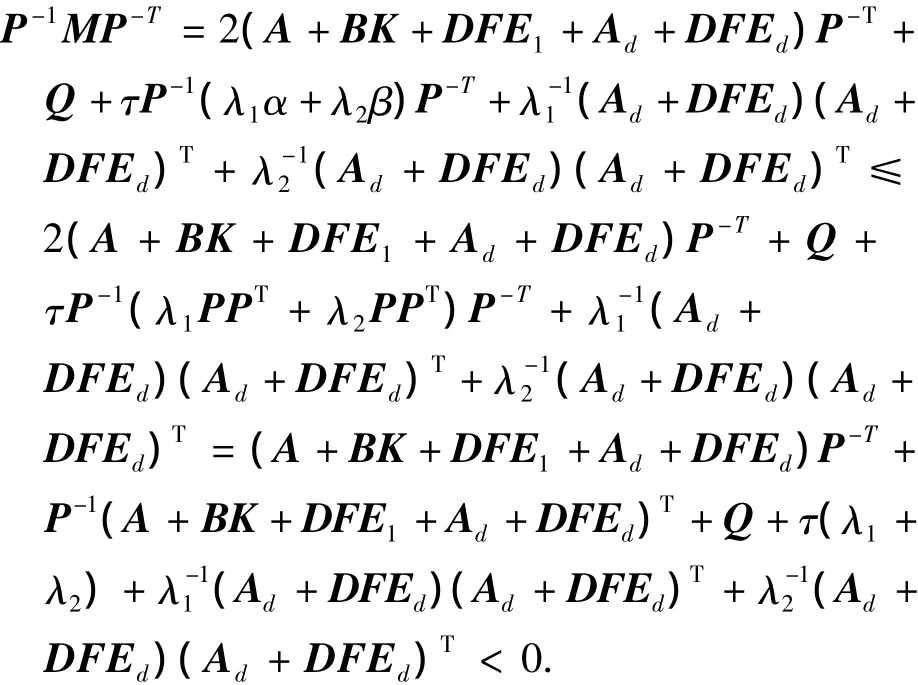
再由Schur补引理，M ＜0等价于下面矩阵不等式成立:

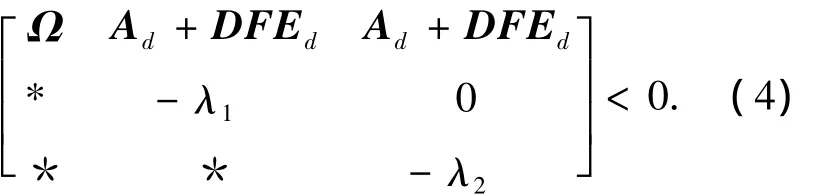
其中“*”号的意义同上，

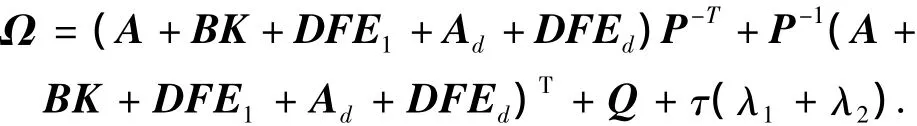
把式(4)作如下处理，以消除不确定:

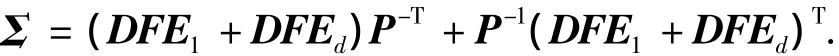
由引理2知，存在 η ＞ 0，使得P－1MP－T＜ 0，等价于

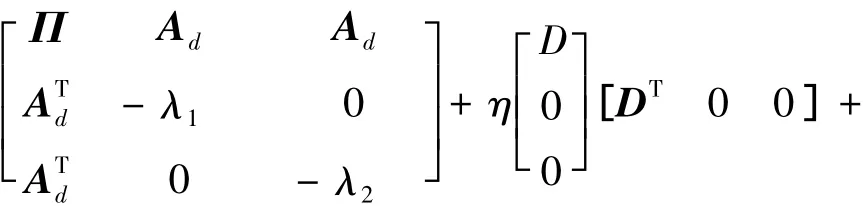
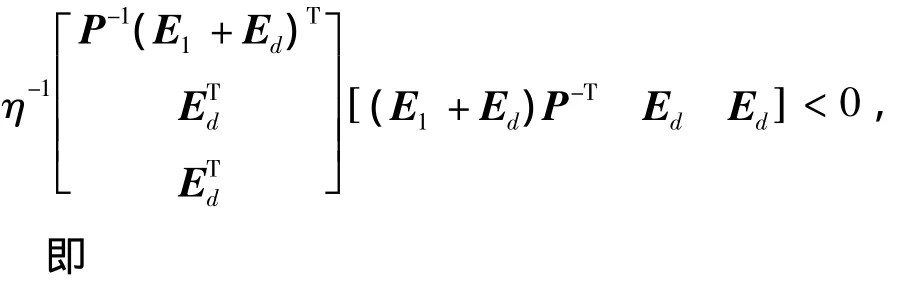
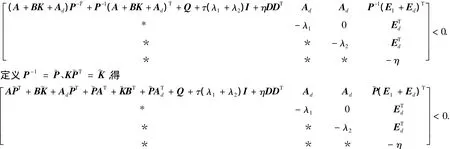
证毕

在系统(1)中，令E1=0，Ed=0，得到如下矩阵不等式:

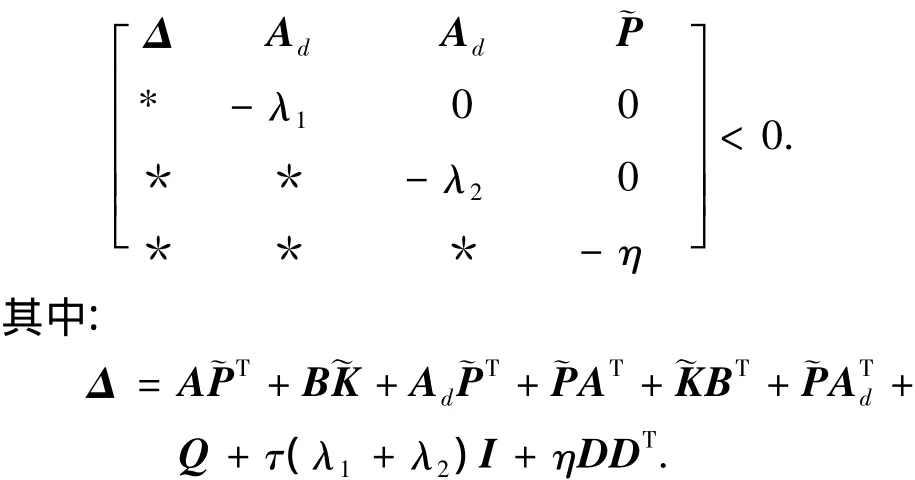
这正是正常系统的稳定性条件［6］.

3 结论

本文考虑一类带时变时滞的不确定系统，研究系统的鲁棒控制器设计问题.所得控制器设计方法描述为线性矩阵不等式形式，容易利用现有优化方法求解相关问题［5，7］.与现有文献［8 －10］相比，系统不确定性结构更加具体.因此，所提方法易于实现且具有广泛的应用前景.

［1］MA X J.Research on robust stability and robust control for uncertain time-de1ay systems［D］.Guangzhou:South China Univisity of Technology，2005:14 －15.

［2］CAO Y Y，SUN Y X.Robust stability of uncertain systems with time-varying multistate delay［J］.IEEE Trans Autom Control，1998，43(3):1484 －1488.

［3］俞立.鲁棒控制——线性矩阵不等式处理方法［M］.北京:清华大学出版社，2002:174－176.

［4］JIANG X F，XU W L.Robust exponential stabilization for linearly uncertain time-delay systems［J］.Journal of Tsinghua University，2004，44(7):997 －1000.

［5］SUTHEE P，FURUTA K.Memoryless stabilization of uncertain linear systems including time-varying state delays［J］.IEEE Trans Autom Control，1989，34(2):460－462.

［6］MEI Ping.Stability analysis for singularl perturbed systems with time-varying delay［J］.Journal of Nanjing University of Science and Technology(Natural Science)，2009，33(3):297－301.

［7］贾新春，郑南宁，张元林.线性不确定时滞系统的可靠保性能鲁棒控制［J］.自动化学报，2003，29(6):971－975.

［8］GLIZER V Y，FRIDMAN E.Stability of singularly perturbed functional-differential systems:spectrum analysis and LMI approaches［J］.IMA Journal of Maths Control＆ Information，2012，29(1):79 －111.

［9］FRIDMAN E.Stability of singularly perturbed differential differences systems:a LMI approach［J］.Dynamics of Continuous，Discrete and Impulsive Systems，2002，9(2):201－212.

［10］CHEN W H，YANG S T，LU X，et al.Exponential stability and exponential stabilization of singularly perturbed stochastic systems with time-varying delay［J］.Robust Nonlinear Control，2010，20(2):2021 －2044.

Controller design for uncertain time-delay systems

SUN Feng-qi
(Institute of Systems Science，Northeastern University，110819 Shenyang，China)

To eliminate time delay and uncertainty that cause some undesired effects in the actual system，using robust control system design techniques，a feedback gain controller is designed which allows the system to meet design requirements within the allowable range of uncertainty，and reduces the sensitivity of the system.A class of stability control problem for uncertain time-varying delay systems with state delay is investigated.By materializing uncertain structural information and constructing a new appropriate Lyapunov-Krasovskii functional based on LMIS，the controller design method is derived.

schur complement lemma;state feedback control;uncertain time-delay systems

TP2

A

0367－6234(2012)11－0129－04

2012－04－24.

国家自然科学基金资助项目(61020106003).

孙凤琪(1968—)，女，教授.

孙凤琪，jlsdsfq@163.com.

(编辑 张 宏)