碟形砂轮磨削面齿轮的数控规律

彭先龙，李建华，方宗德，苏进展，裴杉杉

（1.西北工业大学 机电学院，710072 西安;2.西北机电工程研究所，712099 陕西咸阳）

碟形砂轮磨削面齿轮的数控规律

彭先龙1，李建华1，方宗德1，苏进展1，裴杉杉2

（1.西北工业大学 机电学院，710072 西安;2.西北机电工程研究所，712099 陕西咸阳）

为制造高精度面齿轮，对用碟形砂轮加工面齿轮的数控磨齿方法进行研究.由插齿刀的齿面确定适用于磨削直齿、斜齿面齿轮的碟形砂轮曲面，分析碟形砂轮磨削面齿轮的展成原理，通过坐标变换建立碟形砂轮磨削面齿轮的齿面方程.根据不同加工方法中刀具位置和运动的等价原则确定磨削面齿轮的数控机床运动规律，为方便编程，将该运动规律用二元Taylor展开式表示.计算数控加工齿面与理论齿面的偏差，计算实例的最大偏差为0.071 9 μm，表明用碟形砂轮磨削面齿轮是可行的，数控规律是正确的，能够达到理想的磨齿精度.

面齿轮;碟形砂轮;磨齿;数控

面齿轮在国外已成功应用于直升机的主传动系统，能减轻齿轮箱重量和提高承载能力［1］，并能简化分流－汇流传动结构［2］.用于面齿轮的加工方法有插齿［3－5］、蜗杆刀具滚齿或磨齿等加工技术.由于插齿加工的齿面精度较低，不能用于航空面齿轮传动.蜗杆刀具滚切、磨削面齿轮加工效率高［3，6－7］，但蜗杆齿面受奇异性影响，导致某些参数的插齿刀不存在对应蜗杆，且滚刀或砂轮制造复杂，磨损后的修整困难.

至今，国内外只有格林森公司的H.J.Stadtfeld论述过碟形砂轮磨削面齿轮的方法［8］.采用碟形砂轮磨削面齿轮具有砂轮结构简单，设计制造和修整方便且不受面齿轮设计参数限制的优点.

本文将主要研究碟形砂轮的设计，研究采用碟形砂轮加工面齿轮的磨齿方法及其数控规律.

1 小齿轮和碟形砂轮的齿面

1.1 小齿轮和插齿刀的齿面方程

图1是插齿刀的坐标系，齿面位矢如式(1)所示.

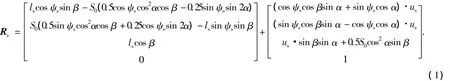
式中:下标s指定插齿刀，下文亦同;ψs为齿轮展成转角，计算方法见文献［4 － 5，7，9］;β 为螺旋角;α是压力角;us、ls是齿面参数;S0=πm/2是分度圆处齿槽宽.插齿刀的单位法矢可由下式表示:

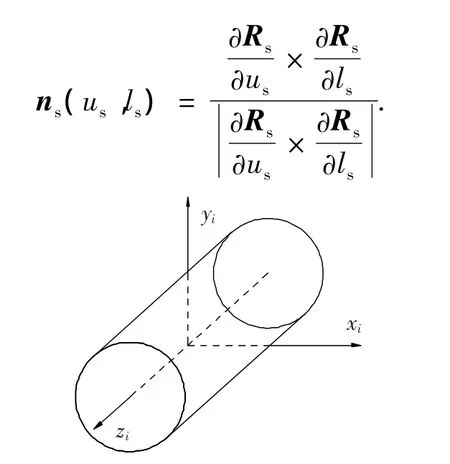
图1 小齿轮和插齿刀的坐标系

1.2 碟形砂轮的设计

碟形砂轮的齿面为一旋转曲面，其产形线是碟形砂轮与插齿刀的接触线［1，9－11］.对于斜齿插齿刀，为了获得接触线的方程必须推导碟形砂轮与斜齿插齿刀的啮合方程，这种方法比较复杂.碟形砂轮的产形线可以通过斜齿插齿刀的端面截线表示，如图2中粗实线所示.将式(1)中的法面压力角α和齿槽宽S0替换为斜齿插齿刀的端面参数，并且令ls和Rs的第三分量为零，即可得到斜齿插齿刀的端面截线.这样处理后，无论是斜齿还是直齿都是适用的.

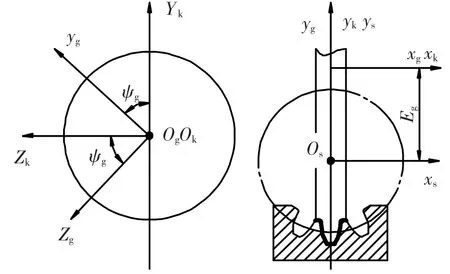
图2 碟形砂轮的确定

图2中的坐标系Ss、Sg和Sk分别与插齿刀、碟形砂轮和机架固联.Eg=rg－rps为碟形砂轮和插齿刀轴线间的距离，其中rg为碟形砂轮的平均半径;rps为插齿刀的分度圆半径.ψg为产形线绕砂轮轴线xg的转角.由坐标变换可导出碟形砂轮的齿面位矢为

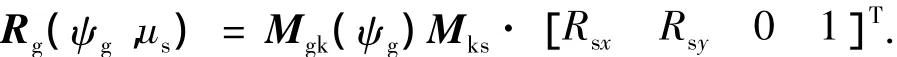
式中，Rsx、Rsy为式(1)中Rs在x轴和y轴上的分量，Mgk、Mks分别表示坐标系Sk到Sg和Ss到Sk的坐标变换矩阵，下文类同.砂轮的法矢为

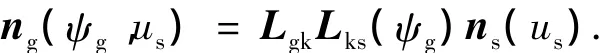
式中Lgk、Lks为由Mgk、Mks删除最后一行和最后一列得到的变换矩阵，下文亦类同.

2 面齿轮

2.1 面齿轮的磨齿原理

碟形砂轮加工面齿轮的磨齿原理如图3所示.图中面齿轮1与插齿刀2啮合，插齿刀2同时与碟形砂轮3啮合，因此碟形砂轮能够与面齿轮正确啮合.在加工过程中，面齿轮绕其回转轴z2旋转，同时砂轮绕插齿刀轴线zs悬摆，砂轮的悬摆模拟了插齿刀的回转运动，这就是面齿轮磨齿的展成运动.砂轮悬摆速度ωs，悬摆角度φs与面齿轮转速ω2和转角φ2满足下式:

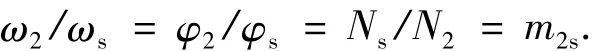
式中Ns、N2、m2s分别是插齿刀的齿数，面齿轮的齿数和插齿刀与面齿轮的传动比.

图3 面齿轮磨齿原理

碟形砂轮、插齿刀和面齿轮三者同时啮合，它们之间的瞬时接触线如图4所示，Lgs是碟形砂轮与插齿刀的接触线，Ls2为插齿刀和面齿轮的接触线.Lgs与Ls2相交于P点，因此碟形砂轮与面齿轮在每个瞬时为点接触.故碟形砂轮绕zs悬摆一个周期，只能在面齿轮上磨出一个带状区域，要磨削出整个面齿轮的齿面，碟形砂轮还必须做平行于zs的直线运动，这就是碟形砂轮的进给运动.当碟形砂轮的位移为Lg时，斜齿插齿刀的转角Δφs为

式中ps是斜齿插齿刀的螺旋参数.则斜齿面齿轮的转角Δφ2为

对于直齿插齿刀和直齿面齿轮Δφs、Δφ2均为零.

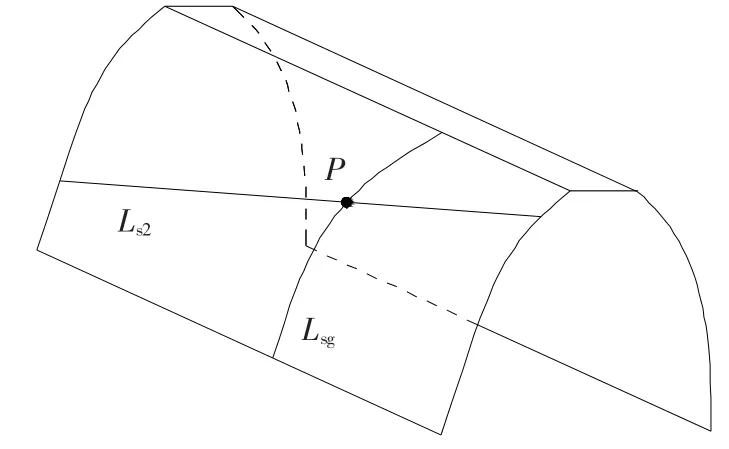
图4 插齿刀齿面上的接触线

用碟形砂轮磨削面齿轮可以看成为双参数包络过程，两组独立的运动参数分别为(φs，φ2)和(Δφ2，Lg).另外，面齿轮磨削的切削运动是砂轮绕轴xg的高速旋转ωg.当切制完一个轮齿后，面齿轮分度，切制下一个轮齿，实行逐齿加工，完成面齿轮所有轮齿的磨削.

2.2 面齿轮的齿面方程

面齿轮展成坐标系如图5所示，Sg、S2和Ss分别与碟形砂轮、面齿轮和原插齿刀固联，其余坐标系为辅助坐标系，L0为面齿轮齿宽中点.

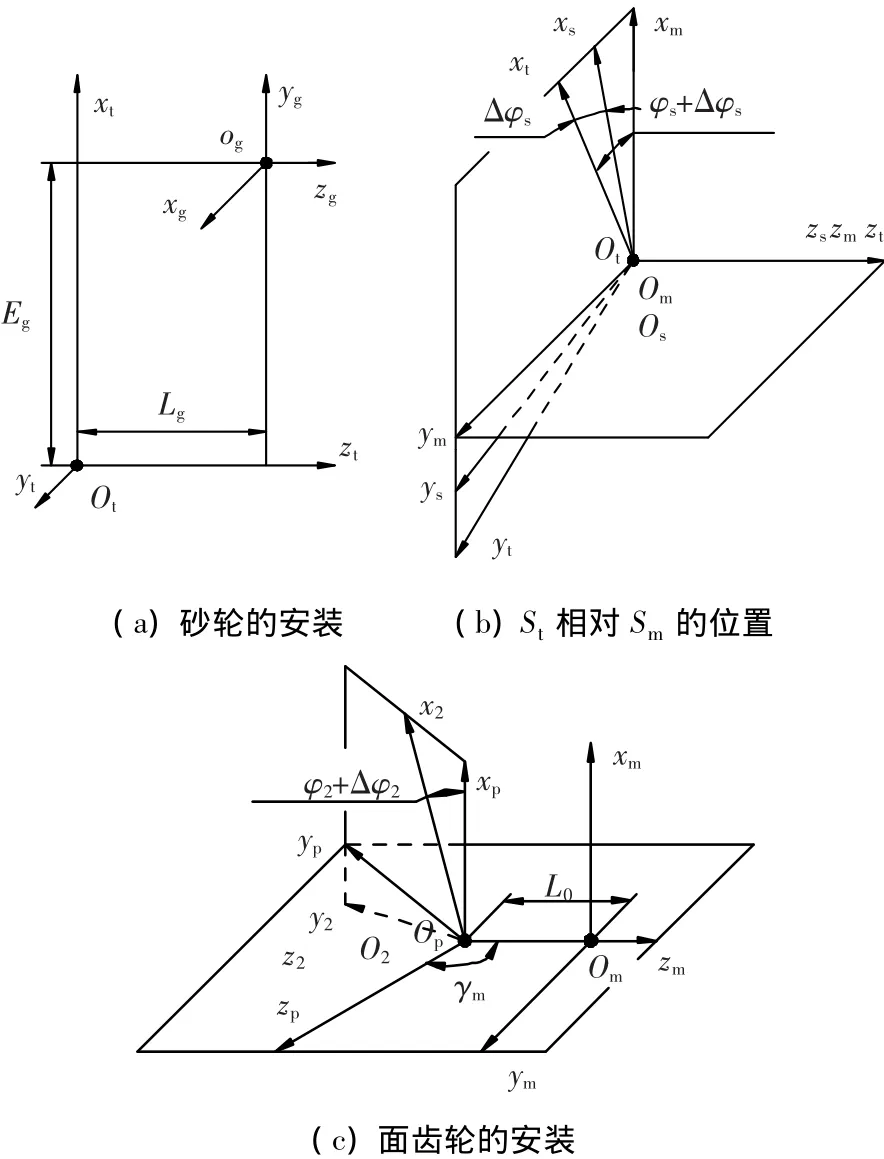
图5 面齿轮展成坐标系

为了简化面齿轮齿面方程的推导，先推导用碟形砂轮表示插齿刀的齿面方程，在坐标系Ss中有

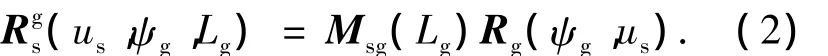
式中，Msg=MstMtg为坐标变换矩阵，上标g表示该插齿刀是由碟形砂轮齿面推导的.碟形砂轮与插齿刀的啮合方程如下:

式中vgsg是碟形砂轮与插齿刀在Sg中的相对速度.

联立式(2)和式(3)即可用碟形砂轮齿面表示插齿刀的齿面方程，并且啮合方程式(3)可以显式表示，即 ψg= ψg(us，Lg)，这种方法比文献［1，9］中的方法简单，但插齿刀齿面法矢需用式(4)确定:

面齿轮的齿面方程由下述方法确定:

式中:M2s=M2pMpmMms为坐标变换矩阵，插齿刀与面齿轮的啮合方程为

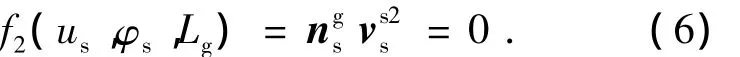
式中vss2为在Ss中插齿刀与面齿轮的相对速度.联立式(5)和式(6)即可表示面齿轮齿面.

3 面齿轮磨齿数控规律

由于用碟形砂轮磨削面齿轮的运动比较复杂，在普通磨齿机床上难以完成.图6是秦川机床厂制造的六轴联动数控机床，由图6可知，平移X、Y和B轴的旋转相当于使砂轮轴绕插齿刀轴线做悬摆运动，与A轴的旋转共同完成展成运动.平移Z相当于进给运动.砂轮轴线的自转是切削运动，不参与齿面的形成过程.

图6 数控机床

由第2节的论述可知，碟形砂轮磨削面齿轮的运动和位置可以表述为

式中(i，j=1，2，3，4)，上标 G 表示面齿轮抽象磨削的坐标变换.

图7是根据图6所示机床定义的数控坐标系，其中xg和z2分别是砂轮和面齿轮的回转轴分，λ、μ是B和A轴的转角.在数控系统中有

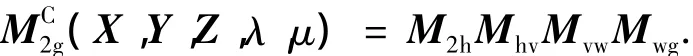
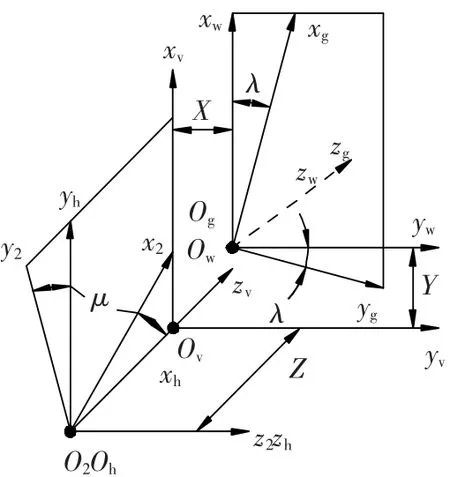
图7 数控机床坐标系

数控方法与抽象方法加工出相同齿面的等价原则是工件与刀具间的相对位置和运动不变［12］，即

最终解得:

为了方便编程，可对式(7)在参考点φs=0、Lg=0处用二元函数的Taylor展开式表示.例如对λ有

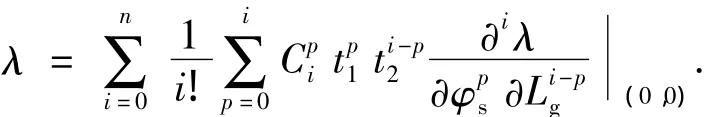
4 算例

以直齿面齿轮和斜齿面齿轮为计算实例，设计参数如表1所示.当n=4时，它们的数控规律分别由式(8)、(9)表示.

定义为数控加工齿面与理论齿面的偏差，斜齿面齿轮的偏差如图8，最大齿面误差为0.071 9 μm.

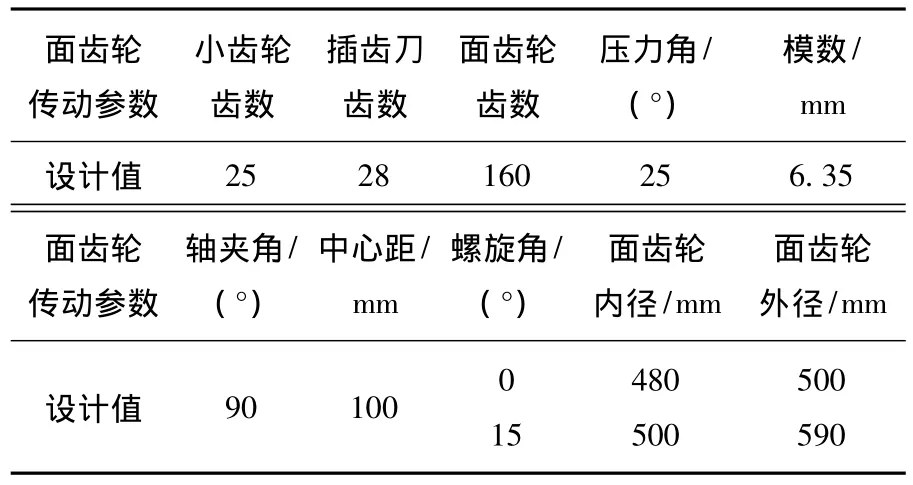
表1 面齿轮设计参数

由式(8)和式(9)可以看出，斜齿面齿轮的数控规律要比直齿面齿轮的数控规律复杂得多，由于B轴不重合于砂轮悬摆轴，导致X、Y向运动复杂.由图8可以看出，用该数控规律加工面齿轮可以达到较高的精度，说明了该加工方法的可行性和数控规律的正确性.

图8 数控加工齿面误差

5 结论

1)设计了直齿、斜齿通用的碟形砂轮.对于斜齿，改进和简化了碟形砂轮的设计，避免了碟形砂轮设计过程中啮合方程的推导.

2)分析了碟形砂轮磨削面齿轮的展成原理，通过坐标变换，建立了碟形砂轮磨削直齿、斜齿面齿轮的齿面方程.

3)根据抽象加工与数控加工中位置和运动的等价原则，建立了面齿轮双参数包络法数控加工模型，因此该模型也适用于蜗杆刀具加工面齿轮的场合.将数控规律用二元Taylor展开式近似表示，以便编程.

4)计算了直齿、斜齿面齿轮的数控规律，数控加工斜齿面齿轮的齿面误差为0.071 9 μm，说明了该数控规律的正确性.

［1］LITVIN F L.Gear geometry and applied theory［M］.Second edition.New York:Cambridge University press，2004:508－546.

［2］BILL R C.Summary highlights of the advanced rotorcraft transmission(ART)program［R］.Washington:American Institute ofAeronautics， 1992:AIAA Paper，92－3362.

［3］LITVIN F L，FUENTES A.Face gear drive with helical involute pinion:geometry，generation by a shaper and a worm，avoidance of singularities and stress analysis［R］.Washington:NASA Center for Aerospace Information，2005:NASA/CR—2005－213443.

［4］沈云波，方宗德，赵宁，等.斜齿面齿轮几何传动误差的设计［J］.航空动力学报，2008，23(11):2147－2152.

［5］赵宁，曾晓春，郭辉，等.斜齿面齿轮齿面仿真及轮齿接触分析［J］.航空动力学报，2008，23(10):1927－1932.

［6］LITVIN F L，FUENTES A，ZANZI C，et al.Face gear drive with spur involute pinion geometry，generation by aworm，stress analysis［J］.computer methods in applied mechanics and engineering，2002，191(25/26):2785－2813.

［7］郭辉.面齿轮滚齿加工方法及其啮合性能研究［D］.西安:西北工业大学机电学院，2009:11－53.

［8］STADTFELD H J.Coniface face gear cutting and grinding［CB/OL］.Kassel:Gleason Corporation，(2010)［2011 －07 －15］.http://www.gearsolutions.com/article/detail/6020/coniface-face-gear-cutting-and-grinding.

［9］LITVIN F L，FUENTES A，GONZALEZ-PEREZ I，et al.Modified involute helical gears:Computerized design，simulation of meshing and stress analysis［J］.computer methods in applied mechanics and engineering，2003，192(33/34):3619－3655.

［10］ZANZI C，PEDRERO J I.Application of modified geometry of face gear drive［J］.computer methods in applied mechanics and engineering，2005，194(27/28/29):3047－3066.

［11］LITVIN F L，FUENTES A，ZANZI C.Design，generation，and stress analysis of two version of geometry of face gear drives［J］.Mechanism and Machine theory，2002，37(10):1179－1211.

［12］LITVIN F L，CHEN N X.Generation of gear tooth surface by application of CNC machines［R］.Washington:NASA center for aerospace information，1995:NASA/CR 1995－195306.

Computer numerical controlling rules for applying grinding disk in face gear grinding

PENG Xian-long1，LI Jian-hua1，FANG Zong-de1，SU Jin-zhan1，PEI Shan-shan

(1.School of Mechanical Engineering，Northwestern Polytechnical University，710072 Xi'an，China;2.Northwest Institute of Mechanical＆ Electrical Engineering，712099 Xianyang，Shanxi，China)

To manufacture face gear with high precise，computer numerical controlled(CNC)grinding method and grinding disk in face gear machining was investigated.The tooth surface equation of face gear machined by grinding disk was determined by coordinate transformation.The motion laws of CNC machine were established by the equivalence principle of position and movement of tool in different machining method，and then the laws were transformed into Taylor expansion for convenient programming.The deviation of CNC machining tooth surface from that of theoretical was calculated，in an illustrated example the maximal deviation was 0.0719 micrometers.The result shows that the grinding method of face gear is feasible，the CNC motion laws are correct and the desired precision is easy to meet.

Face gear;Grinding disk;Grinding;Computer numerical controlling

TH132.41

A

0367－6234(2012)11－0101－04

2011－07－23.

国家自然科学基金资助项目(50875211).

彭先龙(1982—)，男，博士研究生;

方宗德(1942—)，男，教授，博士生导师.

彭先龙，pxljsh@126.com.

book=196,ebook=345

(编辑 杨 波)