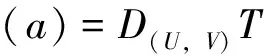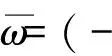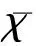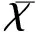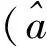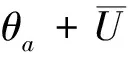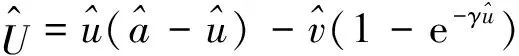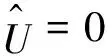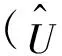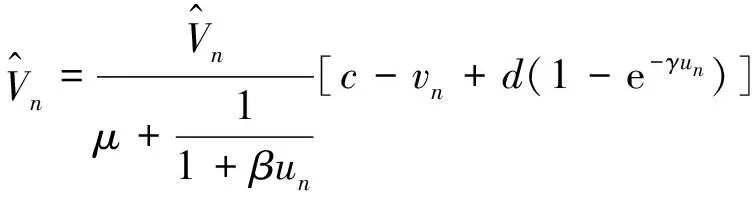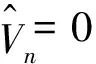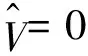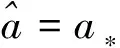具有非线性扩散的捕食-食饵模型的整体分歧*
郭改慧,李兵方
(1.陕西科技大学理学院,陕西 西安 710021;2.陕西铁路工程职业技术学院,陕西 渭南 714000)
基于害虫的生物控制、化学控制和综合管理策略,考虑非线性扩散的捕食-食饵模型
(1)
其中Ω是Rn中具有光滑边界的有界开区域,u和v分别表示食饵(害虫)和捕食者(天敌)的种群密度,γ代表捕食者的捕食效率,d代表食饵转化为捕食者的转化率。 参数a,γ,d均为正常数,c可正可负,c>0表示捕食者有其他的捕食来源。
在模型(1)中,1-e-γu即为Ivlev型功能反应函数,最早由Ivlev[1]提出。对无扩散情形,文[2]得到食饵灭绝和持续生存的充分条件。对一般扩散情形,即(α,β)=(0,0),文[3]利用分歧理论得到分歧正解的存在性和稳定性。对带此类非线性扩散项的Lotka-Volterra捕食-食饵模型,文[4]给出局部分歧解的存在性,并讨论了非线性扩散对捕食过程的影响。
由于种群间的相互影响在种群扩散中起着非常重要的作用,带非线性扩散项的生物模型越来越受到国内外学者的广泛关注[5-6]。鉴于以上研究背景,本文在文[3]的基础上进一步讨论带有非线性扩散项的情况。实践证明,非线性扩散项的引入使问题变得更加复杂。
1 正解的先验估计
令λ1(p,q)<λ2(p,q)≤λ3(p,q)≤…是特征值问题
-pΔφ+q(x)φ=λφ,x∈Ω,φ=0,x∈∂Ω
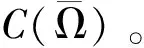
-Δu+q(x)u=au-u2,x∈Ω,u=0,x∈∂Ω
(2)
由文[7]知,如果a≤λ1(q),那么u=0是(2)的唯一非负解,而当a>λ1(q)时,(2)存在唯一正解。当a>λ1时,记唯一正解为θa。而且,θa关于a单调递增,连续可微,并对任意x∈Ω,0<θa
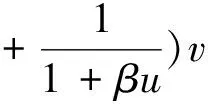
(3)
则(U,V)≥0和(u,v)≥0之间存在一一对应关系。因此关注与(1)等价的椭圆方程
(4)
其中u=u(U,V),v=v(U,V)作为(U,V)的函数由(3)式唯一确定。
当a>λ1,c>(μ+1)λ1时,(4)除平凡解(0,0)外,还存在两个半平凡解(U,V)=(θa,0)和(U,V)=(0,(μ+1)2θc/(μ+1))。由Poincare不等式易得(4)正解存在的必要条件。证明略。
定理1 若a≤λ1或c<μλ1-d,则(4)没有正解。
定理2 设a>λ1,c+d>μλ1。 若(U,V)是(4)的任一正解,则对任意x∈Ω,有
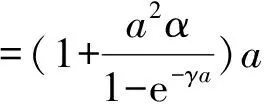
0 (1+1/μ)min{c+d,c+dγM(a)} -ΔU(x1)=u(x1)(a-u(x1))- v(x1)(1-e-γu(x1))≥0 0 -ΔV(x2)=v(x2)(c-v(x2)+d(1-e-γu(x2)))≥0 因此v(x2)≤c+d(1-e-γu(x2)) (1+1/μ)min{c+d,c+dγM(a)} 当c>(μ+1)λ1时,类似文[5]可得V(x)的正下界估计。证明略。 定理3 设a>λ1,c>(μ+1)λ1,则V(x)≥μ(μ+1)θc/(μ+1)。 f(u,v)=u(a-u)-v(1-e-γu), g(u,v)=v(c-v+d(1-e-γu)) 其中u和v均为(U,V)的函数。将(4)在(U,V)=(θa,0)处Taylor展开得 (5) 对(3)式两边关于(U,V)求导得 构造集合S1:={(a,c)∈R2: 引理1 设μλ1-d S1={(a,c)∈R2:a=a*(c), μλ1-d 且满足a*((μ+1)λ1)=λ1,limc→(μλ1-d)+a*(c)=+∞。 证明令 (∂S1(a*(c),c)/∂a)·a*(c)+ ∂S1(a*(c),c)/∂c=0 由引理1知,当μλ1-d 定理4 设μλ1-d Γ*={(a(s);θa*+s(φ*+Φ1(s)), s(ψ*+Ψ1(s))):0 显然ψ≢0。注意到引理1可得ψ=ψ*,从而有 φ=φ*:=(-Δ-a*+2θa*)-1· dimN(L(a*;0,0))=1,codimR(L(a*;0,0))=1 L1(a*;0,0)·(φ*,ψ*)= 假设存在(h,k)∈X使得L1(a*;0,0)·(φ*,ψ*)=L(a*;0,0)·(h,k),则有 上式两边同乘以ψ*,分部积分得 · (6) 由于θa关于a严格单调递增,等式(6)左边大于0,矛盾。 由Crandall-Rabinowitz局部分歧定理[8]知结论成立。 下面以a为参数考察(4)发自半平凡解分支(a;0,(μ+1)2θc/(μ+1))的局部分歧正解。 构造集合 a>λ1} 类似引理1可得 引理2 设c>(μ+1)λ1,则存在单调递增函数a=a*(c)使得 S2={(a,c)∈R2:a=a*(c),c>(μ+1)λ1} 且满足a*((μ+1)λ1)=λ1,limc→+∞a*(c)=+∞。 由引理2知,当c>(μ+1)λ1时,存在唯一a*>λ1使得S2(a*,c)=0。此时不妨设φ*>0 满足 定理5 设c>(μ+1)λ1,则(a*;0,(μ+1)2θc/(μ+1))∈R+×X为(4)的分歧点,且在(a*;0,(μ+1)2θc/(μ+1))的邻域内存在正解 Γ*={(a(s);s(φ*+Φ2(s)),(μ+1)2θc/(μ+1)+ s(ψ*+Ψ2(s))):0 这一节主要借助文[9]中的讨论将定理4、定理5得到的局部分歧延拓为整体分歧。 Δμ1Δχ-qa(x)χ (i)M在R+×X内由(a*;θa*,0)延伸到∞; 下面证明(i)成立。只要说明M-{(a*;θa*,0)}⊂P,(ii)和(iii)即可排除。反证。假设M-{(a*;θa*,0)}P,则存在点;,∈(M-{(a*;θa*,0)})∩∂P和序列{(an;Un,Vn)}⊂M∩P,使得当n→∞时,(an;Un,Vn)→;,易知∈∂P1或∈∂P1。假设∈∂P1,则要么存在x0∈Ω使得,要么存在x0∈∂Ω使得由于满足方程 因此M-{(a*;θa*,0)}⊂P。由定理2知,‖U‖∞,‖V‖∞有界。由LP估计和Sobolev嵌入定理知‖U‖C1、‖V‖C1有界。因此正解分支M在正锥内只能沿参数a延伸到∞。 事实上,以上关于分歧解走向的讨论给出了正解存在的充分条件。 定理6 如果μλ1-d 类似可得 定理7 如果c>(μ+1)λ1且a>a*,那么方程(4)至少存在一个正解。 注1 注意到(u,v)≥(0,0)和(U,V)≥(0,0)之间存在一一对应关系,定理6和定理7给出了方程(1)正解存在的两个充分条件。 参考文献: [1]IVLEV V.Experimental ecology of the feeding fishes[M].Yale University Press,New Haven,1961. [2]WU X J,HUANG W T.Dynamic analysis of a one-prey multi-predator impulsive system with Ivlev-type functional[J].Ecological Modelling,2009,220: 774-783. [3]郭改慧,查淑玲.带Ivlev反应项的捕食模型的全局分歧[J].系统科学与数学,2011,31(12):1633-1640. [4]KADOTO T,KUTO K.Positive steady states for a prey-predator model with some nonlinear diffusion terms[J].J Math Anal Appl,2006,323: 1387-1401. [5]GUO G H,WU J H,MA C.Nonlinear diffusion effect on bifurcation structures for a predator -prey model[J].Differential and Integral Equations,2011,24(1/2): 177-198. [6]PAO C V.Strongly coupled elliptic systems and applications to Lotka-Volterra models with cross-diffusion[J].Nonlinear Analysis,2005,60(7): 1197-1217. [7]叶其孝,李正元.反应扩散方程引论[M].北京: 科学出版社,1994. [8]CRANDALL M G,RABINOWITZ P H.Bifurcation from simple eigenvalues[J].J Functional Analysis,1971,8(2): 321-340. [9]WU J H.Global bifurcation of coexistence state for the competition model in the chemostat[J].Nonlinear Analysis,2000,39(7): 817-835.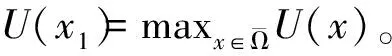
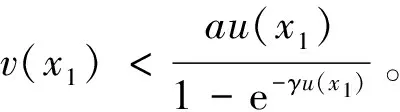
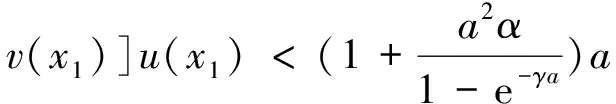
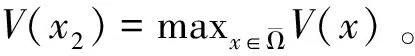
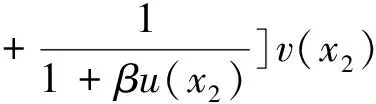
2 局部分歧正解的存在性
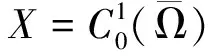
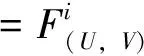

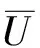
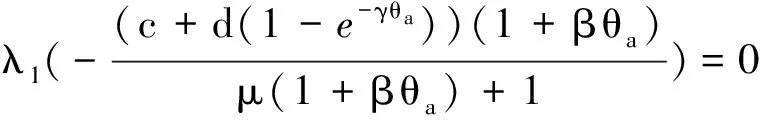

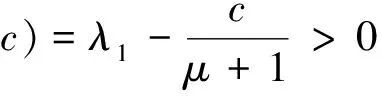
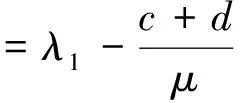
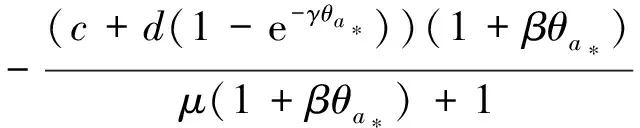
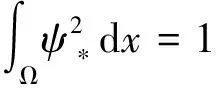
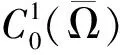
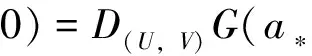
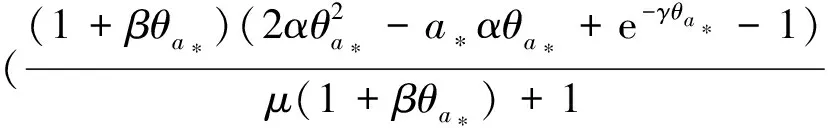
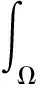
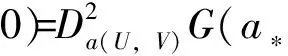
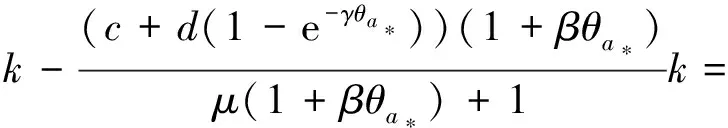
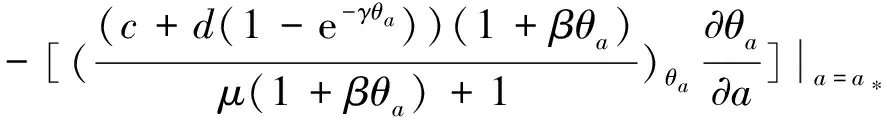

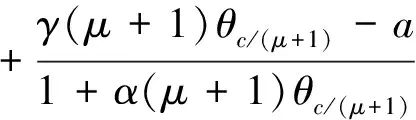
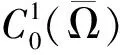

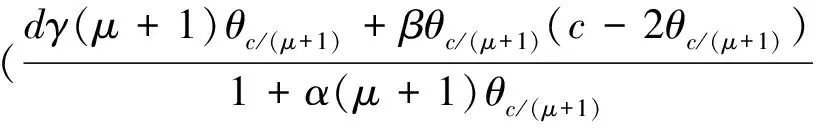
3 局部分歧解的延拓