6类图完美匹配的数目*

唐保祥,任 韩

(1.天水师范学院数学与统计学院,甘肃 天水 741001；2.华东师范大学数学系，上海 200062)

本文所指的图均是有限简单无向标号图(即顶点间是有区别的)，未给出的定义见文献[1]。

图的完美匹配计数是匹配理论的一个重要方面，它既与组合论中棋盘的多米诺覆盖问题有关，又与统计晶体物理中的dimmer问题有关[2-3]。此问题有很强的物理学和化学背景。目前，已有一些文献对图的完美匹配作了相关的研究，给出了一些图完美匹配的计数方法[4-13]。遗憾的是，Valiant在1979年证明了，图(即使是偶图)的完美匹配计数是NP-难的问题。因此，计算出一般图的完美匹配数是困难的，特别是要得到显式的计算公式是更加困难，只有对具有特殊结构或形状的部分图，才可以给出其完美匹配数的显式计算表达式。本文用划分，求和，再递推的方法给出了6类图完美匹配数的显式表达式，所给方法，适合于整体是“条形”的，相同结构重复出现的很多图类完美匹配数目的求解。

1 基本概念

定义1 若图G的两个完美匹配M1和M2中有一条边不同，则称M1和M2是G的两个不同完美匹配。

定义2 设G是2连通平面图，其每个内部面都是边长为1的单位正方形，所有的正方形构成一个m×n的矩形，其中m和n是正整数，则称G为m×n的棋盘。本文将m×n的棋盘记为Qm×n。

设Qm×n表示一个m×n的棋盘，其中V(Qm×n)={uij|1≤i≤m+1,1≤j≤n+1}，E(Qm×n)={uijukl|i=k且l=j+1,或j=l且k=i+1,1≤i,k≤m+1,1≤j,l≤n+1}。易知m×n的棋盘Qm×n有完美匹配的充要条件是m和n中至少有一个是奇数。

2 结果及其证明

定理1 设图Gi(i=1,2,…,2n)是一个6面体，V(Gi)={vi1,ui1,ui2,ui3,vi2}，E(Gi)={ui1ui2,ui2ui3,ui3ui1,vi1ui1,vi1ui2,vi1ui3,vi2ui1,vi2ui2,vi2ui3}，分别连结Gj与Gj+1的两个顶点uj1与uj+1,1，uj2与uj+1,3(j=1,2,…,2n-1)所得的图记为2-2nV6，如图1所示。σ(n)(n≥1)表示2-2nV6的所有不同的完美匹配数，则σ(n)=8n。

图1 2-2nV6图

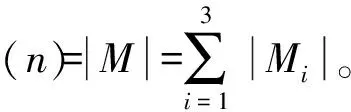
求|M1| 因为v11u11∈M1，所以必有u13v12，u12u23∈M1。此时，若u21v22∈M1，必有v21u22∈M1，M1中这类完美匹配的数目是σ(n-1);若u21v22∉M1，必有v22u22,v21u21∈M1，M1中这类完美匹配的数目也是σ(n-1)。因此，|M1|=2σ(n-1)。类似地可以求得|M2|=2σ(n-1)。

求|M3| 因为v11u13∈M3，所以必有u11v12∈M3，或u12v12∈M3。

情形1u11v12∈M3

因为u11v12∈M3，所以必有u12u23∈M3。此时， 若u21v22∈M3，必有v21u22∈M3，M3中这类完美匹配的数目是σ(n-1);若u21v22∉M3，必有v22u22,v21u21∈M3，M3中这类完美匹配的数目也是σ(n-1)。

情形2u12v12∈M3

因为u12v12∈M3，所以必有u11u21∈M3。此时， 若v21u22∈M3，必有u23v22∈M3，M3中这类完美匹配的数目是σ(n-1);若v21u22∉M3，必有v21u23,v22u22∈M3，M3中这类完美匹配的数目也是σ(n-1)。由情形1和2知，|M3|=4σ(n-1)。

综上所述，图2-2nV6的所有不同完美匹配的数目为σ(n)=8σ(n-1)。易知σ(1)=8，故σ(n)=8n。证毕。

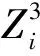
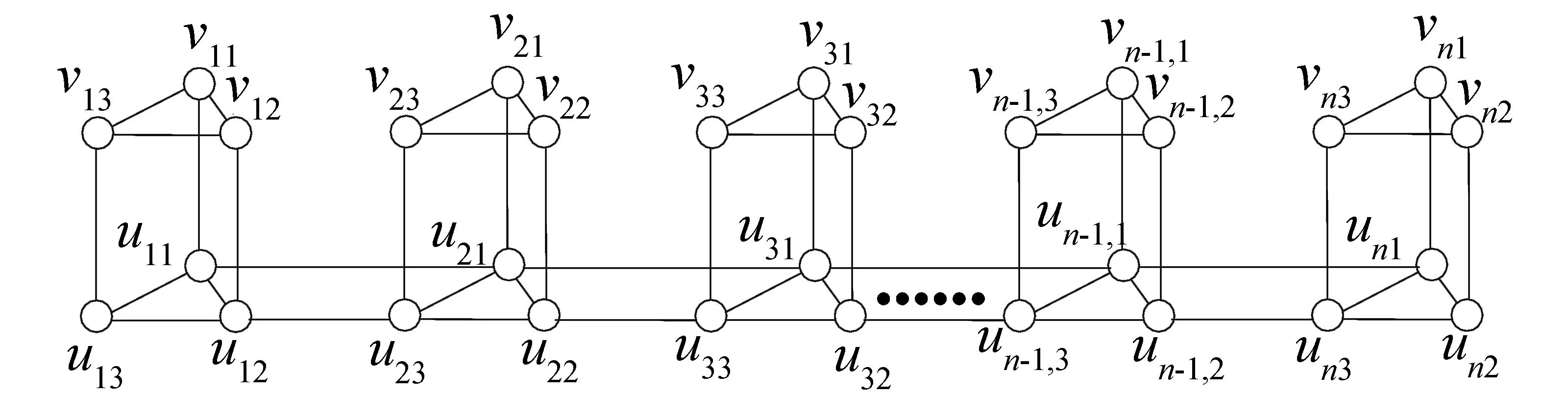
图2 2-nZ3图

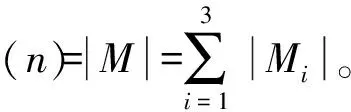
求|M1|

情形1v13u13,v11u11,v12u12∈M1

M1中这类的完美匹配数为τ(n-1)。

情形2v13u13,v11v12,u11u12∈M1

M1中这类的完美匹配数为τ(n-1)。

情形3v13u13,v11v12,u11u21,u12u23,v21v23,v22u22∈M1

M1中这类的完美匹配数为τ(n-2)。因此，|M1|=2τ(n-1)+τ(n-2)。

求|M2| 因为v13v11∈M2，所以必有u13u11，v12u12∈M2。因此，|M2|=τ(n-1)。

求|M3| 因为v13v12∈M3，所以必有u13u12，v11u11∈M3。因此，|M3|=τ(n-1)。

综上所述，

τ(n)=4τ(n-1)+τ(n-2)

(1)

易知τ(1)=4,τ(2)=17。 解线性递推式(1)， 得

证毕。

定理3 设图Bi(i=1,2,…,n)是一个正八面体V(Bi)={vi1,ui1,ui2,ui3,ui4,vi2}，E(Bi)={vi1ui1,vi1ui2,vi1ui3,vi1ui4,ui1ui2,ui2ui3,ui3ui4,ui4ui1,vi2ui1,vi2ui2,vi2ui3,vi2ui4}，分别连结Bj与Bj+1的两个顶点uj1与uj+1,4，uj2与uj+1,3(j=1,2,…,n-1)所得的图记为2-nV8，如图3所示。φ(n)(n≥1)表示图2-nV8的所有不同的完美匹配数，则

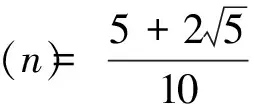
图3 2-nV8图

φ(n)=8φ(n-1)+4φ(n-2)

(2)

易知φ(1)=8,φ(2)=68。解线性递推式(2)，得

证毕。

··2n

图4 2-nZ4图

证明易知图2-nZ4和图G(如图5所示)均有完美匹配。设图G所有不同的完美匹配的数目为g(n)。

图5 G图

容易得到f(1)=9，f(2)=90，f(n)=9f(n-1)+3g(n-2)，g(n)=3f(n)+2g(n-1)。所以

(3)

设图2-nZ4的所有完美匹配的集合为M，则M中不存在仅含边u12u21且不含边u13u24的完美匹配，也不存在仅含边u13u24且不含边u12u21的完美匹配。由于f(1)=9，图2-nZ4不含边u12u21,u13u24的完美匹配数为9f(n-1);图2-nZ4含边u12u21,u13u24的完美匹配数为3g(n-2)。由(3)式，得

·2n-3g(1)

(4)

故

·2n-3g(1)

(5)

从而

3·2n-4g(1)

(6)

由(5)-2·(6)式，得

f(n)=11f(n-1)-18f(n-2)

(7)

定理5 设图Gi(i=1,2,…,2n)是一个6面体，V(Gi)={vi1,ui1,ui2,ui3,vi2}，E(Gi)={ui1ui2,ui2ui3,ui3ui1,)vi1ui1,vi1ui2,vi1ui3,vi2ui1,vi2ui2,vi2ui3}，分别连结Gj与Gj+1的两个顶点vj2与vj+1,1(j=1,2,…,2n-1)所得的图记为1-2nV6，如图6所示。θ(n)(n≥1)表示图1-2nV6的所有不同的完美匹配数，则θ(n)=9n。

图6 1-2nV6图

证明容易得到θ(1)=9，θ(n)=9·θ(n-1)故θ(n)=9n。证毕。

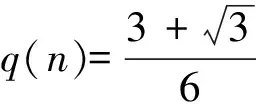
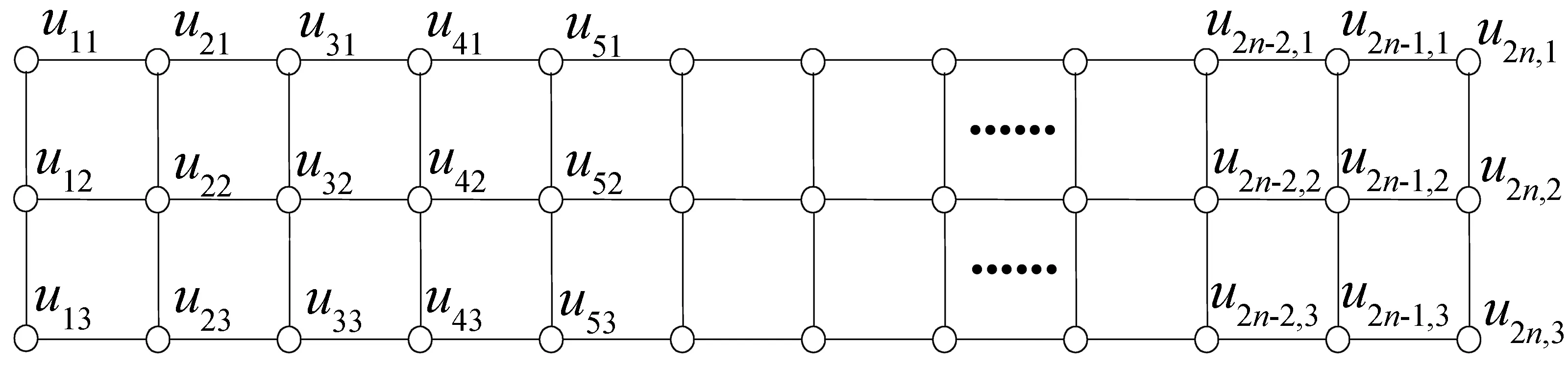
图7 Q2×(2n-1)图

求|M1|

情形(1)u11u12,u21u22,u13u23∈M1，且u21u31,u22u32,u23u33∉M1，如图8所示。由q(n)的定义知，M1中这类完美匹配恰有q(n-1)个。

图8 Q2×(2n-1)图

情形(2)u11u12,u13u23,u21u31,u22u32,u33u43,u41u42∈M1且u41u51,u42u52，u43u53∉M1，如图9所示。M1中这类完美匹配恰有q(n-2)个。

……

情形(n-1)u11u12,u13u23,…,u2n-3,3u2n-2,3,u2n-2,1u2n-2,2∈M1，且u2n-2,1u2n-1,1，u2n-2,2u2n-1,2，u2n-2,3u2n-1,3∉M1，如图10所示。M1中这类完美匹配恰有q(1)个。

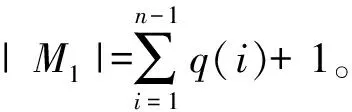
求|M3| 如图11所示，因为u12u22∈M3，所以必有u11u21,u12u22,u13u23∈M3。因此，|M3|=q(n-1)。

图11 Q2×(2n-1)图

所以

q(n)=|M|=2|M1|+|M3|=

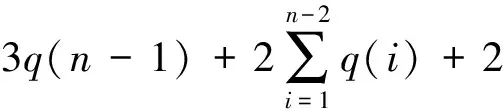
(8)

由(8)式有

(9)

再由(8)-(9)式得

q(n)=4q(n-1)-q(n-2)

(10)

其中n≥3，q(1)=3，q(2)=11。解线性递推式(10)，得

··

证毕。

由定理6，可以直接得到如下推论。

推论1 对任意正整数n，用d(n)表示3×2n棋盘Q3×2n的1×2多米诺覆盖数目。则

··

证明因为3×2n棋盘Q3×2n的每一个1×2多米诺覆盖，都唯一对应2×(2n-1)棋盘Q2×(2n-1)的一个完美匹配；反过来，对2×(2n-1)棋盘Q2×(2n-1)的任一个完美匹配，都唯一对应3×2n棋盘Q3×2n的一个1×2多米诺覆盖。所以3×2n棋盘Q3×2n的1×2多米诺覆盖的集合与2×(2n-1)棋盘Q2×(2n-1)的完美匹配的集合之间是1-1对应的。所以d(n)=q(n)，故

··

证毕。

例1 2×5棋盘Q2×5的一个完美匹配与3×6棋盘Q3×6的一个1×2多米诺覆盖之间的关系如图12所示。

图12 Q2×5和Q3×6图

参考文献：

[1]BONDY J A,MURTY U S R.Graph theory with applications [M].New York : Macmillan Ltd Press,1976.

[2]KASTELEYN P W.The number of dimmer on a quadratic lattice [J].Physica,1961,27:1209-1225.

[3]KASTELEYN P W.Dimmer statistics and phase transition [J].Math Phys,1963,4:287-293.

[4]BRIGHTWELL G R,WINKLER P,HARD C,et al.Adventures at the interface of combinatorics and statistical physics [J].ICM,2002,III: 605-624.

[6]ZHANG H P.The connectivity of Z-transformation graphs of perfect matchings of polyominoes [ J ].Discrete Mathematics,1996,158(1/3): 257-272.

[7]ZHANG H P,ZHANG F J.Perfect matchings of polyomino graphs [J].Graphs and Combinatorics,1997,13: 259-304.

[8]张莲珠.渺位四角系统完美匹配数的计算[J].厦门大学学报：自然科学版,1998,37(5): 629-633.

[9]张莲珠.两类四角系统的匹配数与点独立集数[J].数学研究,1999,32(3): 97-102.

[10]林泓,林晓霞.若干四角系统完美匹配数的计算[J].福州大学学报：自然科学版,2005,33(6): 704-710.

[11]YAN W G,ZHANG F J.Enumeration of perfect matchings of a type of Cartesian products of graphs [J].Discrete Applied Mathematics,2006,154: 145-157.

[12]于青林,刘桂真.图的因子和匹配可扩性[M].北京: 高等教育出版社,2010.

[13]唐保祥,任韩.几类图完美匹配的数目[J].南京师范大学学报：自然科学版,2010,33(3):1-6.