EMD端点效应的改进型混沌延拓方法及其在机械故障诊断中的应用

蔡艳平，李艾华，石林锁，何艳萍，赵静茹

（第二炮兵工程学院五系，西安 710025）

1998 年，Huang［1］提出了基于经验模态分解的EMD算法，EMD算法和与之相应的Hilbert谱统称为Hilbert-Huang变换。Hilbert-Huang变换方法在处理非平稳、非线性信号方面具有独特的优势，但此方法在实际应用中还存在一些问题，其中端点效应引起的问题最为突出［2－12］。目前已有许多学者开展这方面的研究，并提出了不同的边界延拓方法。通过分析现有解决EMD端点效应问题的研究成果，本文将其归纳为5类方法：

（1）极值点预测法，如陈忠等人［3］提出了通过添加极值点抑制端点效应的方法，刘慧婷等人［4］提出了基于多项式拟合的端点效应处理方法等；

（2）信号序列的镜像延拓法，如赵进平等人［5］提出镜像延拓算法，法国学者Rilling等人［6］提出的边界极值点镜像延拓方法等；

（3）信号序列预测法，如邓拥军等人［7］提出用神经网络技术对数据序列进行延拓，杨建文等人［8］提出基于AR模型的时间序列边界延拓方法，程军圣等人［9］提出了基于支持矢量回归机技术的边界延拓方法等；

（4）波形延拓法，如Huang等人［10］提出了在信号两端分别添加一组特征波的边界延拓方法，并将该方法申请了美国的专利。胡爱军等人［11］提出了波形特征匹配延拓法等；

（5）窗函数法，如Qi等人［12］提出用窗函数法对数据序列进行延拓，主要是在信号中间加矩形窗，在端点附近加汉宁窗、海明窗或者余弦窗，把窗函数和原信号相乘后的信号再做EMD分解。

上述这些方法的提出，为EMD的工程应用奠定了基础，但这些方法均各有利弊。如极值点预测法，仅以信号端点附近极值点的特征信息决定延拓极值信息，因此，对非平稳信号有时会不能准确反映其真实趋势，无法达到理想的EMD分解结果；镜像延拓算法在信号具有较强的不对称性时，则无论把镜子放在哪里都不可避免的引入人为影响；支持矢量回归机的边界延拓方法具有较好效果，但其预测精度受内积函数、损失函数、核函数、精度参数和惩罚参数经验选择的影响；波形特征匹配延拓法，该法更适用于周期信号或准周期信号，对于非线性、非平稳信号具有局限性。窗函数法由于加上了一个窗，所以会改变原信号。因此，如何根据机械振动信号的非线性、非平稳特点，有针对性地提出适用性强的边界延拓新方法，更好地将EMD应用于机械振动模式分析中，是值得进一步研究的。针对EMD端点延拓问题，本文提出了一种基于改进型最大Lyapunov指数的边界延拓算法。

1 EMD端点效应问题机理分析

在标准EMD中，EMD包络曲线拟合是采用三次样条插值求取的，即先找出信号的所有极大值和极小值点，然后分别用三次样条插值法来对极大值点、极小值点序列插值，从而获得上、下包络，再由上、下包络线求信号的局部均值，以筛出信号的IMF。为了分析EMD端点效应问题，本文首先分析三次样条插值给EMD包络曲线拟合带来的影响。

设插值对象为平面上n+1个点（xi，yi）（i=0，1，…，n），插值点x0＜x1＜x2＜…＜xn；三次样条插值函数s（xi）满足以下3个条件：

（1）s（xi）=yi，i=0，1，…，n；

（2）s（xi）在每个区间［xi－1，xi］（i=0，1，…，n）上是一个三次多项式：

si（x）=ai（x－xi）3+bi（x－xi）2+ci（x－xi）+di，i=0，1，…，n；

（3）s（xi）在整个区间［x0，xn］上有连续的一阶和二阶导数。

s（xi）还应满足下列三种边界条件之一：

（1） 已知s'（x0）=y'0，s'（xn）=y'n；

（2） 已知s″（x0）=y″0，s″（xn）=y″n；

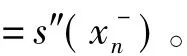
其中第一种和第二中边界条件还可以互相搭配产生新的边界条件，则满足上述条件的s（x）存在且唯一：

其中：hi=xi－xi－1，x∈［xi－1，xi］，i=0，1，…，n

由此可知，对于［x0，xn］以外的外插值点，三次样条插值方法并未给出明确的规定。一般来说，三次样条插值方法对［x0，xn］以外的插值点的插值只是边界点处相邻二点的三次多项式的延伸。

事实上，在EMD分解中，由于信号的两个端点不一定是极值点，无法提供三次样条插值函数所需要条件，所以包络线在端点会产生发散出现，并且这种发散的结果会逐渐向内“污染”整个数据序列而使得结果严重失真，数据越短，其影响越大。

为了便于分析比较现有EMD端点效应解决方法，采用文献［9］、［13］中使用的仿真信号来分析，该信号的表达式为：

仿真信号的采样频率为10 Hz，数据长度为100，EMD的端点效应现象见图1。从图1可见，该包络线在数据两端出现严重失真，尤其是上包络线，发散现象非常严重。

图1 三次样条函数产生的端点效应Fig.1 The end effect of EMD generated by cubic spline function

2 现有EMD端点效应解决方法分析

本文主要分析目前三种典型边界延拓算法：基于镜像延拓的EMD改进算法、基于SVM延拓的EMD改进算法以及基于波形匹配延拓的EMD改进算法。图2给出了镜像延拓及其上下包络线，图3给出了SVM延拓及其上下包络线，图4给出了波形匹配延拓及其上下包络线。

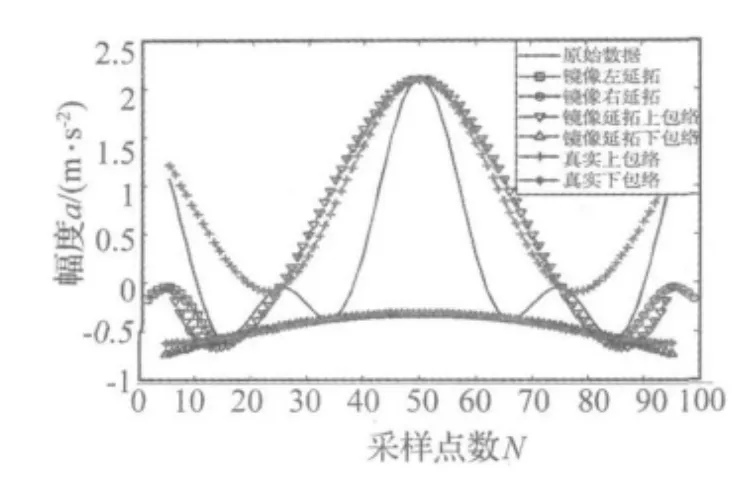
图2 镜像延拓及其上下包络线Fig.2 Mirror extension and its upper and lower envelope of EMD

图3 SVM延拓及其上下包络线Fig.3 SVM extension and its upper and lower envelope of EMD

图4 波形匹配延拓及其上下包络线Fig.4 Waveform matching extension and its upper and lower envelope of EMD

从图2可见，镜像延拓方法对x（t）两端的延拓改善了三次样条包络，但与真实样条包络线相比仍出现了失真，尤其是其上包络线，在信号两端的误差很大，这势必将会影响EMD分解的精度；从图3可见，SVM延拓方法的包络曲线与真实样条包络比较吻合，与镜像延拓方法相比改善效果更好一些，但其上包络线与真实样条包络线相比也出现了部分失真；从图4可见，波形匹配延拓方法对x（t）两端的延拓明显改善了三次样条包络，且与真实样条包络线的变化趋势一致，这说明了波形匹配延拓的有效性。显然，只要原始信号存在一定的规律性，该方法所延拓数据就能延续原始信号的规律。但在实际信号中，如果信号内部没有任何一段波形的变化趋势和边缘处相似，如无规律的强随机性非平稳信号，则该方法的优势将不存在。基于上述分析，本文结合混沌相空间重构理论，提出一种基于改进型Lyapunov指数边界延拓的EMD端点效应处理方法。

3 EMD端点延拓的Lyapunov指数预测模型

由Packard和Takens提出的相空间重构理论，将混沌理论引入到时间序列分析中，系统任意分量的演化是由与之相互作用的其他分量所决定的，因此可以从某一时间序列中提取和恢复出系统原来的规律。对于特定的时间序列：x1，x2，…，xn，如果能找到合适的嵌入维数m和延迟时间τ，则按照Takens定理可以重构其相空间为：

其中：t=（m－1）τ+1，（m－1）τ+2，…，n，N=n－（m－1）τ为相点个数。

3.1 Lyapunov指数预测模型

Lyapunov指数刻画了系统在相空间中的线度指数变化率，因此可将Lyapunov指数作为单序列变量的预报参数。设Lk为某时刻两最近邻点间的距离，经步长Tk后距离演化为L'k+1，并假设在演化过程中L'k+1/Lk近似为一常值，则：

设预测点Y0（t）及其最近邻点Ys（t）经时间T后演化为Y0（t+T）和Ys（t+T），则可得预测方程：

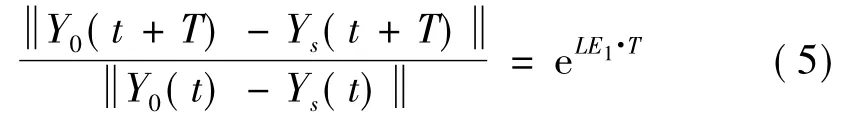
当提前预报时间T≤τ时，Y0（t+T）中只有一个分量x0（t+T）是未知的，解预测方程可得：

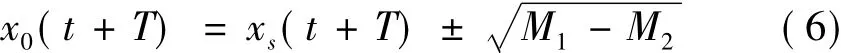
其中：

3.2 Lyapunov指数预测模型的改进

利用最大Lyapunov指数法进行预测时，最大Lyapunov指数表示系统全体轨道在无穷多步演化条件下的平均发散度，因此，Lyapunov指数预测模型仅仅是轨道［Y0（t），Ys（t）］向［Y0（t+1），Ys（t+1）］演化规律的一个近似模型，而真实模型中应该用轨道［Y0（t），Ys（t）］向［Y0（t+1），Ys（t+1）］演化时的发散度代替最大Lyapunov指数，本文对Lyapunov指数预测模型进行改进，步骤如下：

Step1：用互信息法计算时间序列的最佳延迟时间τ，然后再由Cao氏法计算最佳嵌入维数m，重构相空间；

Step2：以局域发散度代替最大Lyapunov指数（基本预测模型同式5）；

局域发散度的计算方法：设参考点为Y0（t），其k个近邻点为Yss（t），ss=1，2，…，k，Yss（t+T）表示近邻点向前演化T（T≤τ）步之后对应的相点。对任意近邻点对（i，j），i，j=1，2，…，k且i＜j，计算：

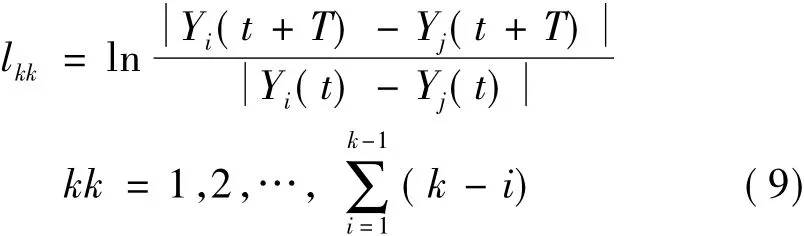
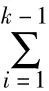
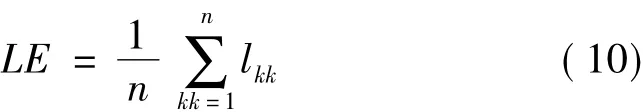
在查询近邻点时不限制短暂分离，考虑夹角，且近邻点个数较少，目的是使近邻点之间的关系能够近似参考点与其最近邻点之间的关系。

4 改进Lyapunov预测模型在端点延拓中的仿真

为了检验本文方法的有效性，分别采用镜像延拓的EMD、波形匹配延拓EMD和基于改进型最大Lyapunov指数延拓EMD对式（2）给出的仿真信号进行EMD分解，图5～图7分别给出各自的EMD分解结果。

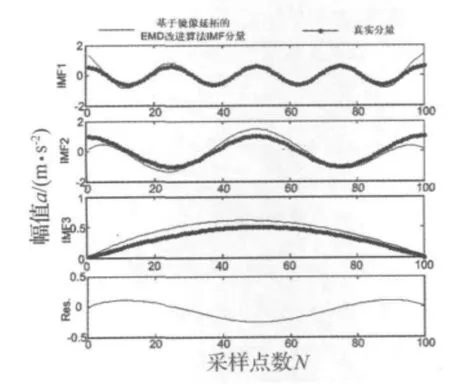
图5 基于镜像延拓的EMD分解Fig.5 The EMD decomposition result based on mirror extension

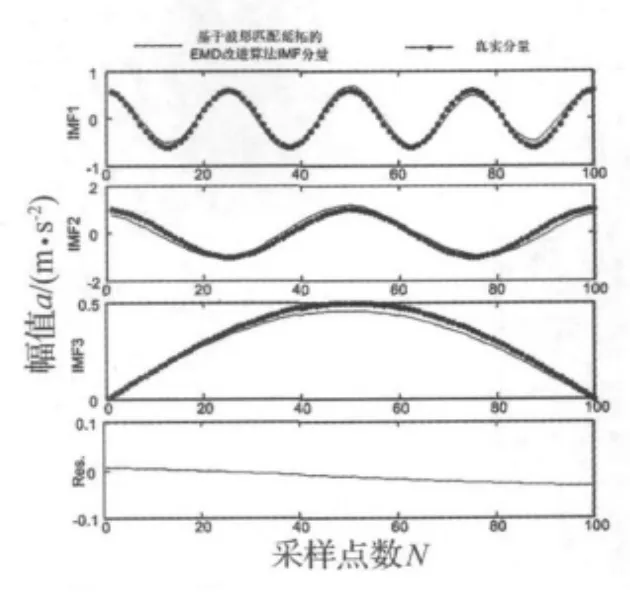
图6 基于波形匹配延拓的EMD分解Fig.6 The EMD decomposition result based on waveform matching extension

图7 基于本文方法的EMD分解Fig.7 The EMD decomposition result based on the proposed method

从图5～图7可以看出：基于改进型最大Lyapunov指数的边界延拓效果最好，具有较好的端点效应抑制能力。相对来说，基于波形匹配延拓方法和镜像延拓法都抑制了端点效应，但二者之间，基于波形匹配延拓方法的结果更胜一筹；基于镜像延拓方法的效果要稍差一点，端点效应仍有较多误差传递至信号内部。

5 旋转机械故障诊断实例

为了检验本文方法在实测信号中应用的有效性，在WS－ZHT1进行模拟油膜涡动故障试验，图8为转子试验台测试系统图。

一般，当转子的转速到达某一转速时，会产生油膜涡动现象，油膜涡动的振动机理如下：轴颈在轴承中转动时会受到油膜的挤压力，当挤压力的切向分量大于阻尼力时转轴将产生涡动，转子绕其轴心线高速旋转，转速为V，当V大于失稳转速时轴颈出现涡动，涡动频率fr约为fV/2，随着转速V上升，涡动频率fr也近似保持这个关系，这种低频振动称为半速涡动，其振幅一般不是很大。油膜涡动的振动特点为油膜涡动的频率接近于转子转速的一半；当转速上升到二倍于轴系的第一阶临界转速时，油膜涡动转变为油膜振荡，表现为转子的振幅增大，转速失稳，且振荡频率不再追踪转速的变化，稳定在某一特定的值（轴系第一阶临界转速）［14－15］。

图8 转子试验台测试系统图Fig.8 Rotor test system

转子油膜涡动的振动时域波形图、频谱图如图9、图10所示。从频谱图10可看出，振动以半频为主，频率约为54 Hz，为转子回转频率108.3Hz 的一半左右，是典型的油膜涡动故障。

为了检验本文方法在提取旋转机械故障特征的有效性，限于篇幅，这里用镜像边界延拓、波形匹配延拓和最大Lyapunov指数边界延拓三种改进EMD方法分别对转子油膜涡动故障振动信号进行分析，见图11～图13。

图11 镜像边界延拓方法分解结果Fig.11 The EMD decomposition result based on mirror extension

在图11中，由上至下依次为原始信号和分解得到的3个IMF分量，第一个内禀模态函数（IMF1）和第二个内禀模态函数（IMF2）的端点产生了一定的发散，使得信号分解结果失真。由于镜像边界延拓方法存在的缺陷，致使EMD分解的结果中出现伪分量IMF3。在图12中，由上至下依次为原始信号和分解得到的2个IMF分量。其中第一个内禀模态函数（IMF1）和第二个内禀模态函数（IMF2）分别对应了信号中1倍频及0.5倍频振动模式，但第一个内禀模态函数（IMF1）和第二个内禀模态函数（IMF2）的端点仍有部分失真。在图13中，IMF1和IMF2分别对应了信号中1倍频及0.5倍频振动模式，且信号两端基本没有出现任何的摆动，分解结果非常理想，其在端点处的变化趋势和原始信号的吻合度高，从高频到低频的2个IMF分量端点效应得到了较好地抑制，包络线的形式和幅值都较为准确，并体现了原始信号的初始相位信息，上述对比说明本文提出的改进型Lyapunov指数边界延拓方法很好地抑制了EMD的端点效应。

为更准确地反映出各EMD改进方法所得的IMF特征信息，对上述各EMD改进方法的IMF分别进行HHT时频分析。图14为用本文改进的EMD方法得到的HHT时频图，图15为用本文改进的EMD方法得到的边际谱图。从图14中可以看出：各谱线两端没有受到端点效应的影响，且时频谱图上主要频率分布为1倍频及0.5倍频成分，同时1倍频有明显的调频现象。从图15中可以看出：0.5倍频成分已高于1倍频，与图10中的幅值谱相比，半频成分能量更为集中，幅值比基频大得多，基频成分准确表示了频率调制范围，在图10中基频成分频率调频特征基本没有显示出来，说明本文改进HHT的时频分析结果能更好地体现油膜涡动的故障特征。

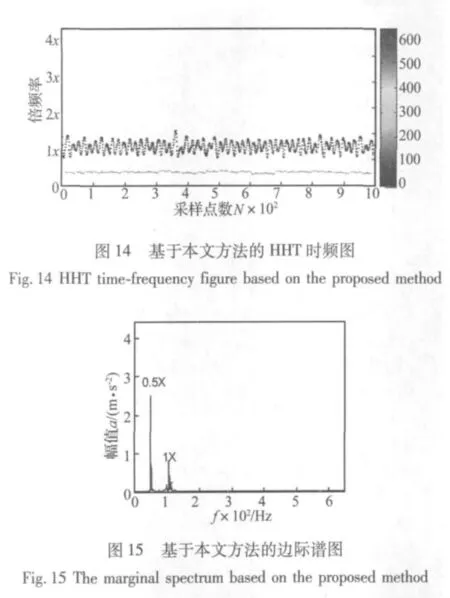
图16为端点不作处理的EMD方法得到的HHT时频图。从图中可以看出，其HHT时频图基本看不出0.5倍频振动模式，且在l倍频信号两端产生了严重的端点效应现象。

图17为用镜像延拓方法得到的HHT时频图。从图中可以看出，基于镜像延拓方法的HHT时频图基本上包含了l倍频和0.5倍频振动模式，但波形存在失真，且在l倍频信号两端产生了一定的端点效应现象。

图18为用波形匹配延拓方法得到的HHT时频图。从图中可以看出，基于波形匹配延拓方法的HHT时频图也基本上包含了l倍频和0.5倍频振动模式，但效果不及改进型最大Lyapunov的边界延拓方法，原因是其0.5倍频振动模式波形存在部分失真。

图18 基于波形匹配延拓方法的HHT时频图Fig.18 HHT time-frequency figure based on waveform matching extension method

对比图14、图16、图17和图18可看出四种方法分解结果的差异所在。显然，本文方法使端点处的延拓更加合理，所延拓数据更加趋于真实。因此，基于本文改进的HHT方法更加准确地提取了转子油膜涡动的故障特征，也进一步说明本文方法的有效性。

6 结论

在HHT应用中，端点效应是必须解决的问题之一，特别是在短数据序列的分析中，端点效应成为影响该方法精度的主要因素。本文在总结现有边界处理方法特点的基础上，结合混沌相空间重构理论，提出一种基于改进型Lyapunov指数边界延拓的EMD端点效应处理方法。其基本原理就是按混沌动力学过程，通过计算时间序列的最大Lyapunov指数，建立混沌预测模型来预测时间序列端点的发展规律，使EMD筛分过程中不会因为端点原因而污染内部数据。在采用最大Lyapunov指数法进行边界延拓时，针对Lyapunov指数预测模型所表示的平均发散度仅是轨道演化规律的一个近似模型，提出采用局域发散度代替最大Lyapunov指数进行改进。通过与现有典型边界延拓方法的仿真对比表明，所提方法的包络线优于其它方法，由于引入了时间序列混沌预测模型使端点处的延拓更合理，所延拓数据更真实；最后将所提方法应用在转子油膜涡动故障诊断中，结果表明该方法能更准确地提取转子油膜涡动故障特征。

需要指出的是，本文所提方法对于无规律具有混沌特征的非平稳信号，在减小HHT的端点效应方面相对其它方法来说具有优势，但由于算法具有一定复杂性，其在计算时间上与神经网络预测算法相当。EMD端点效应是EMD算法中一个非常棘手的问题，这个问题没解决好，EMD算法将毫无用武之地。因此，在实际应用中应视被分析信号的需要来权衡计算精度和计算时间上的利弊进行选择不同的端点效应解决方法。

［1］ Huang N E，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Procedures of the Royal Society of London，Series A，1998，454：903 －995.

［2］沈 路，周晓军，张志刚，等.Hilbert-Huang变换中的一种端点延拓方法［J］.振动与冲击，2009，28（8）：168－171，174.

［3］陈 忠，郑时雄.EMD信号分析方法边缘效应的分析［J］.数据采集与处理，2003，18：1114－1118.

［4］刘慧婷，张 旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004，（16）：84－86.

［5］ Zhao J P，Huang D J.Mirror extending and circular spline function for empirical mode decomposition method［J］.Journal of Zhejiang University（Science），2001，2：247－252.

［6］ Rilling G，Flandrin P，Goncalves P.On Empirical Mode Decomposition and Its Algorithms［A］.In IEEE-Eurasip Workshop on Nonlinear Signal and Image Processing，NSIP－03［C］，Grado（I）.2003.

［7］Deng Y J，Wang W，Qian C C.End-processing-technique in EMD method and Hilbert transform［J］.Chinese Science Bulletin，2001，46（11）：954－961.

［8］杨建文，贾民平.希尔伯特－黄谱的端点效应分析及处理方法研究［J］.振动工程学报，2006，19（2）：283－288.

［9］ Cheng J S，Yu D J，Yang Y.Application of support vector regression machines to the recessing of end effects of Hilbert-Huang transform［J］.MechanicalSystemsand Signal Processing，2007（21）：1197 －1211.

［10］ Huang N E.Empirical mode decomposition apparatus，method and article of manufacture for analyzing biological signals and perfoming curve fitting［P］.United States Patent，2002，6：381.

［11］胡爱军，安连锁，廖贵基.Hilbert-Huang变换端点效应处理新方法［J］.机械工程学报，2008，44（4）：154－158.

［12］ Qi K Y，He Z J.Cosine window-based end processing method for EMD and its application in rubbing fault diagnosis［J］.Mechanical Systems and Signal Processing，2007（21）：2750－2760.

［13］程军圣，于德介，杨 宇.Hilbert-Huang变换端点效应问题的探讨［J］.振动与冲击，2005，24（6）：40－42.

［14］马 辉，李朝峰，轩广进，等.转子系统油膜失稳故障的时频特征分析［J］.振动与冲击，2010，29（2）：193－195，198.

［15］曹冲锋，杨世锡，杨将新.一种基于瞬时能量分布特征的汽轮发电机组转子故障诊断新方法［J］.振动与冲击，2009，28（3）：35－39.