水平井钻柱涡动特性数值分析与试验

王宝金　任福深　朱安贺　赵　蕾

1.东北石油大学机械科学与工程学院，大庆，1633182.中交天和机械设备制造有限公司，常熟，215505　　3.国核工程有限公司，上海，200233

0　引言

水平井可在薄油层中穿越，是稀井增产的重要技术手段，在低压、低渗、薄油藏、稠油藏及常规技术难以取得经济效益的油田开发方面发挥了重要作用。钻柱在旋转钻井过程中，受井眼的限制，底部钻柱的动力学特性和运动状态变得十分复杂。浸泡在钻井液内的旋转受压钻柱在屈曲和涡动的作用下，容易发生磨损、疲劳断裂以及井眼的倾斜。垂直井钻井过程中，钻柱存在涡动现象的事实已被接受。这种钻柱的涡动对钻井作业十分不利，尤其是底部钻柱的反向涡动，会加快钻柱的磨损，易导致钻柱提前疲劳破坏。国内外学者对底部钻柱动力学特性进行了研究。JANSEN等[1-2]和 NAGANAWA等[3]根据非线性转子动力学理论，建立了量纲一钻柱涡动方程，并进行了数值模拟计算。CHRISTOFOROU等[4]借助Rayleigh梁模型对底部钻具组合涡动特性进行了分析，研究结果很好地反映了底部钻柱的涡动特性。DYKSTRA等[5]深入分析了钻头在钻柱涡动时的动力学特征，研究结果表明，钻柱的反向涡动会降低井底与地面设备的能量传递效率。 KHULIEF等[6]研究了钻柱横向振动和涡动的耦合振动、扭转振动和横向振动的耦合振动，并进行了有限元仿真研究。HAYAT等[7]通过模拟试验和仿真分析相结合的研究方法，分析并讨论了底部钻具组合的动力学特性。肖文生等[8]分析了内外钻井液和摩阻作用下钻柱的涡动机理，并得到了钻柱涡动失稳的判定条件。姚永汉等[9]利用编制好的模拟程序分析了钻铤形心的涡动轨迹、涡动速度、径向轨迹、径向速度。狄勤丰等[10]建立了底部钻具组合的动力学仿真模型，把钻具组合简化为转子模型，研究了不同钻压下钻柱的涡动特性。马汝涛等[11]提出利用内摆线法来描述底部钻柱的涡动轨迹。张晋凯等[12-13]和史玉才[14]分析了涡动钻柱内流体的流动特性，根据转子动力学理论建立了考虑钻柱与井壁碰摩作用的涡动方程，探讨了钻柱的涡动产生的机理。2013年，李子丰[15]对钻柱涡动的研究现状做了更进一步的探究，在此基础上提出了流体润滑动力学理论，该理论是研究钻柱涡动必不可少的理论支撑。

目前钻柱涡动的研究大都是针对垂直井或斜直井开展的，对水平井钻柱涡动问题的研究还鲜有报道，甚至水平井钻井过程中是否会存在涡动现象还存在着一定的争议。本文针对水平井钻柱的动力学特征，建立了水平井钻柱的运动方程，并基于自主研制的水平井钻柱动力学试验装置，采用数值模拟和试验研究相互结合的方法，开展了水平井钻柱涡动动力学行为机理的研究。

1　数学模型

钻柱的振动可以分为三个模式：轴向、侧向(也包含横向与弯曲)、扭转模式，它们具有不同的破坏性。钻头的反弹、黏滑、涡动是耦合振动的极端例子，这种耦合通常包括轴向、扭转和侧向运动。这些振动模式通常是由钻头-地层作用、钻柱-井壁的多点接触、质量的不平衡以及振动钻井工具等因素引起的[16]。

旋转钻进过程中，钻柱按转盘转动速度绕自身轴线旋转的同时，由于钻柱与井壁的接触产生摩擦力以及钻井液的作用, 使钻柱以一定的速度按逆时针方向绕井眼轴线旋转, 形成涡动。当钻柱自转方向和绕井眼旋转运动的方向相同时，这种涡动称为正向涡动；当钻柱自转方向和绕井眼旋转运动的方向相反时，称为反向涡动。

钻柱反向涡动形成的必备条件之一是钻柱与井壁碰撞接触，钻柱与井壁产生的周向接触摩擦力是钻柱形成反向涡动的动力源，同时由于钻柱的质量偏心，旋转过程中钻柱会受到离心力作用，钻柱离心力作用会进一步加大钻柱的横向弯曲，增加了钻柱与井壁的碰撞几率，从而促进了后涡的形成，随着涡动角速度的增大，离心力也随着增大，可见，离心力与涡动是相互促进的关系。水平井钻柱在工作时的状态如图1所示。

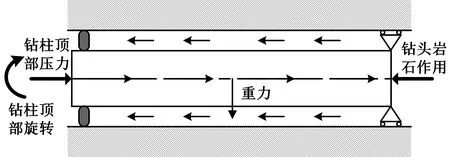
图1　水平井钻柱模型Fig.1　Drillstring in horizontal well

1.1　重力作用下水平井涡动微分方程

钻柱在任意时刻t的运动状态如图2所示。当钻柱浸泡在钻井液的环境下运动时，由于动挠度的影响，钻柱受到的变形恢复力在x、y轴方向的投影可以表示为

(1)

式中，xG、yG为钻柱几何中心的位置；e为偏心距；φ为几何中心-原点连线与x轴的夹角；k为钻柱刚度。

根据质心运动定理，可得钻柱的质心运动微分方程：

(2)

式中，m为钻柱质量。

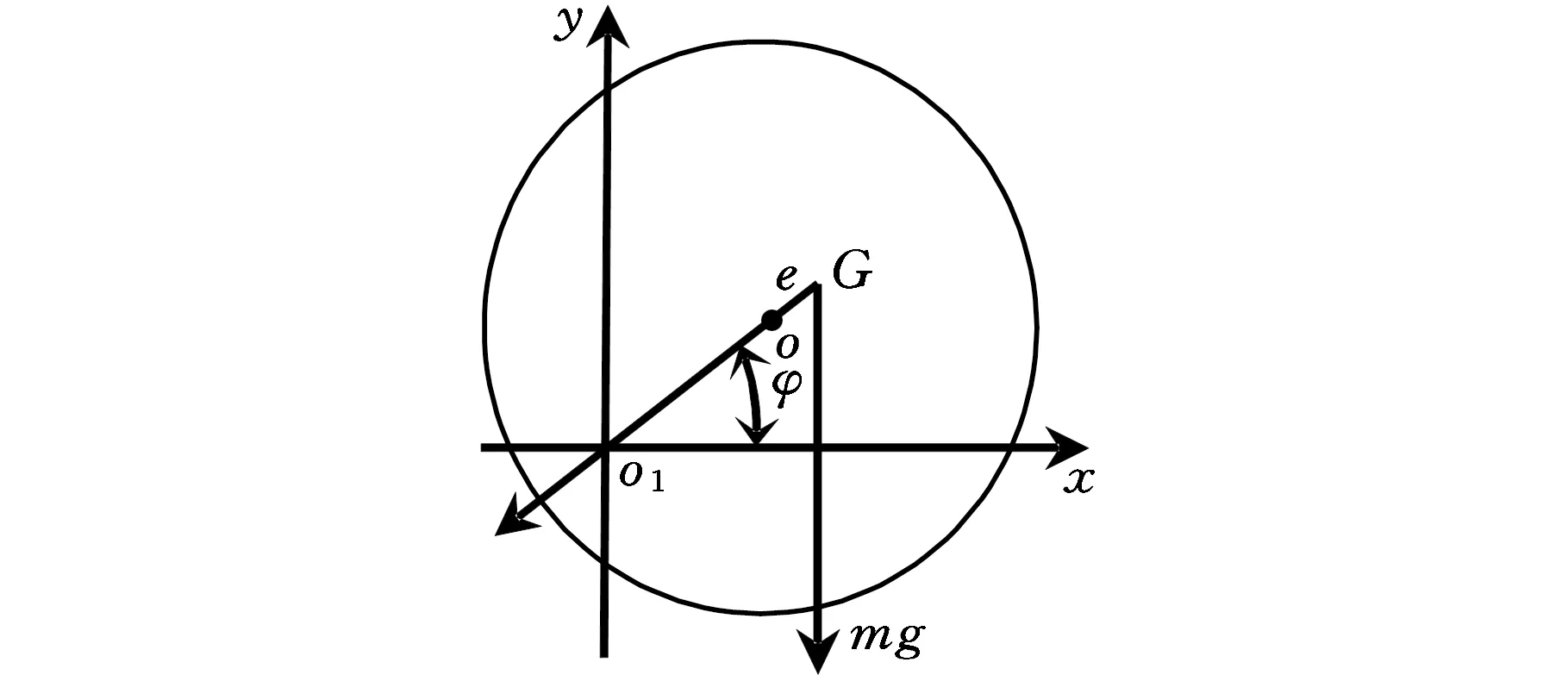
图2　水平钻柱瞬时位置受力分析Fig.2　Force analysis of instantaneous position of horizontal drillstring

根据刚体动量矩定理建立钻柱的转动微分方程，钻柱的动量矩包含以下两部分：

(3)

式中，s为钻柱的回转半径。

(2)钻柱质心对z轴的动量矩为

(4)

即

(5)

为了使方程更加简练，进行坐标变化，把原点从o1点移到G点，并令

xGA=xG+mg/k

(6)

在新坐标系下钻柱的运动微分方程为

(7)

(8)

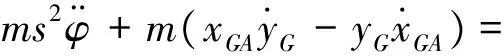
(9)

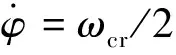
φ=ωcrt/2

(10)

式中，ωcr为临界角速度。

将式(10)代入式(9)得

(11)

联立式(7)、式(9)、式(11)可得

(12)

(13)

式中，δ为钻柱在自重作用下产生的静挠度，δ=mg/k。

根据图2所示的几何关系，可得到钻柱中心的运动方程:

(14)

(15)

由以上分析可知，钻柱几何中心o在副临界时的进动由两个分量组成：与偏心距有关的基频分量、与钻柱本身质量引起的静挠度δ有关的倍频分量，在钻柱旋转过程中，与临界转速相比，重力引起的副临界现象是一个很严重的问题，质量偏心引起的动挠度要比初始时刻的静挠度大得多，因此，在分析水平井钻柱的涡动问题时，钻柱自身质量是一项关键影响参数。

1.2　钻压和井壁摩阻作用下的碰撞机理

钻压作用下的水平井旋转钻柱会发生横向振动，当振动位移大过井眼间隙时就会与井壁发生碰撞，使钻柱的受力发生明显改变，本节主要探讨钻压和摩阻对钻柱涡动的影响。

如图3所示，钻柱以角速度Ω自转，任意时刻在i点接触，受到井壁的法向支持力N以及切向干摩擦力Ft，设钻柱处于完全平衡状态，忽略陀螺效应，这时描述钻柱运动的唯一广义坐标就是回转角φ，其运动的微分方程为

(16)

式中，μ为钻柱与井壁的摩擦因数；c为外阻尼系数；s为钻柱的回转半径；dext为钻柱外径；ω为涡动角速度；vi为i点的钻柱速度。

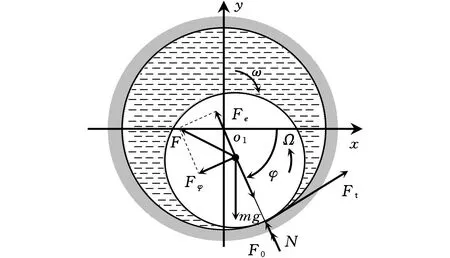
图3　环空内钻井液包围钻柱的受力图Fig.3　Drillstring in annular with drilling fluid

Fw为钻压在径向方向的分力，其表达式为

(17)

式中，pw为钻头所受钻压。

1.3　钻井液作用下的钻柱涡动综合方程

由上述建模和分析可知，钻井液、钻柱自重、井壁摩阻都在一定程度上影响着钻柱的涡动行为，但是还没有考虑内外钻井液流速对钻柱涡动的影响。随钻柱旋转的钻井液会对钻柱内壁施加一定的作用力，加之水平井存在初始弯曲，钻柱的运动和受力会更加复杂多变。

已知钻柱的变形曲线ε(z)，则钻柱内钻井液的流动状态就可以确定，参照图3，钻柱内钻井液流体沿x、y两个方向的作用力线密度分别为

(18)

式中，l为钻柱长度；J为钻柱转动惯量；e为钻井液密度；γ1为常数；Cm为附加质量系数；dint为钻柱的内径;A为钻柱横截面积；dint为钻柱内径。

由式(18)可知，钻柱内钻井液对钻柱的作用力与钻柱的横向变形位移共线，表达式为

(19)

式中，dint为钻柱内径。

钻柱中心坐标为(e,φ)，钻井液对钻柱的总压力F总是指向钻柱的几何中心，F可分解为径向力Fe和轴向力Fφ，Fe相当于钻井液对钻柱施加一个支持力，与钻柱内钻井液对钻柱的作用力方向相反；Fφ沿着钻柱自转方向，使钻柱周向的运动速度增大，可能导致钻柱运动失稳。图3中，钻柱按顺时针方向旋转，取钻柱旋转方向α角为周向坐标，考虑到e、φ变化引起环空内钻井液厚度的变化，可利用Reynolds方程来近似描述这种变化关系[17]：

(20)

h=C(1+εcosα)h

对式(20)积分得环空钻井液的压力分布p=p(α,z)，则有

(21)

式中，R为钻柱半径。

考虑钻井液流速作用下的钻柱涡动的模型如图1所示。当考虑钻井液流速的影响时，流动的钻井液还会对钻柱产生附加质量力和黏滞阻力，钻柱内钻井液对钻柱产生的附加质量力

(22)

式中，ma为钻柱内钻井液质量；v1为钻柱内钻井液流速。

环空内钻井液对钻柱产生的附加质量力

(23)

其中，mb为环空内钻井液质量；v2为环空内钻井液流速；附加质量系数cm的值为

(24)

式中，D为钻柱外直径；Dext为井筒直径。

钻井液阻力[18]

(25)

将式(19)、式(21)～式(25)代入式(16)，得到钻柱在径向方向的整体运动方程：

(26)

FN1=FO-FI+F0f+N-mgsinφ-FW-Fint(z)

求解式(26)，最终可得钻柱轴心轨迹方程：

S=s2φ/2

(27)

其中，钻柱的回转半径s和夹角φ已求得，代入式(27)即可得到钻柱的轴心轨迹在时域内的图像。

2　数值分析与试验

钻柱作业过程中井底环境极其复杂，建立数学模型的过程中难免会简化或忽略一些次要条件，给数值分析带来了一定的不确定性。为了更加真实地反映钻柱的动力学状态，有必要研制相应的试验装置，以得到更为精确和复杂的激励源(例如岩石钻头接触以及钻柱与井筒的摩擦)，进而得到更为接近真相的研究成果。

根据相似准则研制水平受压钻柱试验装置，如图4和图5所示，整个装置主要由以下4个部分组成：钻压施加和转速调节系统、钻井液循环系统、井底模拟系统、数据采集系统。利用该试验装置可以进行不同钻压、转速条件下水平井钻柱动力学特性试验，以及考虑钻井液流速条件下的流固耦合模拟试验。试验过程中可以通过透明有机玻璃井筒实时观测钻柱在模拟井筒中的运动状态。通过相似准则中的单值性条件，将物理现象群中的通解转变为特解，模型与原型物理量间的相似变换式(包含物理条件相似、边界条件相似、起始条件相似)。

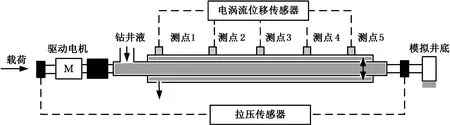
图4　水平井钻柱动力学模拟试验装置示意图Fig.4　Schematic diagram of horizontal drillstring dynamic simulation test apparatus

图5　试验装置Fig.5　Test apparatus

相似转速比为cω，轴向力比为cp，根据相似准则取cp=1/9130，cω=2.8，即试验转速为井场转速的2.8倍，模型钻压是井场实际钻压的1/9130。

表1　试验参数Tab.1　Experimental parameters

试验模型钻柱总长度为10 m，模拟实际100 m钻柱的动力学行为。根据实际钻井经验，钻柱不同位置的动力学特性是不同的，因此，在试验装置中设置了5个测试区，每个测试点间隔2.5 m，如图4所示。

为了具体分析钻柱的动力学特性，分别对钻柱5个测试区的钻柱运动轴心轨迹进行了试验，本文采用两个垂直电涡流位移传感器分别测量钻柱两个垂直方向的位移，最后合成钻柱的轴心轨迹。初步分析结果显示，近钻头第5测试区的钻柱动力学特征较为明显，第3和4测试区相对第5测试区，钻柱的动力学特征变化不明显，到了第2测试区后，钻柱动力学状态相对第5测试区发生了明显的变化，呈现不同的钻柱运动学特征。以下将第5测试区定义为近钻头段，将第2测试区定义为远钻头段，进行钻柱的动力学状态分析。

2.1　远钻头段涡动特性分析

2.1.1转速和钻压对远钻头段轴心轨迹的影响

试验钻压分别为5 N、15 N和25 N，分别调整试验转速为50 r/min、150 r/min和350 r/min，试验和数值仿真结果如图6所示。

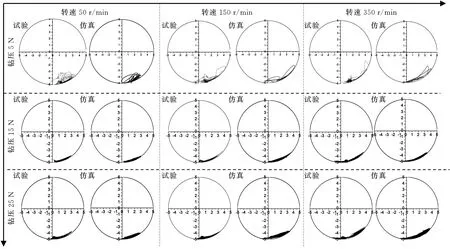
图6　不同钻压、转速下远钻头段钻柱轴心轨迹线Fig.6　Trajectory of drillstring away from bit with different pressure and rotational speed

仿真与试验结果显示，在低钻压(5 N)、低钻速时，远钻头段轴心运动轨迹局限于井眼的右下方，它在井筒上攀升的距离很短，轨迹呈现一种小范围椭圆形状；随着转速的升高，轴心轨迹沿井筒爬升，并且其轨迹变窄；当转速达到350 r/min时，远钻头段运动轨迹线近似为一条细长的圆弧线。

在中高钻压(15～25 N)下，远钻头段轴心轨迹线仍呈“圆弧形”，随着转速的增加，它在井筒上攀升的距离加大。

2.1.2钻井液流速对远钻头段钻柱轴心轨迹的影响

固定试验钻压5 N、转速50 r/min，在0.65～1.25 m/s区间内调整钻井液流速，远钻头段轴心轨迹如图7所示。

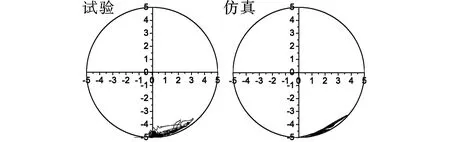
(a)流速为0.65 m/s

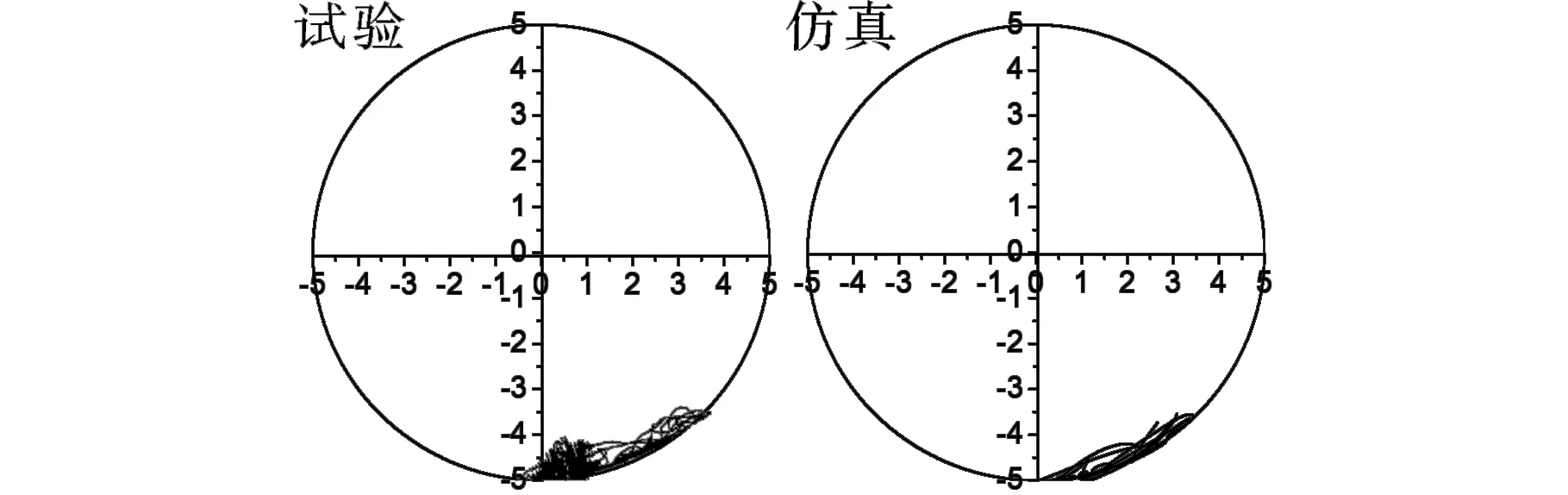
(b)流速为0.95 m/s

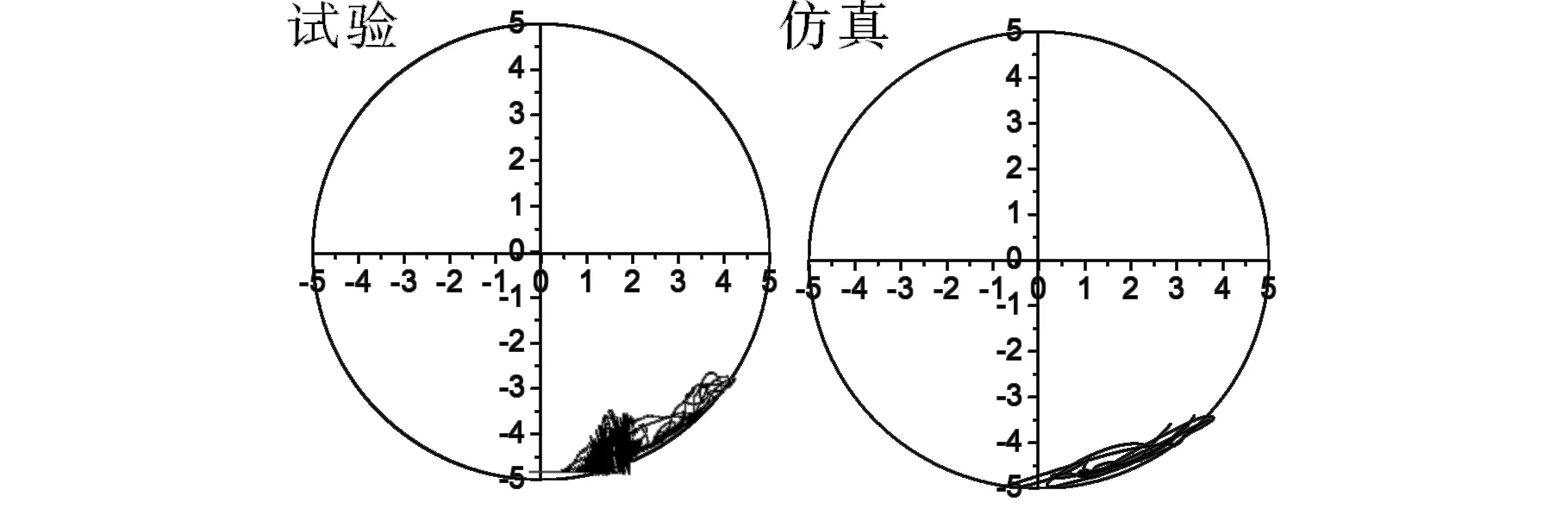
(c)流速为1.25 m/s图7　不同流速下远钻头段轴心轨迹线Fig.7　Trajectory of drillstring away from bit with different flow rate

钻井液的存在没有改变远钻头段的动力学特征，其轴心轨迹线由近似的椭圆形状变成了密集的圆弧曲线，这说明钻井液的存在使得远钻头段在井底的动力学状态趋于稳定。随着钻井液流速的增大，远钻头段的径向运动幅值也在逐渐增大，但是轴心轨迹并没有发生本质变化，依然是周期性的爬坡运动。

由上述分析可以看出，远钻头段轴心轨迹均在第三象限并呈“圆弧形”，转速、钻压以及流体条件的变化，并没有对钻柱的动力学特征产生本质性的改变，且没有出现涡动现象。

2.2　近钻头段涡动分析

由于钻头受到切割岩石的反作用力，工作时易形成行星运动，进而带动与之直接相连的钻柱产生牵连运动。此外，由于钻头与岩石接触所诱发的激励以及其横向与扭转振动的同时存在，使得此段钻柱动力学状态相对复杂。

2.2.1钻压和转速对近钻头段轴心轨迹的影响

固定钻井液流速为1.25 m/s，试验钻压为5 N、15 N和25 N，并且分别调整试验转速为50 r/min、150 r/min和350 r/min，试验和数值仿真结果如图8所示。可发现，试验涡动曲线的第三象限出现了较为平直的曲线，这是由电涡流位移传感器的放置位置以及试验限位装置导致的，造成钻柱在运动至第三象限时，产生了信号干扰，但并未导致采集的信号发生实质变化，由此可以忽略其影响。当转速为50 r/min时，近钻头段一直处于井筒右下方，运动范围始终没有超过井眼中心，这种小范围的钻柱公转现象并没有形成涡动，因此，钻压的增大并没有改变近钻头段的运动状态，仅小幅扩大了其运动范围。随着转速的持续增加，近钻头段轴心运动轨迹持续扩大，并且它沿井壁爬升的距离也在增大，当转速持续增加到150 r/min时，近钻头段轴心轨迹超过了井筒轴心，钻柱绕井眼中心的公转范围较前者有较大的区别，钻柱与井壁的接触范围也在扩大，这种现象并不能称之为严格意义上的涡动，只能称之为“局部涡动”，简称“涡动”，随着钻压的增大，涡动的范围有小幅度提升。当转速持续增加到350 r/min时，近钻头段涡动范围持续增加至几近充满井眼，形成了稳定的涡动。

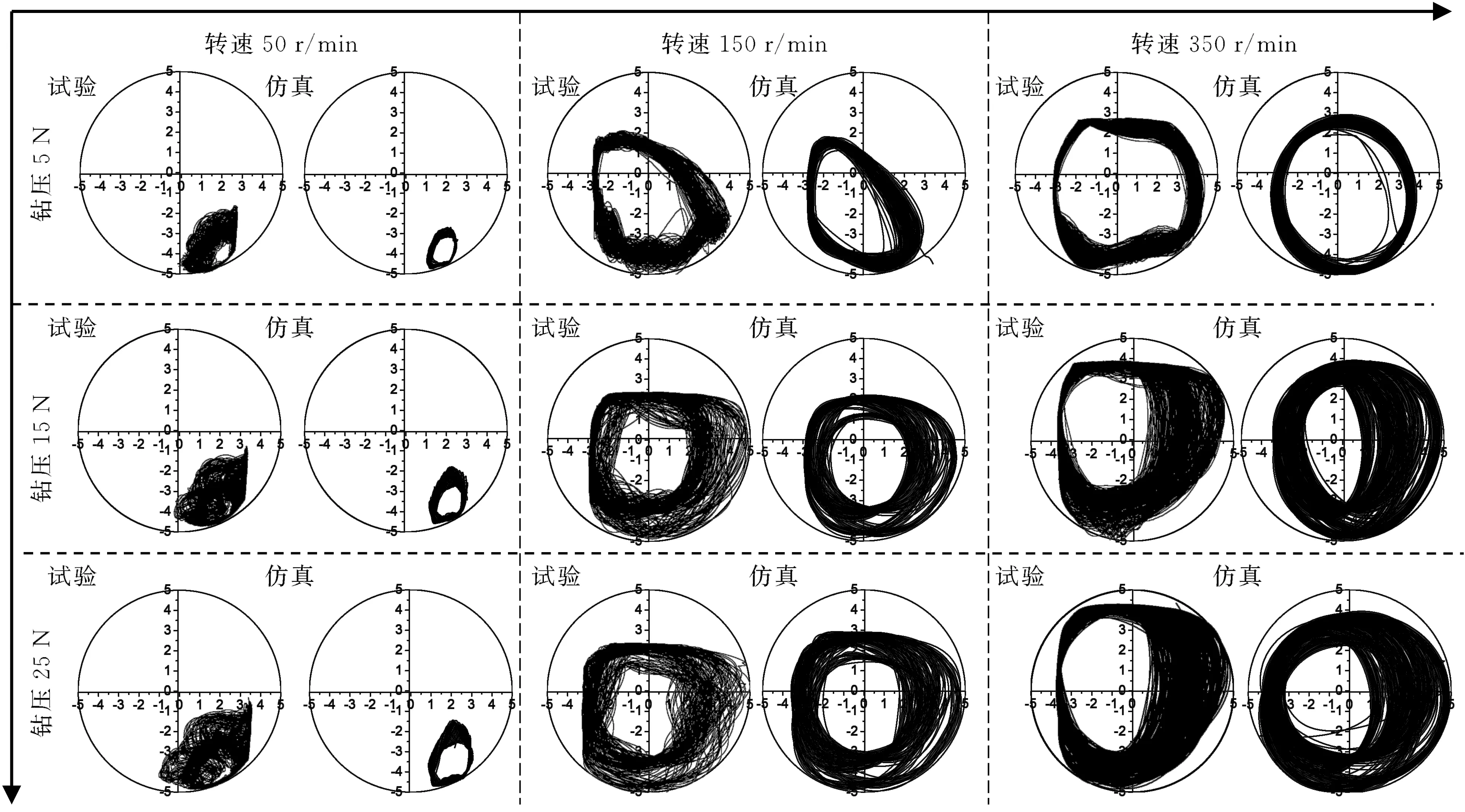
图8　不同钻压、转速下近钻头段轴心轨迹线Fig.8　Trajectory of drillstring near bit with different WOB and rotational speed

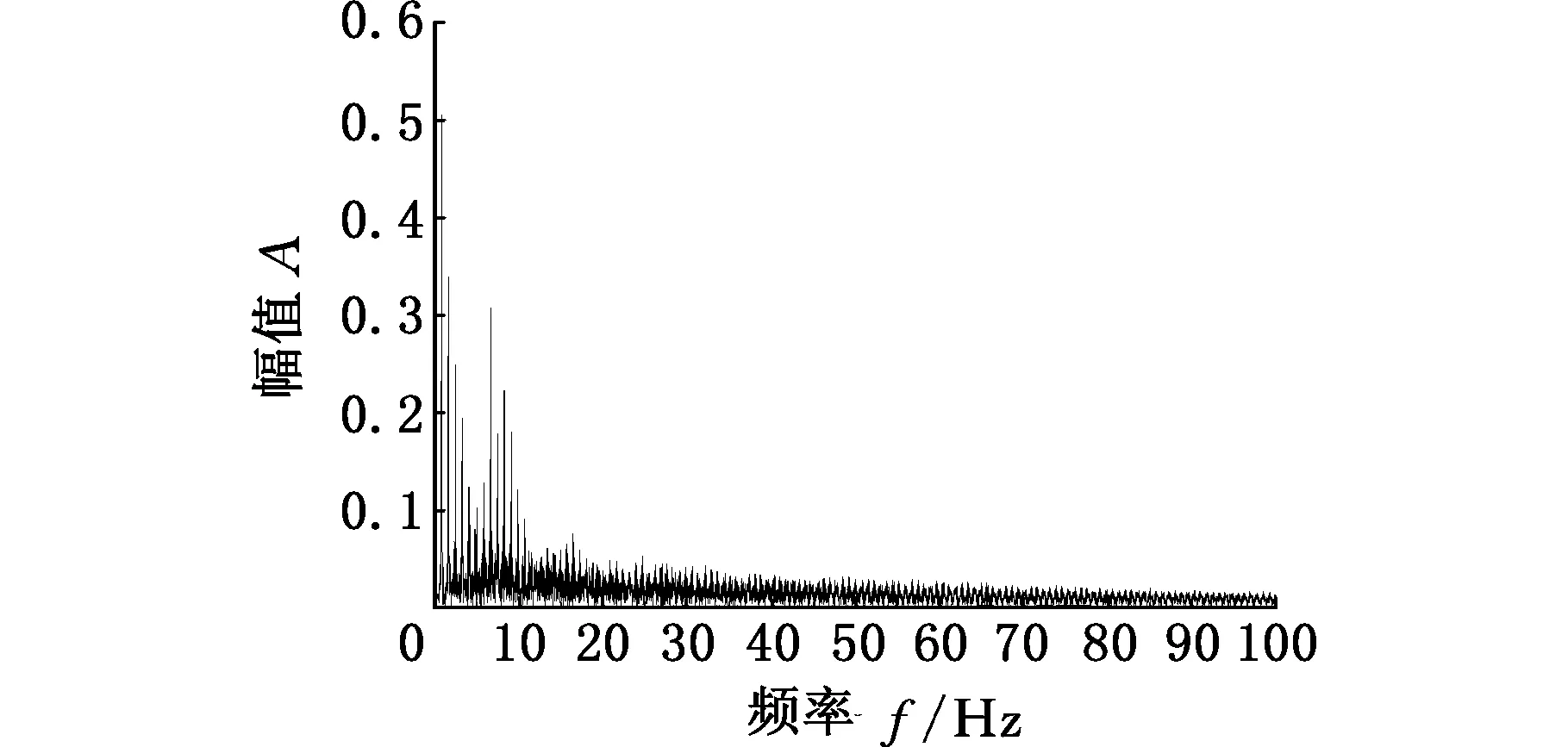
(a)转速为50 r/min

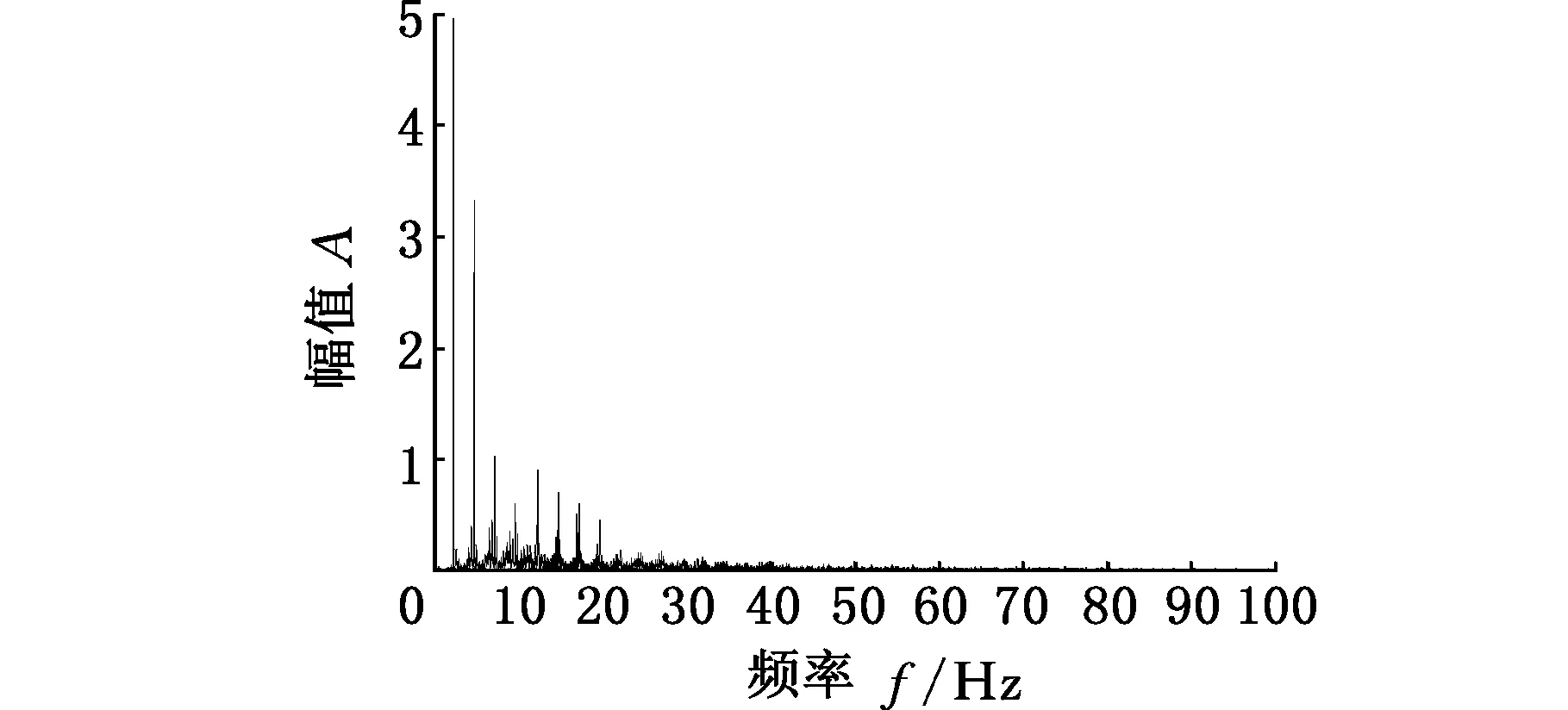
(b)转速为150 r/min

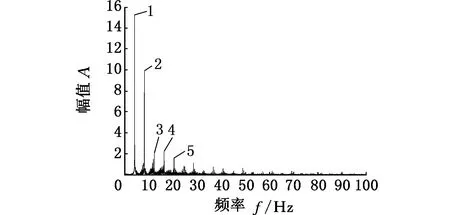
(b)转速为350 r/min图9　涡动的幅频特性Fig.9　Amplitude-frequency curve of whirling

图9所示为钻柱涡动的幅频特性曲线，该曲线是当钻压为25 N，转速为50 r/min、150 r/min、350 r/min时针对其涡动速度进行快速傅里叶变换得出的。由图9可以发现，钻柱转速为50 r/min时钻柱的幅频信号非常复杂，其振动由众多低频振动合成，这造成了钻柱运动的不稳定性，与此同时,钻柱也不会出现稳定的涡动现象；当钻柱转速提升至150 r/min时，振动杂波较图9a明显减少，这一点在图8中轴心轨迹线图中得到了反映；随着钻速持续增加到350 r/min，钻柱幅频特性曲线更加稳定，其频谱主要由5部分组成，杂波较前两种转速明显降低，这种现象同样可从图8中观察到，此时钻柱形成较为稳定的涡动。因此，可以说随着转速的增加，钻柱的涡动范围会有扩大，并且逐渐形成了稳定的涡动现象。

2.2.2转速对近钻头段钻柱涡动速度的影响

(a)转速为50 r/min

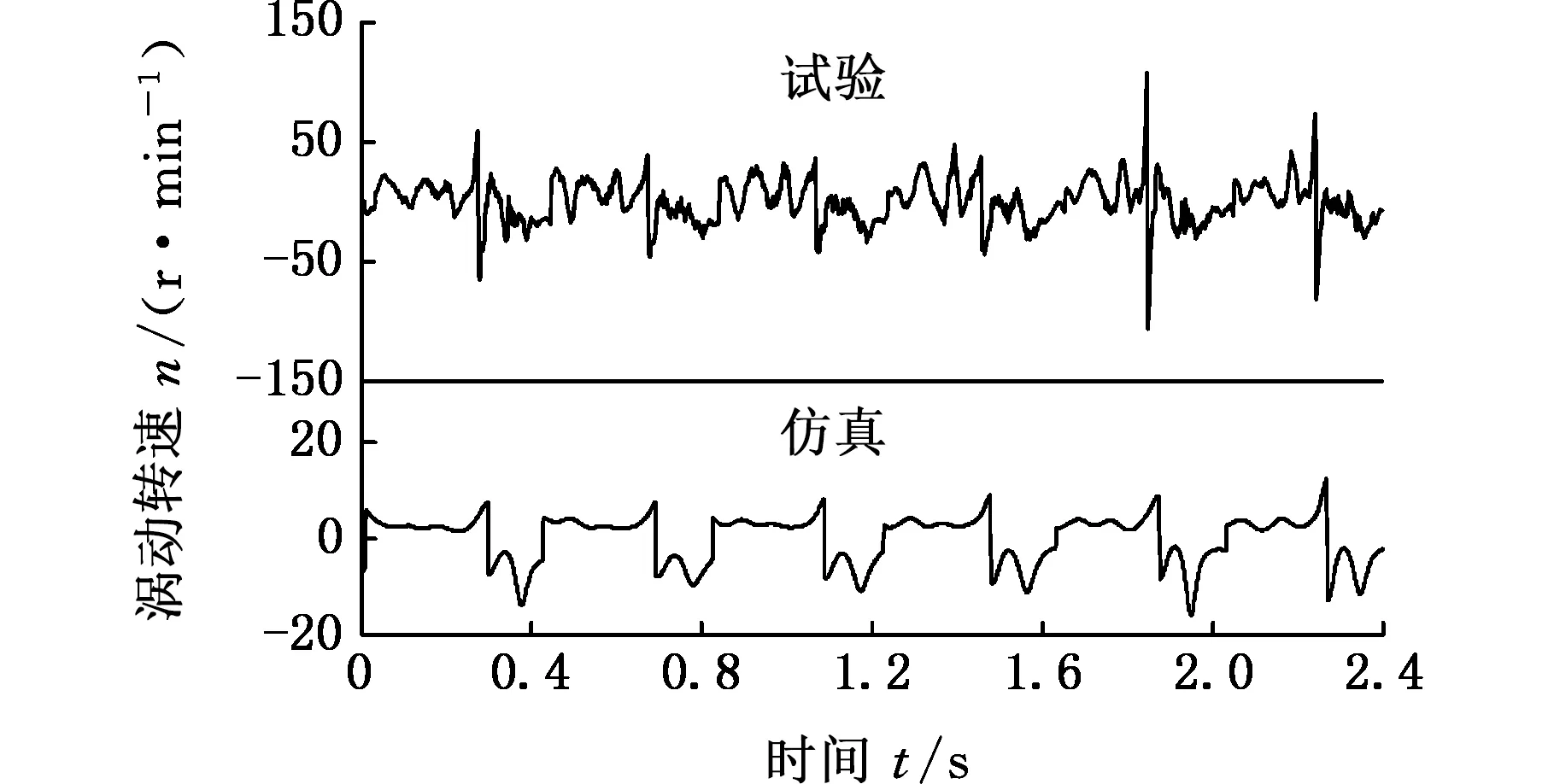
(b)转速为150 r/min

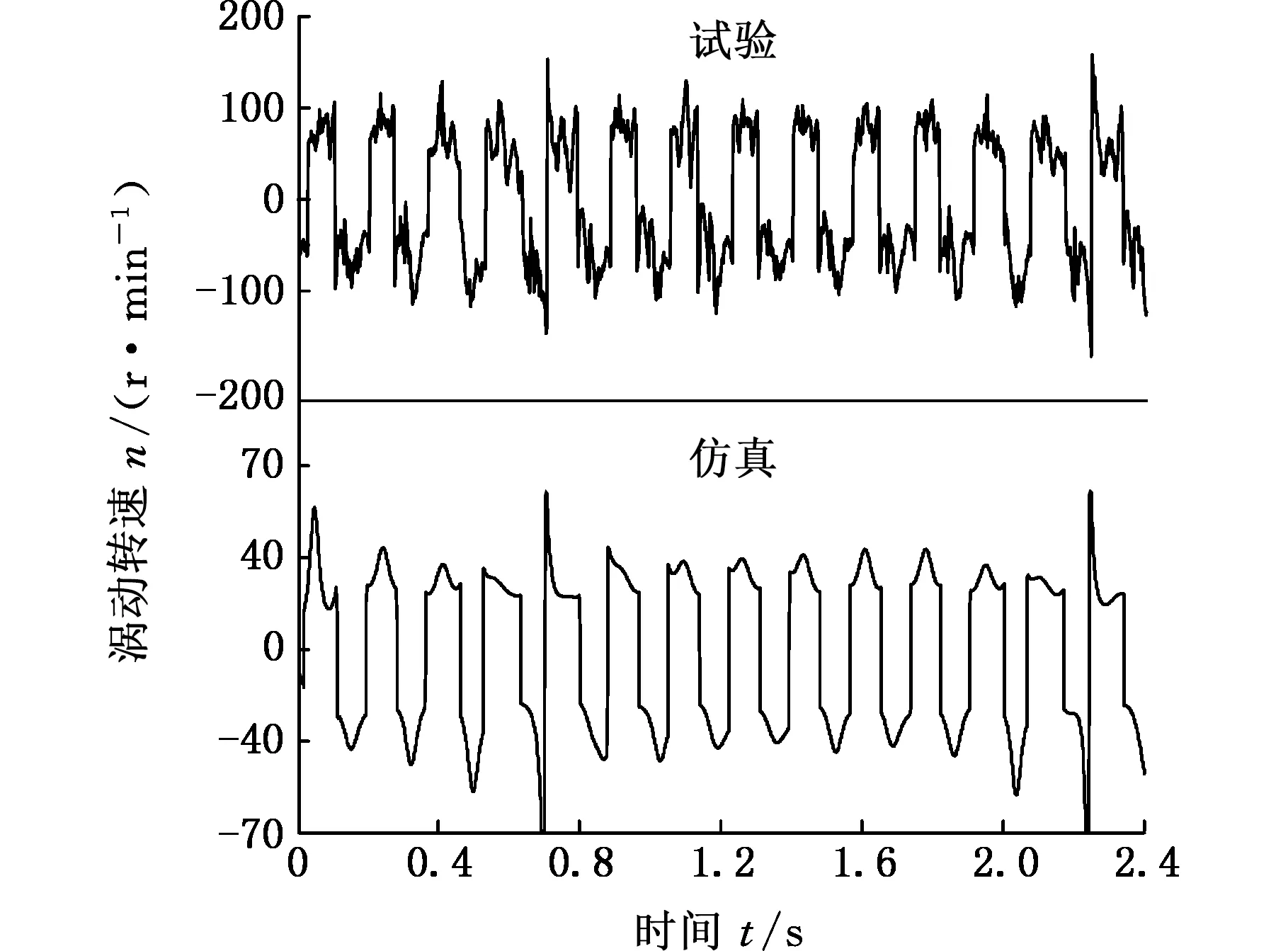
(c)转速为350 r/min图10　钻柱涡动转速曲线Fig.10　Whirl speed of drillstring near bit with different rotational speed

固定试验钻压为25 N，分别调整试验转速为50 r/min、150 r/min和350 r/min，试验和数值仿真结果如图10所示。图10显示，试验和数值仿真得到了相同的钻柱涡动特性。近钻头段钻柱既有正向涡动，同时还存在反向涡动，当试验转速为50～150 r/min时，反向涡动速度明显大于正向涡动速度，故在此转速范围内，近钻头段钻柱主要体现为反向涡动。随着转速的增加，当转速达到350 r/min时，近钻头段钻柱正反两个方向的涡动区间大体相同，其最大值达到70 r/min，数值仿真结果显示最大涡动速度为35 r/min左右，但是试验和数值仿真的涡动速度约为钻柱自转速度的0.5倍，即出现了所谓的“半频涡动”，这说明高转速下近钻头段钻柱的涡动更剧烈。

总之，在水平井钻进中，其远钻头段钻柱不会出现涡动，但当其钻速达到阈值后，水平井钻柱的近钻头段会出现稳定的涡动，并且随着转速的提升，还会出现半频涡动现象。

3　结论

(1)水平钻柱的远钻头段不会出现涡动现象，但是，当转速达到阈值后,近钻头段会出现涡动，随着转速和钻压的增大，涡动范围也会增大，涡动的幅频特性也随着转速的增加而更加清晰，钻柱涡动更加稳定、频谱组成更加单一，且其涡动频率也会随之增大，但是涡动方向并非始终如一，正反向涡动会交替出现，当转速增大大到某一阈值时还会出现“半频涡动”。

(2)钻压和转速的增大都会使钻柱和井筒的接触增多，沿井壁爬行的距离增大，并且钻柱轴心轨迹范围也会扩大。

(3)钻井液的存在会使钻柱的运动趋于稳定，随着钻井液流速的增加，钻柱的运动范围也在逐渐扩大，但是钻井液的存在及其流速的变化并不会改变钻柱现有的运动状态。

参考文献：

[1]JANSEN J D. Non-linear Rotor Dynamics as Applied to Oil-well Drill String Vibration[J]. Journal of Sound and Vibration, 1991, 147(1): 115-135.

[2]JANSEN J D. Whirl and Chaotic Motion of Stabilized Drill Collars[J]. SPE Drilling Engineering,1992,7(2):107- 114.

[3]NAGANAWA S, SATO R, ISHIKAWA M. Cuttings-transport Simulation Combined with Large-scale-flow-loop Experimental Results and Logging-while-drilling Data for Hole-cleaning Evaluation in Directional Drilling [J]. SPE Drilling & Completion, 2017, 17(40):1-14.

[4]CHRISTOFOROU A P, YIGIT A S. Dynamic Modeling of Rotating Drillstrings with Borehole Interaction[J]. Journal of Sound and Vibration,1997,206(2):243-260.

[5]DYKSTRA M W, CHEN D C, WARREN T M. Experimental Evaluations of Drill Bit and Drill String Dynamics[C]//SPE Annual Technical Conference and Exhibition.New Orleans,1994:319-334.

[6]KHULIEF Y A, AL-SULAIMAN F A,BASHMAL S.Vibration Analysis of Drillstrings with Self-excited Stick-slip Oscillations[J]. Journal of Sound and Vibration, 2007, 299(3):540-558.

[7]HAYAT M, ALAIN B, GUY F. A Nonlinear Well-drillstring Interaction Model [J]. Journal Vibration and Acoustics, 2003, 125(1): 46-52.

[8]肖文生,张扬,钟毅芳. 钻柱在钻井液和井壁摩阻共同作用下的涡动[J].中国机械工程,2004,15(4):54-58.

XIAO Wensheng, ZHANG Yang, ZHONG Yifang. Whirl Motion of Drill String under the Combined Action of Drilling Fluid and Borehole Friction[J].China Mechanical Engineering，2004,15(4):54-58.

[9]姚永汉,狄勤丰,朱卫平,等. 底部钻具组合的涡动特征分析[J]. 石油钻探技术,2010,38(4):84-88.

YAO Yonghan, DI Qinfeng, ZHU Weiping, et al. Analysis of Whirl Properties of Bottom Hole Assembly[J].Petroleum Drilling Techniques, 2010,38(4):84-88.

[10]狄勤丰,王文昌,姚永汉,等. 底部钻具组合动力学模型及涡动特性仿真[J]. 中国石油大学学报(自然科学版),2010,34(3):53-56.

DI Qinfeng, WANG Wenchang, YAO Yonghan, et al. Dynamic Model of Bottom Hole Assembly and Simulation of Vortex Characteristics[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010,34(3):53-56.

[11]马汝涛,纪友哲,贾涛, 等. 底部钻具规则涡动轨迹的内摆线描述方法[J]. 中国石油大学学报(自然科学版),2011,35(3):76-78.

MA Rutao, JI Youzhe, JIA Tao, et al. A Method for Describing the Whirl Trajectory of Bottom Drilling Tools[J]. Journal of China University of Petroleum(Edition of Natural Science), 2011,35(3):76-78.

[12]张晋凯,李根生,黄中伟，等. 涡动钻柱内赫巴流体的流动特性研究[J]. 石油钻探技术,2013 (5):82-88.

ZHANG Jinkai, LI Gensheng, HUANG Zhongwei, et al. Study on the Flow Neiheba Fluid Eddy Characteristics of the Whirling Drill String [J]. Petroleum Drilling Techniques, 2013 (5):82-88.

[13]张晋凯,李根生,黄中伟，等. 不同偏心度的环空涡动流场特性[J].石油钻采工艺,2016，38(2):133-137.

ZHANG Jinkai, LI Gensheng, HUANG Zhongwei, et al. Characteristics of Annular Whirl Flow Field with Different Eccentricity[J]. Oil Drilling & Production Technology, 2016，38(2):133-137.

[14]史玉才. 下部钻柱涡动规律研究[C]//中国土木工程学会.科技、工程与经济社会协调发展——中国科协第五届青年学术年会.上海, 2004:1-10.

SHI Yucai. Study on Whirl Motion of Bottom Drill String[C]//Chinese Woodworker Cheng Society. Harmonious Development of Science and Technology, Engineering and Economy and Society—Proceedings of the Fifth Youth Academic Annual Conference of China Association for Science and Technology.Shanghai, 2004:1-10.

[15]李子丰. 钻柱涡动理论研究的必由之路——钻井液动力润滑学与钻柱动力学相结合[J]. 石油学报,2013,34(3):607-610.

LI Zifeng. An Inevitable Way in Drill-string Whirling Research: Combination of Drilling Fluid Power Lubrication with Drill String Dynamics[J]. ACTA Petrolei Sinica, 2013，34(3):607-610.

[16]ROBNETT E W, HOOK J A, HEISIG J D,et al. Analysis of the Stick-slip Phenomenon Using Downhole Drillstring Rotation Data[C]//Proceedings of the IADC/ SPE Asia Pacific Drilling Technology Conference(APDT).Amsterdam, 1999:1-10.

[17]张文.转子动力学理论基础[M].北京:科学出版社, 1990：38-41.

ZHANG Wen. Fundamentals of Rotor Dynamics[M]. Beijing: Science Press, 1990:38-41.

[18]阎铁, 迟立斌, 毕雪亮. 基于钻柱内外钻井液流速影响的横向振动频率模型[J].科学技术与工程，2014,14(1): 1671-1815.

YAN Tie, CHI Libin, BI Xueliang. Model of Drilling String Lateral Vibration Frequence under the Influence of Drilling Fluid Flow Frequence under the Influence of Drilling Fluid Flow Velocity Inside and Ouside of the Drill String[J]. Science Technology and Engineering, 2014, 14(1):1671- 1815.

(编辑陈勇)