平面四杆机构刚体导引综合的小波特征参数法

孙建伟　王　鹏　刘文瑞　褚金奎

1.长春工业大学机电工程学院,长春,1300122.大连理工大学精密与特种加工教育部重点实验室,大连,116023

0　引言

机构尺度综合的本质是设计出能够满足预期函数要求、轨迹要求或刚体导引要求的机构，包括三个方面：函数综合、轨迹综合和刚体导引综合。机构的刚体导引综合比另两种尺度综合更困难，因为刚体导引综合不仅要求其刚体转角满足给定的转角函数，而且同时要求其刚体位置满足给定的点位位置。刚体导引综合作为四杆机构设计的一个重要的方面，在实际的工程应用中有着重要意义。国内外许多学者已经提出多种解决连杆机构刚体导引综合问题的方法[1-6]。图谱法是一种必要的尺度综合方法[7],HRONES等[8]建立了包含10 000个四杆机构的图谱。随着计算机网络技术的发展，数值图谱法逐渐取代了效率和精度不足的传统曲线图谱法。王知行等[9]利用数值图谱法对平面四杆机构综合数值比较法进行了研究。PANG等[10]、MULLINEUX[11]利用数值图谱法分别对平面和空间机构尺度综合进行了分析。孙建伟等[12-13]基于数值图谱法理论对RCCC机构的函数综合和轨迹综合进行了深入研究。

傅里叶级数法在数值图谱中对整周期的尺度综合较为普遍，文献[14]首次提出将傅里叶级数理论用于平面连杆机构的综合问题。文献[15]利用快速傅里叶变换对平面四杆机构连杆曲线进行了综合。文献[16]利用傅里叶级数对平面刚体导引综合问题进行了研究。然而，由于傅里叶级数只能保证结果在整个周期上对给定设计条件进行逼近，无法保证给定的设计区间的设计精度，而多数情况下，对某一特定区间进行设计更加符合实际需求[17-18]。小波函数在时域和频域上都具有较好的解析能力，因此，对非整周期设计条件下的尺度综合问题具有独特的优势[19-20]。

本文基于数值图谱法的基本思想和小波级数理论，根据文献[21-22]研究非整周期函数、轨迹的成果，提出了基于小波级数进行平面四杆机构非整周期刚体导引输出特征提取方法，并建立了相应的四杆机构刚体导引输出特征参数数据库，利用建立的数据库、模糊识别理论和给出的理论公式，达到实现平面四杆机构非整周期给定设计区间的刚体导引综合的目的。

1　连杆转角函数与刚体转角函数的关系

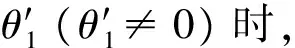
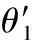
(1)

式中，θt(θt=ωt) 为运动时刻t的函数,ω为角速度。

图1　刚体导引机构示意图Fig.1　Diagram of motion generation mechanism

当曲柄旋转的时候，复平面上由P、Q两点生成的连杆曲线如下：

rP(θ1)=Lβeiβ+L1ei(θ1+θ4)+LPei(θP+θ2+θ4)

(2)

rQ(θ1)=Lβeiβ+L1ei(θ1+θ4)+LQei(θQ+θ2+θ4)

(3)

连杆CD上的标线PQ可以表示为

PQ(θ1)=rQ(θ1)-rP(θ1)=
(LQei(θQ+θ4)-LPei(θP+θ4))eiθ2

(4)

式(4)即为带有预定时标的平面四杆刚体导引生成的基本公式。由该式可以看出，四杆机构的刚体导引的位置生成函数取决于连杆转角函数，而机构的连杆转角又由机构的基本尺寸型决定。也就是说，带有预定时标刚体导引机构的位置转角函数由机构的基本尺寸型决定。矢量LQei(θQ+θ4)-LPei(θP+θ4)只影响运动刚体的点位，它由与基本尺寸型相对应的实际机构和连杆的标线位置所决定，这就确定了带有预定时标刚体导引转角函数与连杆转角函数之间的关系。

由图1可知：

(5)

由式(5)可得

γ(θ1)=θ2(θ1)+

(6)

令

则式(6)可写为

γ(θ1)=θ2(θ1)+K

(7)

2　刚体转角输出的小波分析

根据文献[21]可知，在小波分析过程中有尺度函数φ和小波函数ψ，分别表示如下：

(8)

(9)

已知任意连续函数都可以由φ(2jθt)函数表示，四杆机构输出的小波分析可以描述为[23]

(10)

式中，j为小波分解级数；y(0)为小波平均数；w(n,l)为第n级第l个小波细节数。

小波平均数和全部细节数构成了小波系数，根据以上分析可知，连杆转角函数θ2经过小波变换可表示为

(11)

θ2(2j))φ(θt/θ)

(12)

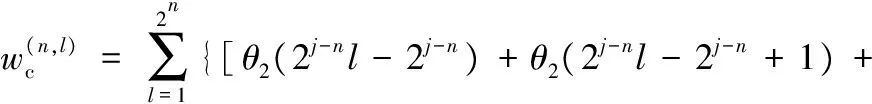
2j-n)+…+θ2(2j-nl-1)]/2j-n}ψ(2nθ0/θ-l+1)

(13)

式中，θ2(1),θ2(2),θ2(3),…,θ2(2j)为连杆转角函数采样点，θ为设计区间。

类似地，刚体转角输出函数γ由小波变换可表述为

(14)

(15)

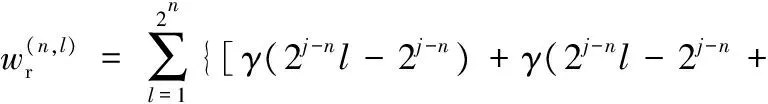
2j-n)+…+γ(2j-nl-1)]/2j-n}ψ(2nθt/θ-l+1)

(16)

式中，γ(1),γ(2),γ(3), …,γ(2j)为刚体转角采样点。

由式(7)可知：

γ(m)=θ2(m)+K

(17)

m=1,2,…,2j-nl-1

将式(17)代入式(15)和式(16)中有

(18)

(19)

根据式(18)、式(19)可知，机构相同基本尺寸型的刚体转角和连杆转角的小波细节数相等，其小波平均数相差参数K(K是由LP、LQ、θP、θQ、θ4决定的)，因此刚体转角输出的特征可以由式(19)连杆转角的小波细节数决定。而对于四杆机构，连杆转角由四杆机构的四根杆长L1、L2、L3、L4决定，所以定义L1、L2、L3、L4为机构的基本尺寸型。

图2　扫描图Fig.2　Scanning steps

3　平面四杆刚体导引综合方法

3.1　建立基本尺寸型数据库及模糊识别

(20)

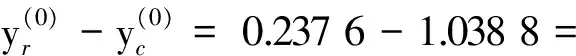
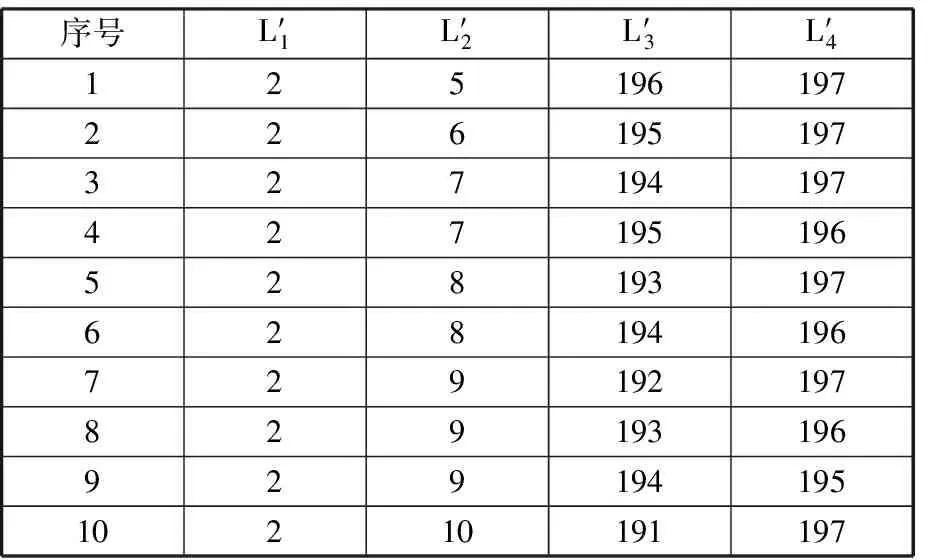
表1　数据库中的10组基本尺寸型Tab.1　10 sets of the MBDT in the database

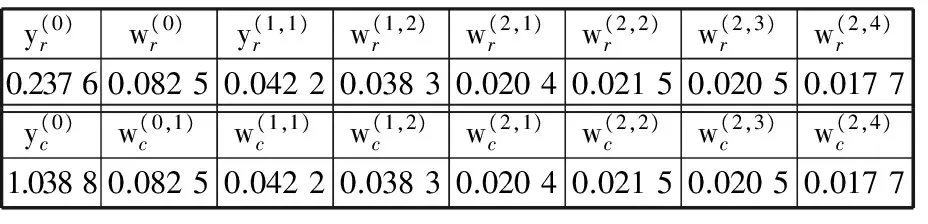
表2　刚体转角和相应的连杆转角的小波系数Tab.2　The wavelet coefficients of the RBRA and the corresponding CRRA

3.2　计算实际尺寸及安装位置参数

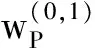
(21)

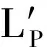
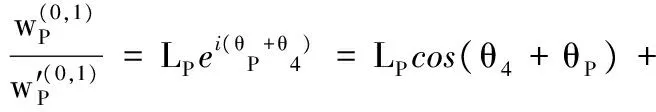
(22)

式(22)由实部和虚部构成，并且LP、θP、θ4可以写成：

(23)

(24)

由基本尺寸型所生成的刚体位置的小波平均数如下：

(25)

类似地，由目标机构所生成的刚体位置的小波平均数如下：

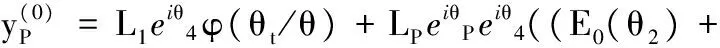
(26)

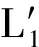
((E0(θ2)+E1(θ2)+…+E2j-1(θ2))2-jφ(θt/θ)=

代入式(26)中，有

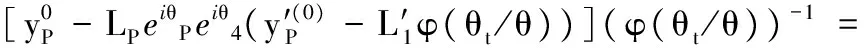
(27)

(28)

(29)

将θ4代入式(24)可求出θP，将L1、θ4、LP、θP代入式(2)中得

rP(θ1)-L1ei(θ1+θ4)-LPei(θP+θ2+θ4)=Lβeiβ

(30)

通过选定图1中刚体预定位置的P点作为参考点，将这个点和相应的θ1和θ2的值代入式(30)中，目标机构的机架位置可由下式求出：

Lβ={[Re(rP(θ1)-L1ei(θ1+θ4)-LPei(θP+θ2+θ4))]2+

(31)

β=arctan((Im(rP(θ1)-L1ei(θ1+θ4)-LPei(θP+θ2+θ4)))2/
(Re(rP(θ1)-L1ei(θ1+θ4)-LPei(θP+θ2+θ4)))2)

(32)

3.3　平面四杆刚体导引综合步骤

当机构基本尺寸型的转角满足刚体转角的设计要求时，机构位置可以通过分析文献[22]中小波特征参数来得到。因此，平面四杆机构刚体导引的综合可以由以下步骤实现(图3)。

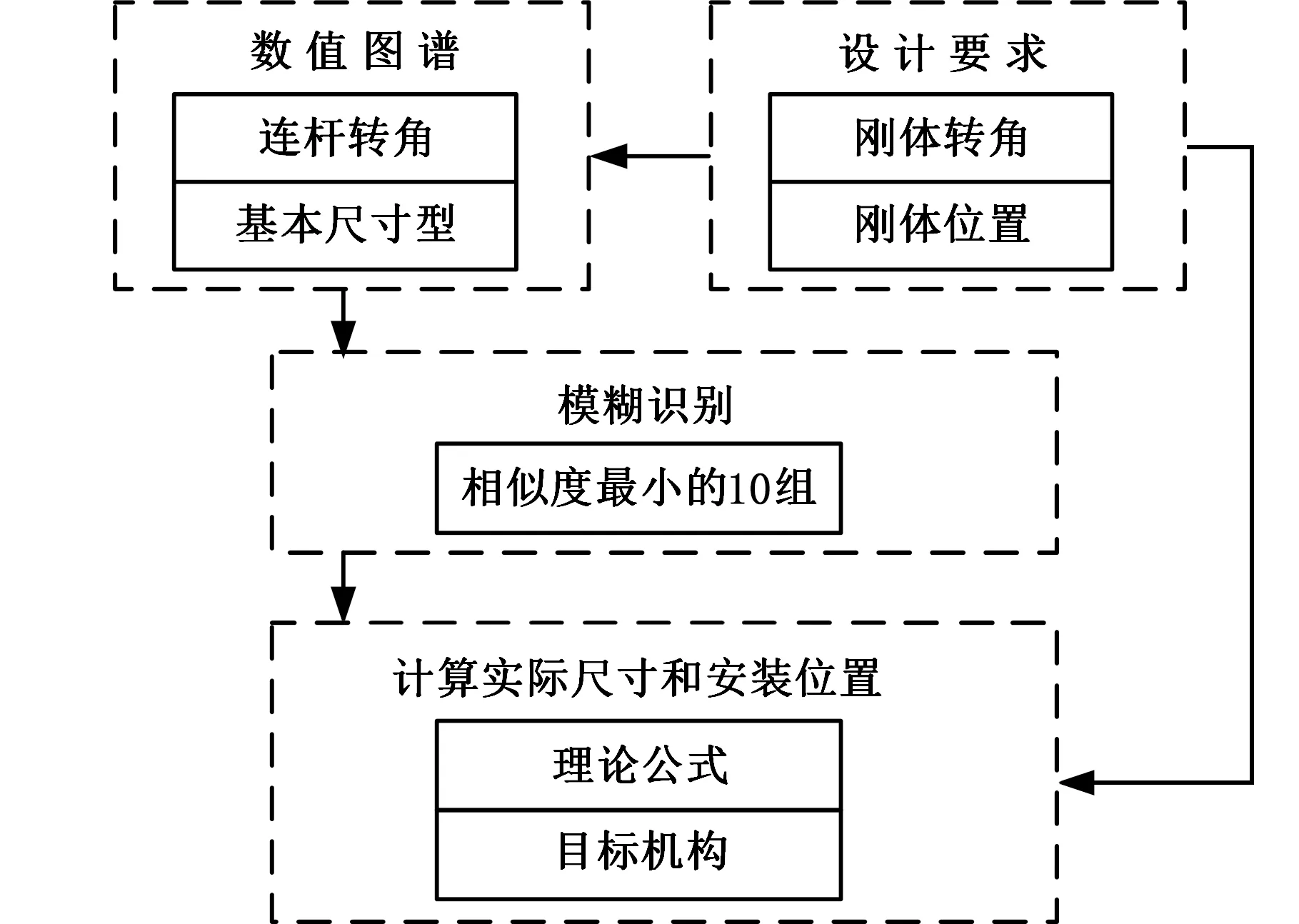
图3　平面四杆刚体导引综合流程图Fig.3　Flow chart of planar four-bar motion generation synthesis

(1)根据所要求的刚体转角和由机构基本尺寸型所决定的连杆转角的小波系数之间的关系，建立一个关于转角输出特征参数的数值图谱数据库。

(2)通过对给定刚体转角进行采样，并对其进行Haar小波变换，得到转角小波系数。

(3)在数值图谱库里对步骤(2)中得到的转角特征参数和相应小波参数进行识别。利用模糊识别的方法，从中得到满足要求的若干组机构基本尺寸型。

(4)将位置问题转换成刚体轨迹综合问题，将步骤(3)中识别出的基本尺寸型与给定的带有预定时标的曲线进行轨迹综合。

(5)利用式(21)～式(32)，机构的实际尺寸和安装位置可以全部得出。

4　综合算例

4.1　理论算例

为验证上述方法理论及公式推导的正确性，本文首先建立了包含101 408组平面四杆机构的基本尺寸型数据库，在数据库中任选一组基本尺寸型为目标机构。本文选取基本尺寸型数据库中第66 077组基本尺寸型：L1=30 mm,L2=100 mm,L3=114 mm,L4=156 mm,安装位置为LP=10 mm,LQ=25 mm,θP=π/4,θQ=π/9,Lβ=10 mm,β=π/4,θ4=π/6，输入角θ1∈[30°, 120°]。选取小波分解级数j=4。利用3.3节的步骤即可进行带有预定时标四杆机构刚体导引的尺度综合。表3所示为通过模糊识别确定的10组机构基本尺寸型。

表4所示为综合出的机构实际尺寸和安装位置等参数。图4所示为综合出的机构刚体导引标线与给定刚体导引标线的拟合比较(给出了2组机构刚体导引标线的拟合图)，其中实线代表给定的刚体导引标线，虚线代表综合所得机构生成的刚体导引标线。从图4中可以看出，第2组为相近的基本尺寸型生成的刚体标线与原标线的拟合，效果相当理想，而第5组识别出的为目标机构的基本尺寸型生成的标线，并与原标线完全重合，即验证了理论公式的正确性和本文方法的有效性。

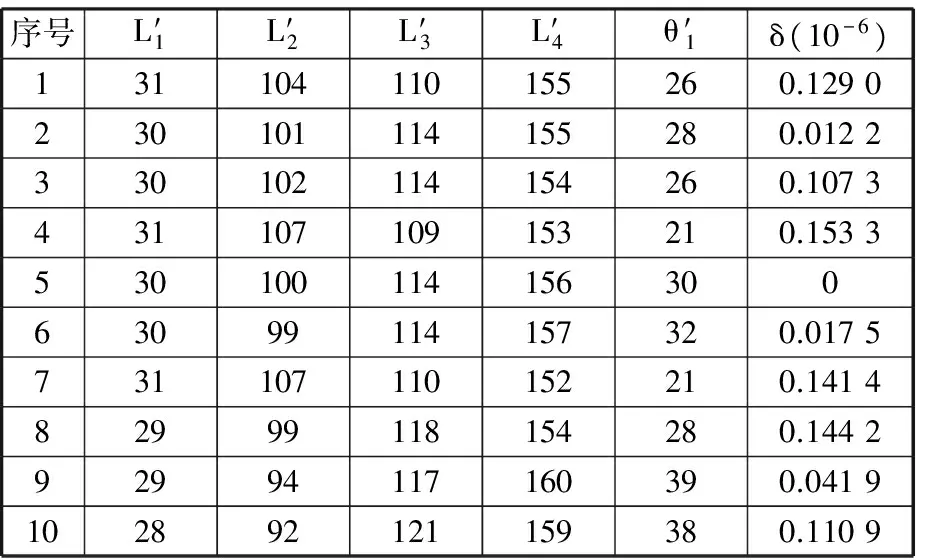
表3　综合结果Tab.3　Synthesized results

表4　机构实际尺寸和安装位置参数Tab.4　Parameters of the actual size and installing positions

4.2　实际算例

为生产装配线设计一个输送工件的铰链四杆机构，如图5所示，标线1-1为要求输送工件的起始位置，标线2-2为输送工件的完成位置。轨迹1-2为P点所经历的预定位置。要求被输送的工件的转角和位置满足：

γ=0.9θ1-261°px=29cosθ1py=48sinθ1

θ1∈[290°,320°]

式中，θ1为曲柄转角；γ为刚体转角，是关于输入角的函数；px为P点横坐标；py为P点纵坐标。

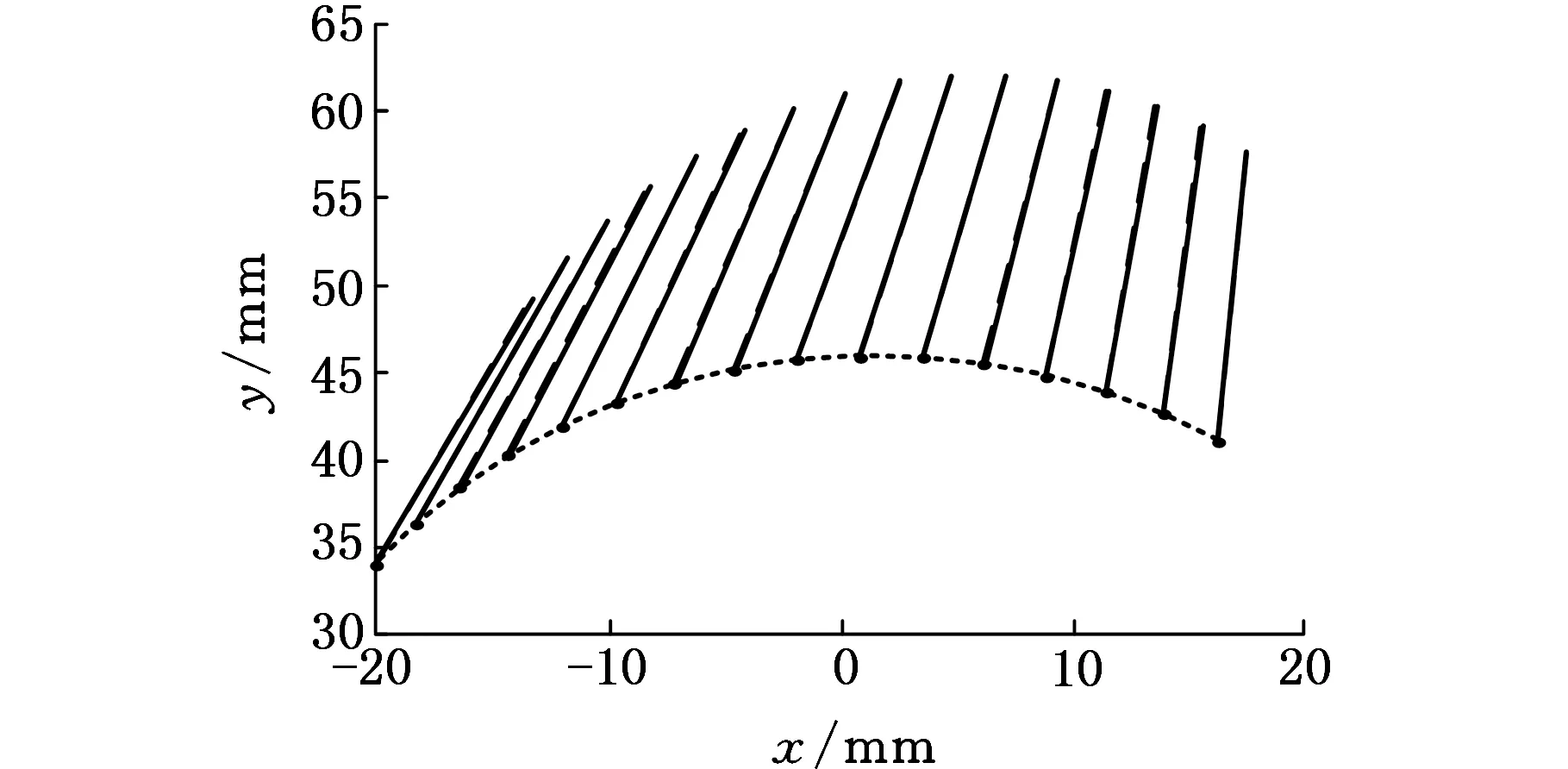
(a)第2组

(b)第5组

图5　设计示意图Fig.5　Design schematic

图4　机构生成的标线与给定刚体标线的拟合Fig.4　Fitting of the prescribed guidance-line and generated guidance-line

根据前面给出的步骤进行设计。

(1)建立了含有101 408组基本尺寸型的刚体转角的数值图谱数据库。

(2)计算刚体转角函数的前8个小波系数，列于表5中。

(3)经过模糊识别选取的10组机构基本尺寸型和相应的相似度δ列于表6。

表5　平面四杆机构刚体转角的小波系数Tab.5　Wavelet coefficients of RBRA function of planar four-bar mechanism

(4)在刚体导引标线上选取P点位置的前8个小波系数列于表7中。

(5)通过理论计算公式确定的机构实际尺寸、标线位置(P点位置)、曲柄起始位置和机构安装尺寸参数列于表8。所要求的刚体转角和刚体位置以及机构基本尺寸型生成的刚体转角和刚体位置拟合的程度如图6所示，所产生的转角误差和位置误差如图7和图8所示。由图6可以看出，逼近程度相当理想，即用本方法确定的机构可以较好地实现带有预定时标刚体导引的尺度综合，并可以给出多个机构的设计方案。

表6识别出的基本尺寸型和相应的相似度
Tab.6IdentifiedMBDTandthecorrespondingsimilarities

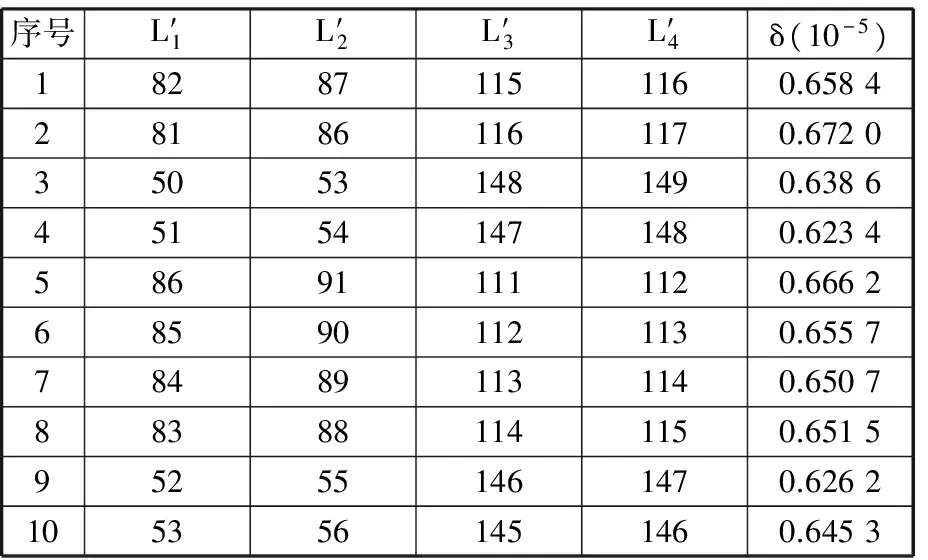
序号L′1L′2L′3L′4δ(10-5)182871151160．6584281861161170．6720350531481490．6386451541471480．6234586911111120．6662685901121130．6557784891131140．6507883881141150．6515952551461470．62621053561451460．6453

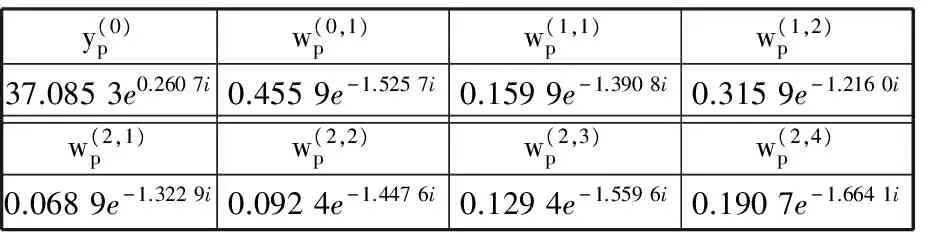
表7　预定位置的小波系数Tab.7　Wavelet coefficients of the prescribed position

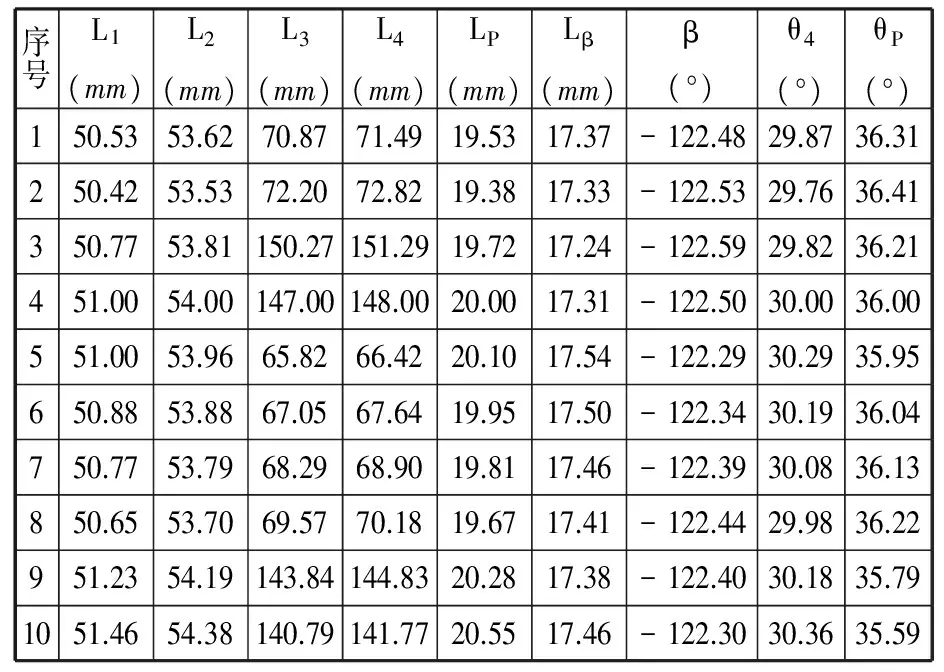
表8　综合机构实际尺寸及安装位置参数Tab.8　Actual sizes and installation positions of the synthesized mechanism

5　结论

(1)本文建立了平面四杆机构刚体导引的数学模型，通过对刚体转角输出和其对应连杆转角输出小波变换的分析，发现了小波系数之间的关系。根据这一关系建立了包含101 408组基本尺寸型的平面四杆机构刚体导引输出特征参数数据库。

(2)利用模糊识别理论识别出与给定的刚体转角相对应的连杆转角的基本尺寸型，将刚体位置转化为轨迹综合问题，给出了计算机构实际尺寸及实际安装位置的理论公式，从而实现了平面四杆机构的非整周期刚体导引综合问题的求解。

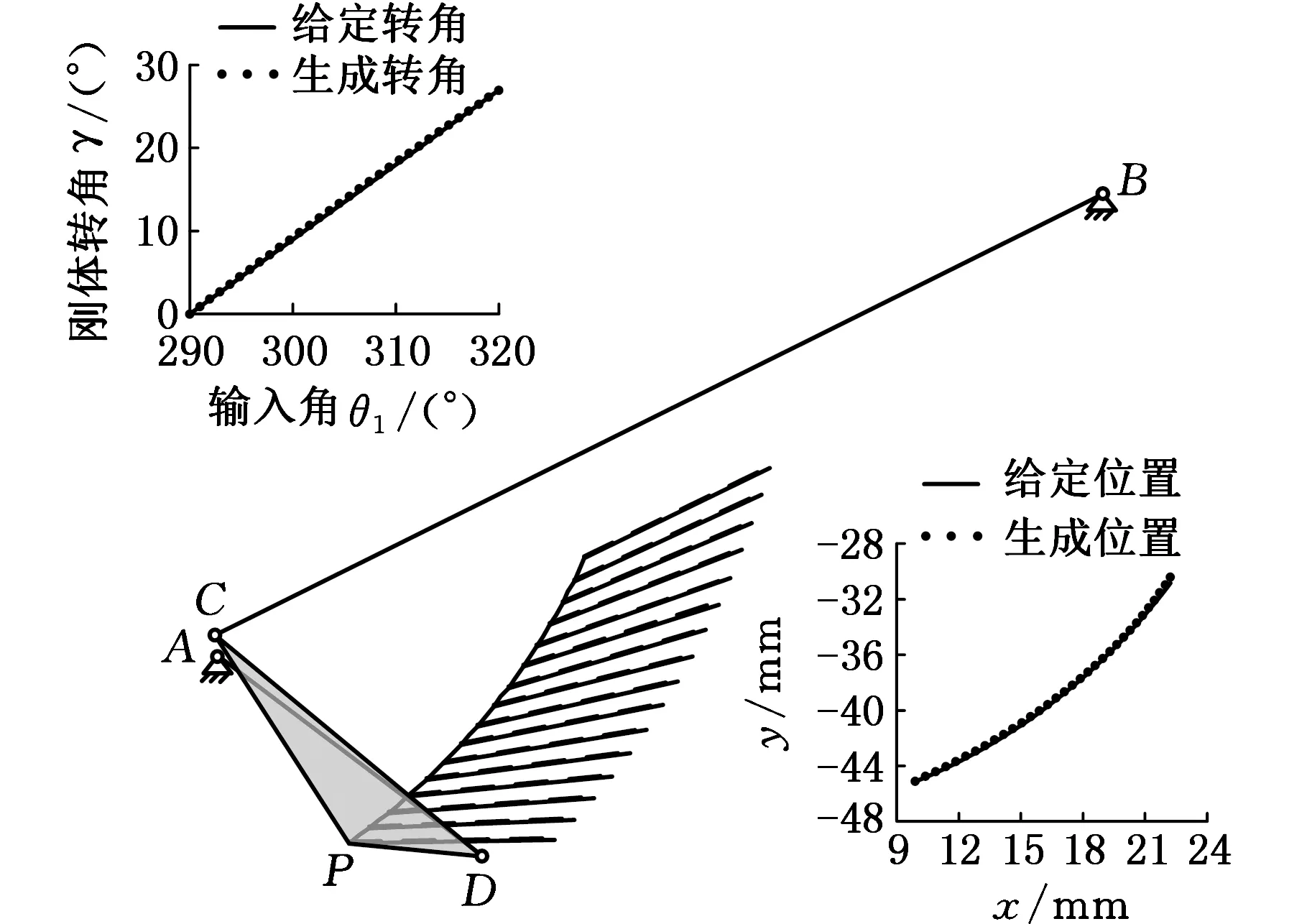
(a)第3组拟合

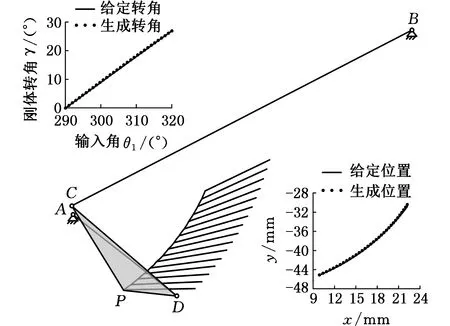
(b)第4组拟合图6　刚体转角和刚体位置拟合图Fig.6　Fitting graphs of motion rotation angle and motion position

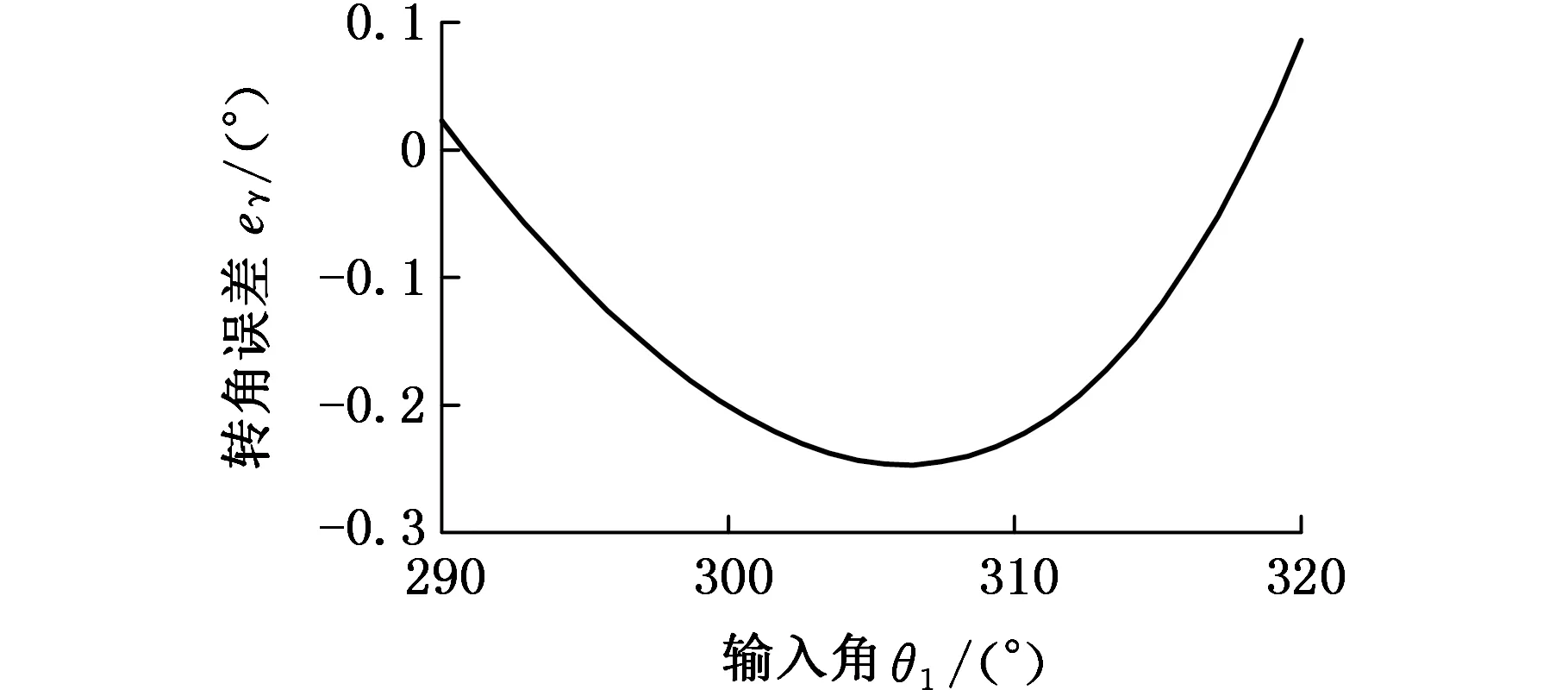
(a)第3组转角误差

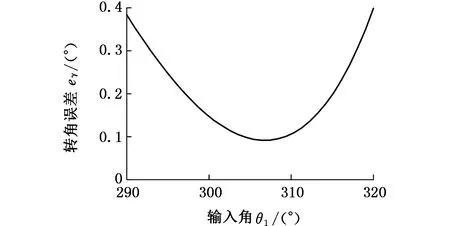
(b)第4组转角误差图7　转角误差Fig.7　Rotation angle errors

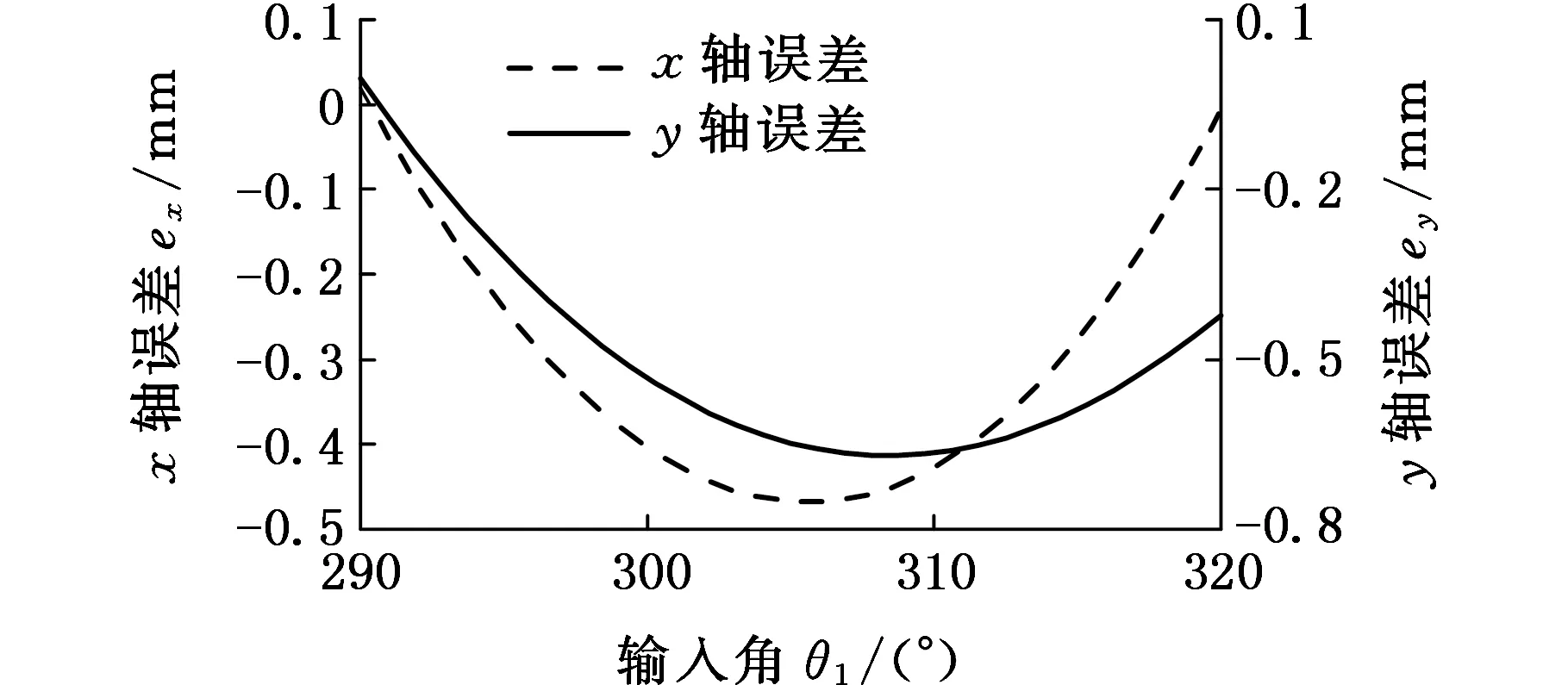
(a)第3组位置误差

(b)第4组位置误差图8　位置误差Fig.8　Position errors

(3)本文提出的方法在解析几何算法的精度和图谱法的计算方面上有优势，而且避免了非线性方程的求解以及克服了傅里叶级数不能很好地描述非整周期机构刚体导引的缺点；同时，可以根据刚体导引生成要求给出多组可供设计者选择的综合结果。

参考文献：

[1]吴鑫,褚金奎,曹惟庆.带有预定时标平面四杆刚体导引机构尺度综合的研究[J]. 机械工程学报, 1999, 35(5): 106-110.

WU Xin, CHU Jinkui, CAO Weiqing. Study on Dimensional Synthesis of Planar Linkages for Rigid-body Guidance with Prescribed Timing[J]. Chinese Journal of Mechanical Engineering, 1999, 35(5): 106-110.

[2]WANG Z X, YU H Y , TANG D W, et al. Study on Rigid-body Guidance Synthesis of Planar Linkage[J]. Mechanism and Machine Theory, 2002, 37(7): 673-684.

[3]冯春, 谢进, 陈永. 利用混沌与分形进行平面机构综合[J]. 中国机械工程, 2004, 15(9):753-756.

FENG Chun, XIE Jin, CHEN Yong. Using Chaos and Fractals to Synthesis Planar Mechanism[J].China Mechanical Engineering, 2004, 15(9):753-756.

[4]孙建伟, 路贺, 褚金奎. 基于傅里叶级数的RCCC机构运动综合[J]. 中国机械工程, 2014, 25(21):2841-2847.

SUN Jianwei, LU He, CHU Jinkui. Fourier Series Method for Motion Generation of RCCC Mechanism[J].China Mechanical Engineering, 2014, 25(21):2841-2847.

[5]MYSZKA D H, MURRAY A P. Pole Arrangements that Introduce Prismatic Joints into the Design Space of Four-and Five-position Rigid-body Synthesis[J]. Mechanism and Machine Theory, 2010, 45(9): 1314-1325.

[6]ZHAO P, LI X, PURWAR A, et al. A Task-driven Unified Synthesis of Planar Four-bar and Six-bar Linkages with R-and P-joints for Five-position Realization[J]. Journal of Mechanisms and Robotics, 2016, 8(6): 061003.

[7]ALT H. Das Konstruieren von Gelenkvierecken unter Benutzung einer Kurventafel[J]. Z. VDI, 1941, 85: 69-72.

[8]HRONES J A, NELSON G L. Analysis of the Four-bar Linkage: Its Application to the Synthesis of Mechanisms[M]. New York：Press of the Massachusetts Institute of Technology，1951: 250-305.

[9]王知行, 关立文, 李建生, 等. 平面四杆机构综合数值比较法的研究[J]. 机械工程学报, 2000,36(2): 47-50.

WANG Zhixing, GUAN Liwen, LI Jiansheng, et al. Study on Numerical Comparison Method for Planar Four-bar Linkage Synthesis[J]. Journal of Mechanical Engineering, 2000, 36(2): 47-50.

[10]PANG Y, KROVI V. Fourier Methods for Synthesis of Coupled Serial Chain Mechanisms[J]. Journal of Mechanical Design, 2005, 127(2):232-241.

[11]MULLINEUX G. Atlas of Spherical Four-bar Mechanisms[J]. Mechanism and Machine Theory, 2011,46(11)：1811-1823.

[12]孙建伟,褚金奎,卫静. 利用数值图谱法进行RCCC机构的函数综合[J].中国机械工程,2008,19(6):713-717.

SUN Jianwei, CHU Jinkui, WEI Jing. Research on RCCC Mechanism Path Generation by Using Numerical Atlas Method[J].China Mechanical Engineering, 2008,19(6):713-717.

[13]褚金奎,孙建伟. RCCC 机构轨迹综合的数值图谱法[J].中国机械工程,2009,20(9):1024-1028.

CHU Jinkui, SUN Jianwei. Research on RCCC Mechanism Path Generation by Using Numerical Atlas Method[J].China Mechanical Engineering,2009,20(9):1024-1028.

[14]CAPELLEN W M Z. Kinematik und Dynamik der Kurbelschleife[J]. Werkstatt and Betrieb, 1956, 1: 581-584.

[15]褚金奎,曹惟庆. 用快速傅立叶变换进行再现平面四杆机构连杆曲线的综合[J].机械工程学报,1993,29(5): 117-122.

CHU Jinkui, CAO Weiqing. Synthesis of Coupler Curves of Planar Four-bar Linkages through Fast Fourier Transform[J] . Chinese Journal of Mechanical Engineering, 1993, 29 (5) : 117-122.

[16]LI X, WU J, GE Q J. A Fourier Descriptor-based Approach to Design Space Decomposition for Planar Motion Approximation[J]. Journal of Mechanisms and Robotics, 2016, 8(6): 064501.

[17]孙建伟, 路贺, 褚金奎. 球面四杆曲柄滑块机构函数综合的变步长数据库法[J]. 农业机械学报, 2013, 44(11): 329-335.

SUN Jianwei, LU He， CHU Jinkui. Variable Step Size Database Method for Function Generation of Spherical Four Bar Crank Slider Mechanism[J]. Transactions of the Chinese Society of Agricultural Machinery, 2013, 44(11): 329-335.

[18]孙建伟, 陈露, 褚金奎, 等. 球面四杆机构自适应数值图谱法及在收割机中的应用[J]. 农业工程学报, 2016, 32(8): 56-62.

SUN Jianwei, CHEN Lu, CHU Jinkui, et al. Adaptive Numerical Atlas Method of Spherical Four-bar Mechanism and Its Applications for Harvester[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(8): 56-62.

[19]王成志, 纪跃波, 孙道恒. 小波分析在平面四杆机构轨迹综合中的应用研究[J].机械工程学报，2004, 40(8): 34-39.

WANG Chengzhi, JI Yuebo, SUN Daoheng. Research on Applying Wavelet Analysis to Path Synthesis for Coupler Curves of Planar Four-bar Linkages[J]. Chinese Journal of Mechanical Engineering, 2004,40(8):34-39.

[21]SUN J W, LIU W R, CHU J K. Synthesis of a Non-integer Periodic Function Generator of a Four-bar Mechanism Using a Haar Wavelet[J]. Inverse Problems in Science and Engineering, 2016, 24(5): 763-784.

[22]SUN J W, LIU W R, CHU J K. Dimensional Synthesis of Open Path Generator of Four-bar Mechanism Using the Haar Wavelet[J]. Journal of Mechanical Design, 2015, 137(8): 082303.

[23]DAUBECHIES I. Ten Lectures on Wavelets[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1992:357.

(编辑王旻玥)