风轮叶片疲劳试验加载设计

傅　程　张方慧

中国船级社质量认证公司，北京，100006

0　引言

风轮叶片是风力发电机组中最关键的部件，叶片由多层玻璃纤维增强塑料铺设而成。根据叶片的受力特点和工艺限制，叶片铺层工艺中需要大量的手工作业来完成，而这必然导致质量的不稳定；另一方面，考虑到生产成本及风电机组收回成本的周期，需要叶片在至少20年的寿命周期内稳定工作，因此叶片的疲劳试验就显得非常重要。

叶片采用的玻璃纤维增强材料的疲劳性能研究与金属材料相比还很不完善；而叶片主要承受风载荷，其时变性和随机性都非常强，因此叶片的疲劳设计是将20年设计寿命作为前提，根据风载荷的统计规律模拟并折算出等效载荷及次数作为设计载荷，并进行叶片的疲劳试验。

1　叶片的基本结构及工作状态

叶片一般由玻璃纤维增强树脂铺设而成，其基本结构及铺层如图1所示。

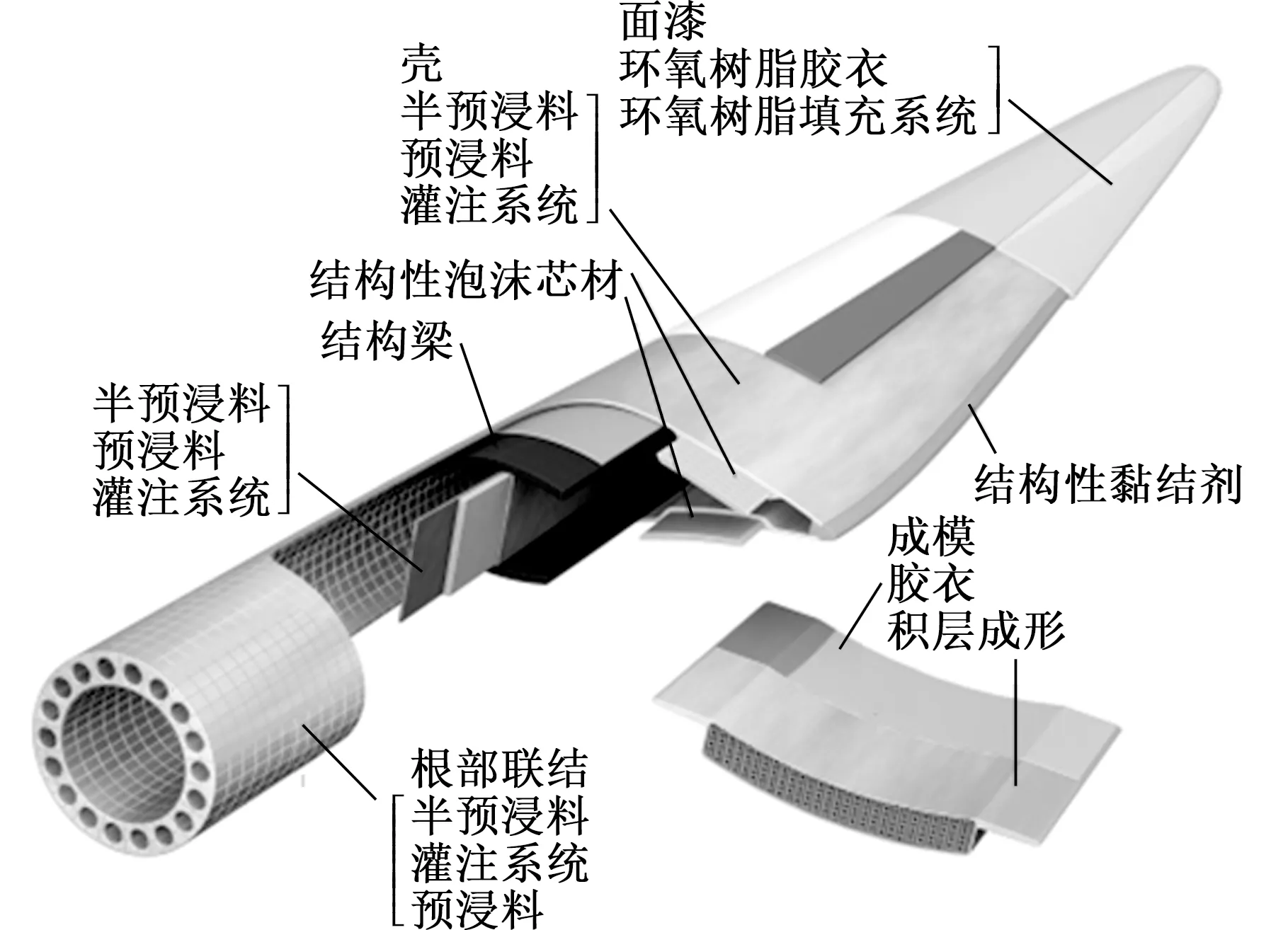
图1　叶片基本结构及铺层[1]Fig.1　Basic structure and laminate of blade[1]

叶片在工作时，叶根通过螺栓连接至轮毂，呈悬臂状安装。

基于叶片截面的复杂性，根据叶片的工作状态，一般在设计时将叶片离散成数段，每段内的截面属性是均匀的，各段的截面属性不同，根据叶片复杂的铺层情况，计算出叶片的质量分布及刚度分布等参数，作为设计叶片疲劳试验的依据。

2　叶片疲劳试验基本原理

叶片工作时主要承受空气动力产生的弯矩，为了更好地描述叶片的变形与运动，将叶片沿翼型截面厚度方向的弯曲运动称为挥舞运动，而沿弦长方向的弯曲运动称为摆振运动；叶片疲劳试验的目的就是考验叶片在挥舞弯矩和摆振弯矩下的疲劳性能。

叶片具有尺寸大、质量大、变形大的特点，循环次数在数百万次以上，采用一般的疲劳试验方法所需的激振能量大，因此目前的疲劳试验一般都采取共振法激励。激振的方式主要有电机偏心块式和液压作动筒式，目的都是为了激起叶片挥舞或摆振方向的共振，来达到振动加载的目的。

通常叶片疲劳试验的试验装置如图2所示，试验中采用电机带动偏心质量块激励的方式施加交变载荷，达到激励的目的。

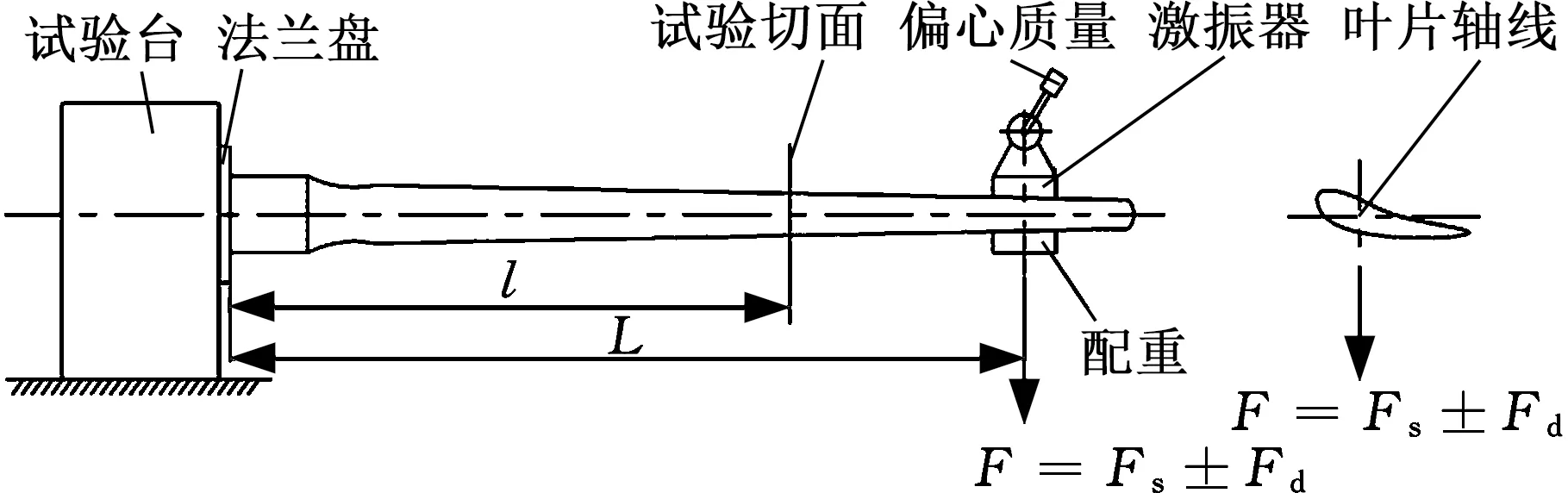
图2　疲劳试验原理[2]Fig.2　The principle of fatigue test[2]

叶片疲劳试验通过共振方式加载，根据一般系统的幅频响应曲线，当激振频率接近结构的固有频率时，振幅放大系数会变得很大，振幅放大系数的公式如下[3]：

(1)

式中，λ为激振频率与结构固有频率之比；β为振幅放大系数；ζ为阻尼比。

共振(λ=1)时，当阻尼比为1%，振幅放大系数为50；当阻尼比为2%，振幅放大系数为25。由此即可实现用小的激振力施加大载荷的目的。在实际试验中，叶片及试验系统的阻尼是固定的，因此放大系数依靠频率比λ来调节，在实际试验中，依靠调节电机转速来调节激振频率，从而达到调节激振载荷的作用。

3　叶片疲劳试验加载设计

叶片工作时的载荷主要来源于叶片承受的气动载荷，以及重力载荷等，这里统称为设计载荷。疲劳试验的目的就是模拟叶片承受的设计载荷来验证叶片的疲劳性能。

疲劳试验采用共振加载，沿展向的载荷分布取决于结构本身，而设计载荷沿展向的分布规律主要取决于叶片的气动特性，这两种分布很明显是不一致的，因此叶片试验标准[4-5]仅要求验证最危险截面的疲劳性能。但是随着叶片越来越长，叶片设计者和使用者都希望对叶片更多的截面进行疲劳试验验证，以确保叶片的使用性能。

典型的叶片各截面在寿命期内的损伤如图3所示，可见叶片损伤集中在某一区段，因此，以最大损伤截面为设计目标，兼顾考虑损伤较大的区段是可行的，而实现这个目标的重要一步就是计算出试验加载产生的各截面的弯矩载荷分布。这里给出两种计算加载弯矩分布比例关系的方法，并通过试验标定步骤来确定加载弯矩分布，验证两种方法的优劣。

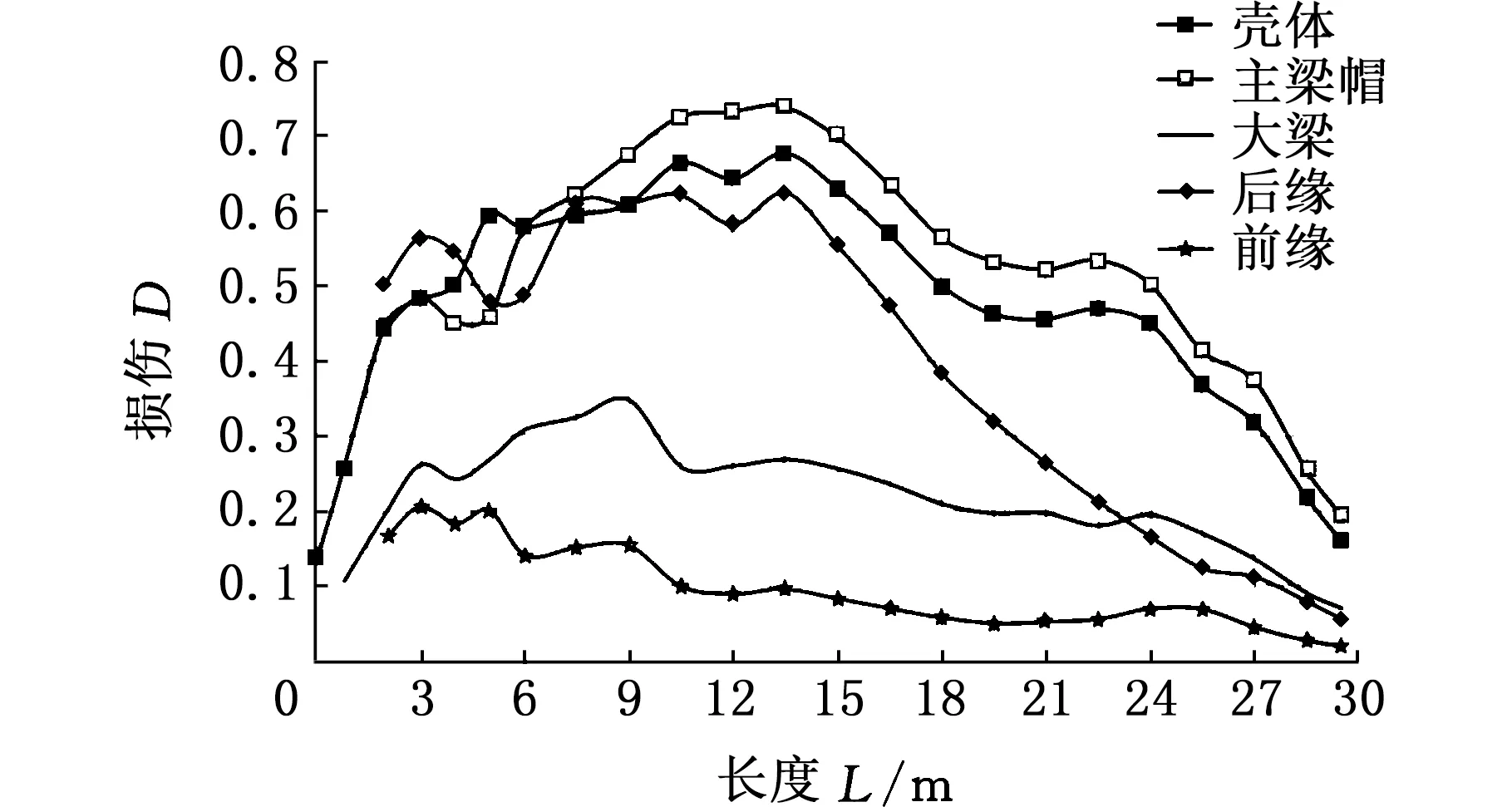
图3　叶片各截面损伤Fig.3　Blade section damages

3.1　惯性力公式计算截面弯矩分布

由于是共振加载，共振时叶片的载荷主要来源于惯性力而不是外界激励，故将叶片离散成多个微段，得到叶片上某个微段受到的惯性力，计算公式如下：

Fi=miai

(2)

式中,mi为微段的质量，{mi}即为叶片的质量分布；ai为微段的运动加速度。

根据前文所述，可以将叶片看作悬臂梁，振动时各微段可以看作正弦运动，微段的位移可表示为

Si=yisinωt

(3)

式中,yi为微段的振幅。

叶片可看作悬臂梁，{yi}为梁的挠度分布，ω为微段的振动圆频率，各微段的振动圆频率是一致的。

对位移求两次导数可以得到加速度

ai=-yiω2sinωt

(4)

因此微段的作用力改写为

Fi=-miyiω2sinωt

(5)

由上文可知，叶片疲劳试验激励是利用共振，那么叶片上各段之间的振幅比例应满足该阶频率下的振型，即

yi=Cφi

(6)

式中，C为常数；φi为位置i处的振型系数，{φi}为振型。

由此可得

Fi=-Cmiφiω2sinωt

(7)

假设叶片被离散成n个微段，每个微段到叶根的距离为xi，那么第m个微段上受到的弯矩可表述为

(8)

将Fi的表达式代入式(8)，得

(9)

叶片弯曲振动时，各微段振动周期相同且没有相位差，由此可得微段的最大弯矩值

(10)

根据前文所述，叶片设计时，质量分布和刚度分布是已知的，通过质量分布和刚度分布，可以采用振动力学的分析方法求得振型，因此质量分布{mi}以及振型{φi}是已知的，这样就可以得到叶片的加载弯矩分布比例关系。

3.2　挠度公式计算截面弯矩分布

根据材料力学公式中挠度与截面弯矩的关系，有

(11)

式中，EI为截面刚度；y为挠度；M为弯矩。

与第一种方法类似，考虑叶片被离散为n段，则微段m上的弯矩表示为

(12)

将挠度用振型系数表示，得到

(13)

式中，C为常数。

也就是说，通过数值方法对振型求二阶微分，然后与刚度分布的乘积即为叶片的加载弯矩分布比例关系。

大明路的整治的主要目标包括：“路平”、“优化交通功能”、“杆线地下工程”、“绿化景观改造”和“海绵城市建设”等。

3.3　弯矩分布计算方法的验证

前文提到，疲劳试验首先要考核损伤最大截面，那么就必须保证损伤最大截面上的试验弯矩，但是共振加载时截面弯矩很难直观求解出来，例如上面提到的两个方法中，都有一些常数不能给出数值；同时，试验中也需要监测最大损伤截面的弯矩载荷，以保证加载载荷的大小。考虑到玻璃钢材料在破坏前，应力应变基本成线性规律，可以采用应变来监测载荷。

试验时，根据损伤分析结果选择损伤最大位置，确定该截面位置的疲劳设计载荷，在叶尖某位置施加拉力，使损伤最大截面的弯矩达到设计弯矩，记录此时损伤最大截面的应变(对于挥舞方向，记录梁帽位置应变；对于摆振方向，记录前后缘位置)，此应变值称为标定应变，而这个过程称为叶片疲劳试验的静态标定过程。试验时监控应变达到标定值时，就表明损伤最大截面的加载载荷达到设计值。

通过标定过程，确定了一个截面的加载载荷，通过3.1节或3.2节可以确定加载载荷的分布关系，如此可以得到加载载荷分布。

以某59 m叶片参数为例，考虑激振器的重量，根据上文提到的两种方法分别计算共振加载下叶片各截面的弯矩分布，得到图4所示的弯矩分布曲线。由图4明显可以看出，两个方法得出的弯矩分布是一致的，只是由于第二种方法需要使用两次数值积分，因此结果产生了数值振荡。由此看来，利用第一种方法来计算弯矩分布更准确。

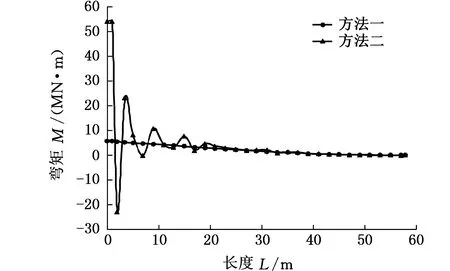
图4　两种方法计算的加载弯矩分布Fig.4　Loading moment distributions of two methods

3.4　试验考核区域的确定

得到试验加载弯矩分布后，将试验加载弯矩分布与设计弯矩分布比对，如图5所示，作用如下：一是可以保证叶片各截面不会超载，预防不必要的损伤；二是可以确定试验考核区域。如前文所述，叶片疲劳试验除了考核损伤最大截面的疲劳性能外，还希望考核损伤较大区段的疲劳性能，通过图5就可以直观地确定考核区域范围，如果考核区域不理想，就需要调节，根据3.2节的分析，可以在叶片展向布置局部质量或调整加载位置，调节质量分布和振型，从而改变疲劳加载载荷分布，将考核区域调节到使叶片损伤最大区段。

图5　设计弯矩分布与试验弯矩分布对比Fig.5　Comparison of designing and experimental moment distribution

4　叶片各截面刚度的获得

一般在叶片设计时，会给出设计截面刚度EI，但是由于叶片截面形状和铺层结构的复杂性，以及制造过程中的人为误差，实际制造出来的叶片截面刚度往往和设计值有较大误差，如果直接用设计截面刚度来设计疲劳试验，会导致疲劳试验载荷不准确，如果载荷偏小，起不到考察叶片的作用，如果载荷偏大，可能会过早破坏叶片。这里介绍一种简单的试验方法，以获得叶片各截面刚度EI的准确值。

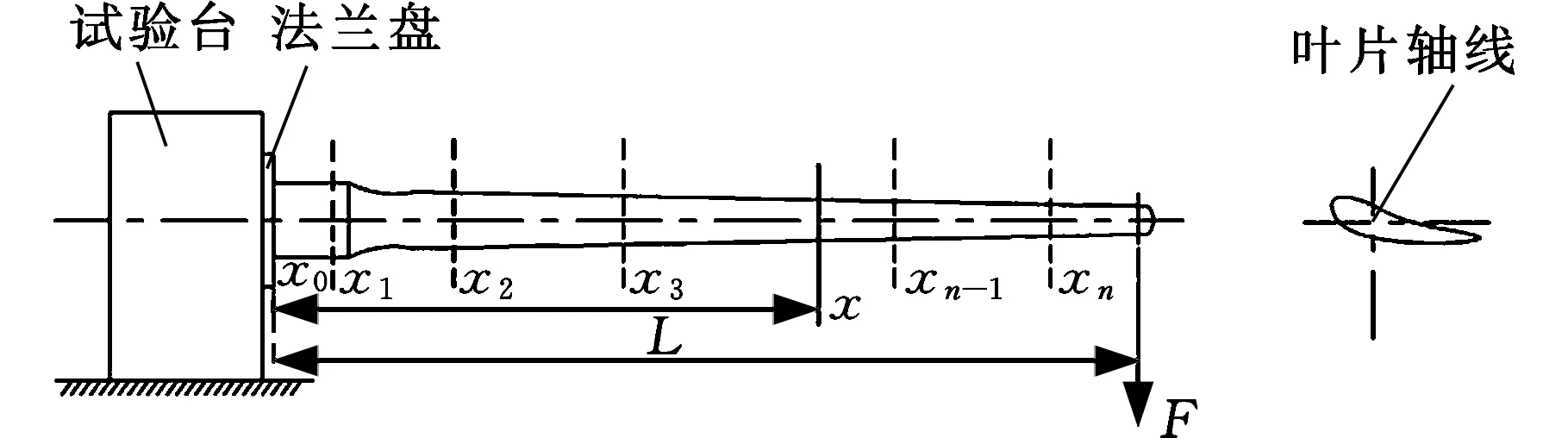
图6　叶片截面刚度测试原理Fig.6　The principle of blade cross-section stiffness test

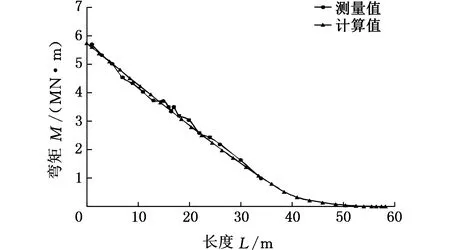
假设在叶尖部位施加集中载荷P，加载点距离叶根距离L，第i段上的点x(xi-1

M(x)=-P(L-x)

(14)

第i段的刚度可认为是常数，根据材料力学公式中挠度与截面弯矩的关系即式(11)，可得

(15)

i=1,2,…，n

在叶根固定约束端，有x0=0;y(x0)=0。

由此得到截面刚度：

(16)

i=1,2,…，n

根据叶片上的载荷P和n个截面位置的坐标x1,x2,…，xn，以及这些截面上的挠度测量值y(x1)，y(x2),…,y(xn)，确定叶片这些截面上的弯曲刚度EI(x1)，EI(x2),…，EI(xn)。

具体的测量步骤总结如下：①将叶片固定到试验台上；②确定叶片弹性轴位置；③测定叶根至集中载荷P加载点的距离L以及至各待测截面的距离x1,x2,…,xn；④在叶尖施加集中载荷P并记录数值大小，加载时注意P需通过截面弹性中心，对于准备进行疲劳试验的叶片，可以用激振器当作集中载荷；⑤测出各待测截面的挠度值y(x1),y(x2),…,y(xn)；⑥根据式(16)计算截面弯曲刚度EI(x1),EI(x2),…,EI(xn)。

需要注意的是，在进行以上公式推导时，没有考虑重力的影响，在已知叶片的质量分布的情况下，将叶片重力产生的弯矩代入公式中即可。该试验完全可以通过疲劳试验中的静态标定来实现，不需要额外开展试验。

5　疲劳试验设计实例

某型2MW叶片，经损伤分析得到疲劳考核截面为距叶根14.5 m处，首先通过静力试验测得各截面刚度分布，然后通过惯性力公式及考核截面设计弯矩计算加载弯矩分布，确定和调整考核区域。试验经静态标定后进行共振加载，如图7所示。

图7　共振加载Fig.7　Resonance loading

试验时，在叶片多个截面处布置应变片，根据截面的刚度、形状、尺寸以及应变片的位置推算截面弯矩，得到的加载弯矩测量值与计算值的比较如图8所示，试验设计方法得到验证。

图8　加载弯矩测量值与计算值比较Fig.8　Comparison between measured values and calculated values of loading moment

6　结语

本文从验证最危险截面的疲劳性能兼顾验证损伤较大区段的叶片疲劳试验要求出发，分析了叶片疲劳试验设计难点，推导出共振法叶片疲劳试验的加载弯矩分布计算方法，达到了疲劳试验的要求；给出了基于疲劳试验加载模式的附加试验方法，通过测试的方式获得叶片疲劳试验设计的基本参数，提高了叶片试验设计的准确性；文中提出的方法在随后的疲劳试验中得到验证。研究结论为进一步细化和优化叶片疲劳试验设计方案、完善叶片疲劳试验方法的理论体系提供了依据和参考。

参考文献：

[1]Composite Materials for Wind Turbine Blades. [EB/OL]. Qingdao:Gurit[2017-03-10]. http://www.gurit.cn/composite-materials-for-wind-turbine-blades.aspx.

[2]傅程. 风轮叶片疲劳损伤演化及气动弹性研究[D]. 北京：北京航空航天大学, 2009.

FU Cheng. Research on Fatigue Damage Evolution and Aeroelastic Simulation of Wind Turbine Blades[D]. Beijing：Beihang University, 2009.

[3]倪振华. 振动力学[M]. 西安：西安交通大学出版社, 1986：79-92.

NI Zhenhua. Vibration Mechanics[M]. Xi’an：Xi’an Jiao Tong University Press, 1986:79-92.

[4]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB/T 25383-2010. 风力发电机组风轮叶片[S]. 北京：中国标准出版社，2010.

General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China, Standardization Administration of the People’s Republic of China. GB/T 25383-2010. Wind Turbine Generator System—Rotor Blades[S]. Beijing：China Standard Press，2010.

[5]IEC. IEC 61400-23, Wind Turbine Generator Systems—Part 23:Full-scale Structural Testing of Rotor Blades[S]. Geneva: IEC, 2001.

[6]陈文俊. 弹翼剖面弯曲刚度的确定方法[J]. 系统工程与电子技术, 1996(8):77-81.

CHEN Wenjun. Method for Determining Bending Stiffness of Elastic Wing Section[J]. Systems Engineering and Electronics, 1996(8):77-81.

(编辑王旻玥)