六自由度主被动一体隔振平台的动力学实验建模

郝慧荣，白鸿柏，张慧杰，李冬伟，刘树峰

（1.军械工程学院，石家庄 050003；2.内蒙古工业大学，呼和浩特 010051）

精密的电子、光学设备为避免来自空间的冲击与振动的影响与损坏，通常需要采用隔振平台来进行防护，六自由度隔振就是在这样的背景下产生的一种防护技术；主被动一体隔振平台是在传统的被动隔振基础上添加主动控制力，其可以克服传统被动隔振在低于固有频率时无法隔振的弱点［1～5］。

要实现六自由度平台的主被动一体隔振就必须建立起其动力学模型，这是实现隔振的主动控制的前提，也是能否达到满意控制效果的关键。

实验建模又叫做实验模态参数辨识，是系统辨识的一个方面。模态参数辨识的方法很多，有时域辨识方法，也有频域辨识方法。这里采用的是时域辨识，即对结构上某一点激励，同时测得激励点与响应点的时域信号，根据多自由度振动的理论知识，利用最小二乘递推算法辨识出模态参数［6－7］。

文献［8］虽然曾对主被动一体隔振平台进行过实验建模，但其存在以下几点不足：① 利用锤击脉冲激励信噪差，得到频响函数准确性不高；② 所辨识的模型只是基于平台本身考虑而不包含作动器，因此，得到的模型只是整个控制系统的子系统，还得单独建立作动器的动力学模型。文献［9］实验建模采用平台自身作动器快速正弦扫描激励虽然提高了信噪比，但其因作动器分组而带入一些计算增加了模型的不确定性。

1 六自由度主被动一体隔振平台测试系统

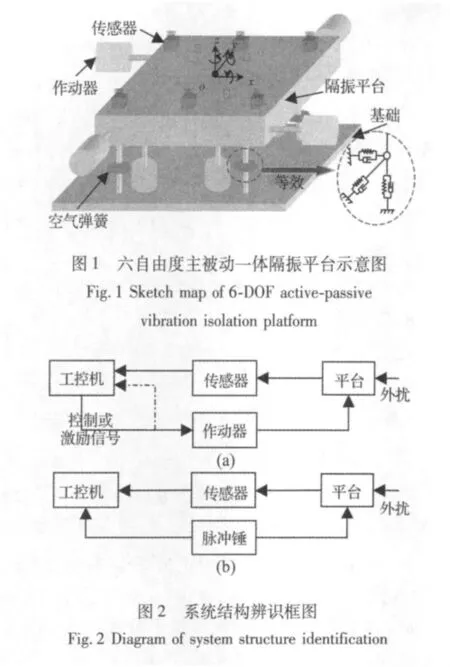
六自由度主被动一体隔振平台如图1所示，其由4个空气弹簧被动支撑，每个空气弹簧可等效为具有三向刚度、阻尼的六自由度铰［10］；6个传感器监测隔振平台的振动情况，将信号反馈给控制器；8个作动器将根据控制器的指令为平台提供主动控制力，且作动器的安装不影响平台的六个自由度。图1中6个传感器中的1、3、5 为垂直传感器，方向同z正向；2、4、6 为水平传感器，2的方向同x正向，4的方向同y正向，6的方向同y反向；8个作动器中的1、2、3、4水平放置，5、6、7、8垂直放置。1方向同y正向；2方向同x反向；3方向同y反向；4方向同x正向；5、6、7、8方向同z正向。

要对平台进行主动控制，前提条件是需要知道控制对象的动力学模型，整个主被动隔振系统的模型结构辨识如框图2（a）所示，这里需要说明的是：在进行隔振主动控制时没有图2（a）中的虚线，而在实验建模系统辨识时需用到虚线连接，主动控制时工控机作为控制器向作动器发出控制信号，而在系统辨识时工控机作为信号发生器向作动器发出激励信号；作为对比，图2（b）给出了文献［8］中提到的辨识方法框图，从中可以发现：图2（b）所辨识结果是图2（a）的一部分只是平台本身。

2 惯性参考坐标到传感器坐标的变换

在考虑空间六自由度隔振问题时就会涉及到转动，而转动会带来方向余弦矩阵R，即旋转运动时的坐标变换，一般采用多刚体的旋转坐标法，最普遍采用欧拉角坐标，记 α、β、γ 为欧拉角，则：

式中c表示cos（·），s表示sin（·）。当平台只发生微小转动时，有 cos（·）≈1，sin（·）≈（·），sin（·）sin（·）≈0坐标系的旋转矩阵R可以简化为：

式（2）的简化使得六自由度动力学方程变为了线性方程，这时可认为欧拉角就是绕各惯性坐标轴的转角。在物理空间，选取坐标原点建立坐标系后（参见图1），隔振平台上任意点b与隔振平台质心o的位移的关系可表示为：

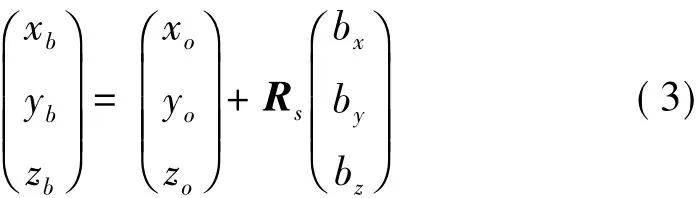
其中xb、yb、zb为b点的三个方向上的坐标；xo、yo、zo为平台质心o的惯性位移坐标；bx、by、bz为b点在平台质心为坐标原点的“固连坐标系”下的坐标。由式（3）有下面的式子成立：

其中q=（q1q2…q6）T为6个传感器监测的信号；zb1、xb2…yb6为6个传感器在惯性坐标下沿着其测试方向的位移；x=（xo，yo，zo，α，β，γ）T为六自由度的物理坐标；bx1、bx2…bx6，by1、by2…by6，bz1、bz2…bz6为 6 个传感器在平台“固连坐标系”下的坐标。φ是传感器的布置矩阵，若det（φ）≠0则有下式成立：

由式（4）可知，若能完整监测六个自由的运动情况，传感器布置必须满足det（φ）≠0的条件。

在物理坐标下六自由度的动力学方程为：

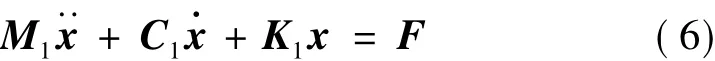
其中M1、C1和K1分别为在惯性参考坐标系下的质量、阻尼和刚度矩阵；F=（fx，fy，fz，Mx，My，Mz）T是物理坐标下沿着三个方向的力与绕三个方向的力矩。在满足det（φ）≠0的情况下，式（6）可变为：

或写为：

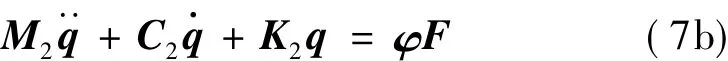
其中：M2=φM1φ－1、C2= φC1φ－1和 K2= φK1φ－1分别为在传感器坐标系下的质量、阻尼和刚度矩阵。

设dx1…、dy1…、dz1…为8个电磁作动器在平台“固连坐标系”下的坐标，则有下面的式子成立：

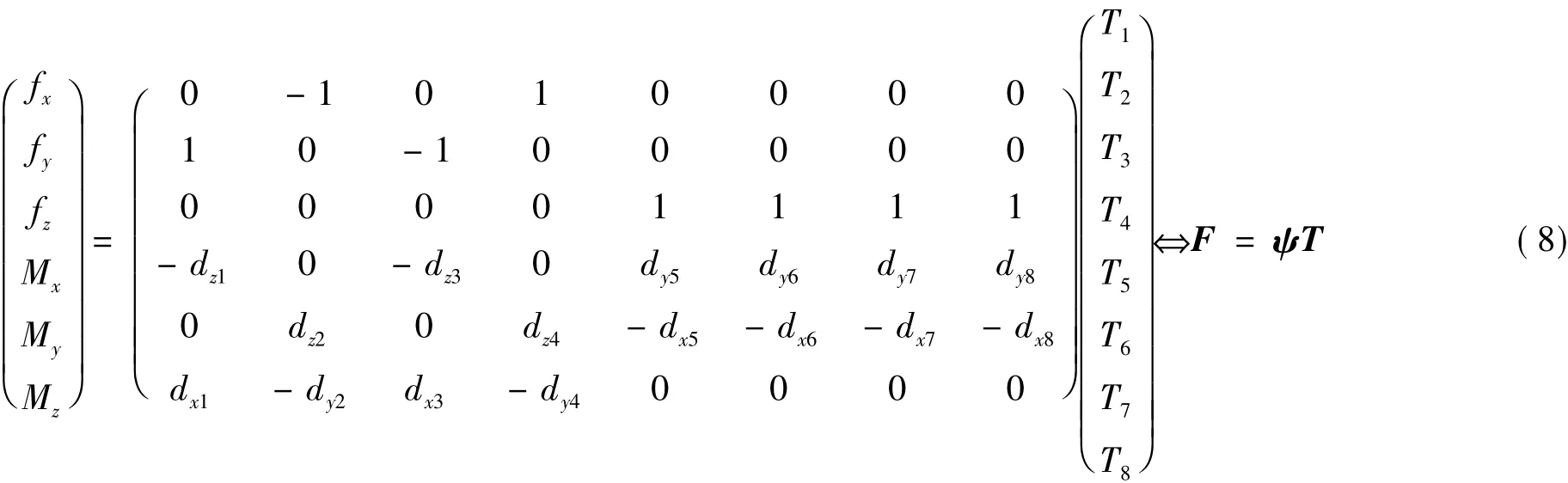
其中T=（T1T2…T8）T是作动器的输入激励力，ψ是作动器的布置矩阵。

若传感器与作动器都是线性的则有：

其中Λq、ΛT是6个传感器与8个作动器的物理量与电压向量Uq、UT的标定系数矩阵，将式（8），式（9）带入式（7）得：

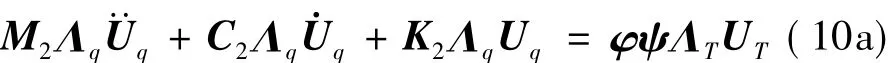
或写为：

其中：

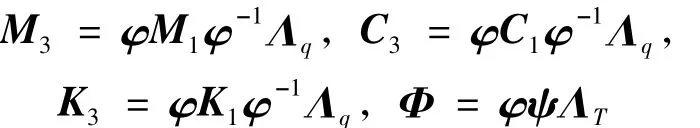
由det（φ）≠0可推出det（M2）≠0，式（10b）可化为：

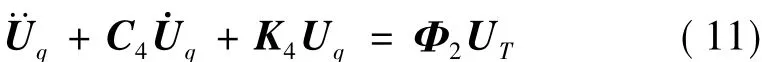
其中，C4=M－13C3，K4=M－13K3，Φ2=M－13Φ1，质量阵化为了单位矩阵。

化为式（11）的好处是可以不必再关心传感器布置矩阵φ与作动器布置矩阵ψ的具体数值，也不必再关心它们的标定系数矩阵Λq、ΛT的具体数值，直接建立起输入与输出之间的动力学模型，可以最大限度的减少模型的不确定性，实现整体建模。再有化为（11）式为参数估计提供了一个简洁的模型。

3 最小二乘估计递推算法

通过观察式（11）可以发现：式（11）的每一行有20个待辨识的参数，整个方程组总共有120个参数。在实际的辨识实验中，可以直接通过观测得到电压向量Uq、UT，而将Uq信号数值微分一次、两次就可以知道、。不能直接使用式（11）进行参数辨识，需将其化为参数估计模型。将式（11）的第i行（i=1，2…6）展开变化为：

Yi（j）是j×1的观测矢量，H（j）是j×20的观测矩阵。在最小二乘准则下：

记 P（j）=［H（j）T·H（j）］－1为信息矩阵，增加一次新的观测：

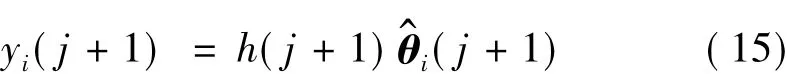
由矩阵反演公式［7］知：

其中K（j）为增益矩阵：

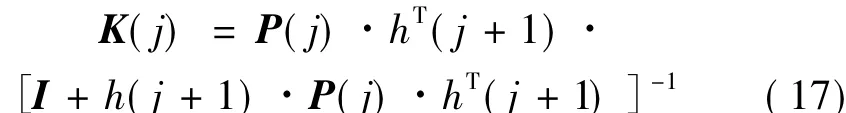
进一步推得待估参数矢量的递推公式为：

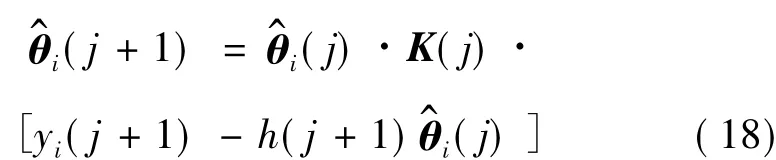
4 辨识结果

参数进行辨识实验的具体做法是：利用主被动一体隔振平台的8个电磁作动器分别对平台进行力扫频激励，通过6个传感器测得平台的位移响应信号，将激励与响应信号都记录下来后，带入辨识的状态方程进行参数辨识（或叫做参数估计）。

平台实验建模的测试设备为：传感器采用的是中国地震局制造的941B型低频测振仪；A/D转换采用的是PCI－1713多通道12位采集卡；D/A转换采用的PCI－1723多通道16位输出卡；作为平台振动激励的作动器与功放采用的是课题组开发研制的音圈电机以及其功放，整个系统实物如图3所示。快速正弦扫描在整个测试频段内能获得平谱，且激励能量相同，信噪比大，精度高，因此这里激励信号选用快速正弦扫描。

图3 六自由度主被动一体隔振平台实物图Fig.3 6-DOF active-passive vibration isolation platform

当用振动控制仪给每个作动器分别施加频率3 Hz～30 Hz，振幅1 V如图4所示的扫频激励信号时，六个传感器实测到的位移电压信号如图5所示。通过前文实验建模中的辨识方法，可得到六自由度隔振平台的标称参数矩阵为：

图4 八个作动器扫频激励信号Fig.4 The frequency sweep signal of the eight actuators

图6给出了应用最小二乘递推算法，当i=1时的误差曲线，可见参数的估计值是趋于稳定的，当i=2，3…6时有类似的误差曲线。

知道了C4、K4和Φ2后就可以方便的写出未加控制时的系统状态方程：

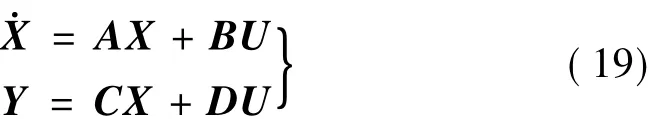
图5 八个作动器分别扫频激励六个传感器测的位移信号Fig.5 Displacement signals of the six sensors under the eight actuators separately frequency sweep actuation

式（19）中系统状态方程阶次是12阶，有了未加控制时的系统状态方程，就可以进行下一步的振动主动控制器的设计了，这里不再赘述。

图6 误差曲线Fig.6 The curve of error

5 结论

本文与文献［8，9］的模型辨识最大的不同是在时域进行而非频域，在频域辨识每次只能使用一个传感器的信息，信息掌握不全面，而且每个单独辨识容易造成虚假（噪声）模态的产生，最终整个系统的阶次会很高，使用时域的方法六个传感器的信息都被使用，最终的系统状态方程阶次只有12阶。另外，通过模型参数的辨识发现如下几点结论：

（1）利用作动器作为激励源信噪比高，可以直接辨识出整个系统的模型，比分模块辨识减少了工作量；

（2）空间物理坐标到传感器坐标的变换，既使得不必再关心传感器与作动器的位置矩阵具体的数值，也不必再关心它们的标定系数矩阵的具体数值，可以方便的建立起输入与输出之间的动力学模型；

（3）若要能完整监测六个自由的运动情况，传感器布置矩阵φ必须满足det（φ）≠0的条件；

（4）最小二乘估计递推算法较普通最小二乘估计和迭代最小二乘估计工作量最小。

利用实验建模给出的状态方程为下一步的隔振平台的振动主动控制打下了基础。

［1］罗煜峰.基于Matlab的六自由度隔振系统计算［J］.机械与电子，2007，（8）：73 －75.

［2］陈修祥，马履中.车载设备多维振动控制装置的设计及模态研究［J］.自然科学进展，2007，17（4）：551 －555.

［3］朱 伟，马履中，等.基于三平移并联机构的三维减振平台建模与仿真［J］.农业机械学报，2008，39（1）：142 －146.

［4］ Nakamura Y，et al.Development of active 6-DOF micro vibration control system using giant magnet astrictive actuator.Proceedings of the SPIE Conference on Smart Systems for Bridges Structures and Highways［C］.SPIE-International Society for Optical Engineering，1999，229－240.

［5］Thomson W T，Dahleh M D.Theory of vibration with applications（Fifth Edition）［M］.影印本.北京：清华大学出版社，2005.

［6］傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000.

［7］刘 君，夏智勋，编著.动力学系统辨识与建模［M］.长沙：国防科技大学大学出版社，2007.

［8］张春良.微制造平台振动主动控制研究［D］.杭州：浙江大学，2003.

［9］侯军芳.六自由度微动精密平台主动隔振技术研究［D］.石家庄：军械工程学院，2009.

［10］ C.M.哈里斯，C.E.克瑞德，主编.众师，译.冲击和振动手册［M］.北京：科学出版社，1990.