带滞变支撑悬臂输流管的动力响应分析

黄 茜，臧峰刚，张毅雄，叶献辉，蔡逢春

（核反应堆系统设计技术国家级重点实验室，成都 610041）

近年来，输流管内的轴向流引发的流致振动问题得到了广泛的关注［1］。人们针对输流管的非线性振动做了不少卓有成效的工作，就细长悬臂输流管而言，这些工作主要包括：逐步建立并完善了输流管的非线性运动微分方程［2，3］，研究了定常流与振荡流作用下输流管的稳定性分析［4－12］。

滞变支撑（Energy absorber）的恢复力是变形与速度的函数，在加卸载过程中不是沿着同一个路径变化，而是形成如图1所示的滞变曲线，这种特性能使滞变支撑在地震等紧急工况下大量耗能以保障结构安全。因此，这种支撑已被用于核工业，土木工程、建筑工程等领域。然而迄今为止，却鲜有带滞变支撑输流管流致振动的研究报道。

本文基于能量法，将滞变支撑所做的虚功引入到管道的能量方程中，结合悬臂管道的不可伸长假设，导出了带滞变支撑的悬臂输流管的非线性运动方程。随后，采用Matlab程序编制了数值计算程序，考察了该系统的动力学响应。

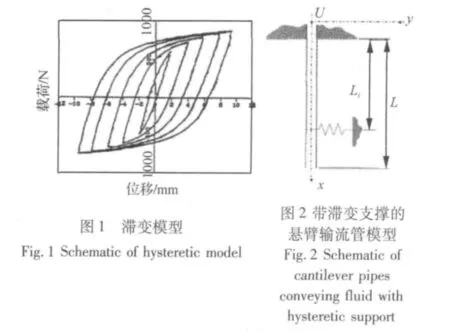
1 带滞变支撑悬臂输流管道的理论模型

悬臂管长为L，横截面积为A，单位长度管道的质量为m，抗弯刚度为EI，流体的轴向流速为U，单位长度流体的质量为M，x表示管道横截面位置，y表示管道轴线偏离平衡位置的位移，并引入沿管道轴线的曲线坐标s。假设在初始条件下管道沿x轴竖直放置，如图2所示。

悬臂输流管的基本假设为：① 流体不可压缩，管内流速保持不变；② 管径与管长之比很小，管道为欧拉梁；③ 不计管道的转动惯量和剪切变形；④ 管道运动为平面运动且中心轴线不可伸长；⑤ 管道可以是大变形但应变很小。

基于Hamilton原理，带滞变支撑的悬臂输流管系统的能量方程为：

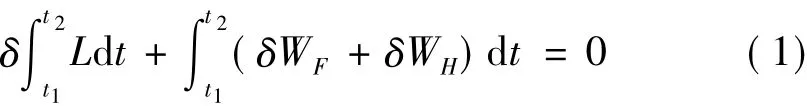
式中L=VP+VF－TP－TF，VP和VF是管道与流体的势能，TP和TF是管道和流体的动能。第二个括号表示非保守外力虚功，其中，δWF为流体力对系统做功，δWH为滞变支撑对系统做功。

2 滞变支撑对系统做功

若沿输流管轴线共布置了个P个滞变支撑，其中，第i个支撑距管道固定端的距离为Li，假设输流管与滞变支撑连接点轴向变形很小，滞变恢复力的轴向分量可忽略不计。借助BOUC-WEN光滑滞变模型［13］，当管道受到外部激励发生振动时，作用其上横向滞变力可表示为：

对第i个支撑而言，ki代表其初始刚度，αi为支撑屈服后刚度与屈服前刚度之比，yi为支撑点的横向变形，Zi称为滞变位移，A，Δ，Θ和n是控制滞变位移初始刚度、幅值和滞变形状的滞变特性参数。只需调整这些参数，BOUC－WEN模型便可用来表达各种软化、硬化滞变曲线，因此该模型又被称为“万能模型”。

本文仅考虑含1个滞变支撑的情形，即P=1，同时取滞变特性参数n=1。由虚位移原理可知，在t1～t2时间段内，滞变力Fh在虚位移δy上所做的虚功为：

3 带滞变支撑悬臂输流管动力学微分方程及其求解

假设管道材料的耗散为粘弹性耗散，满足Kelvin-Voigt模型，其应力－应变关系表示为：

其中，a为粘弹性阻尼系数，对平面问题而言，管道的横向位移与管长相比为一阶小量，即：y=v～O（ϑ），ϑ≪1，本文方程中的变量精确到4阶小量O（ϑ4）。

将式（3）与式（4）代入式（1）结合式（2），通过分部积分、合并同类项等数学变换，可得到受滞变支撑作用的悬臂输流管的非线性运动方程：

当α1=1时，方程（5a）第一行代表滞变恢复力的非线性项［α1k1y+（1－α1）k1Z］δ（s－L1）与滞变位移ZL1不再相关，简化为线性项k1yδ（s－L1），此时，模型退化为带线性弹簧支撑的非线性悬臂输流管。

为便于计算与分析，引入下列无量纲量：

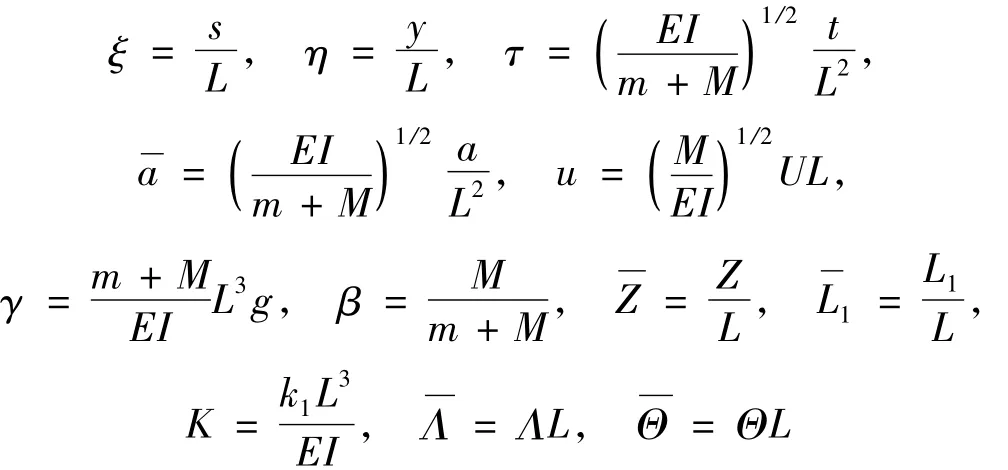
由于非线性运动方程为复杂的偏微分方程，不能直接求解，为此，作2阶模态的Galerkin展开式：

其中，qi为广义坐标，φi为输流管的振型函数，代入式（5）并无量纲化后有：

其中：

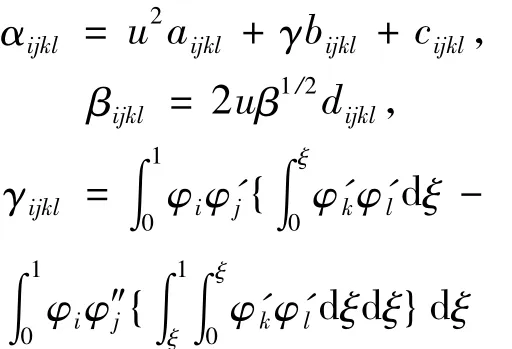
其余非线性项bij，cij，dij，aijkl，bijkl，cijkl及dijkl的详细表达可参考文献［14］。

4 算例分析

4.1 计算参数

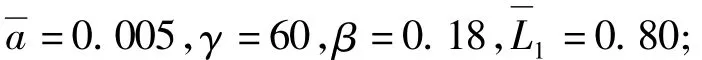
4.2 退化的带滞变支撑悬臂输流管模型

根据第3节推论，通过调整参数α1的取值，滞变支撑模型退化为线性支撑模型。为了证实该结论，本文画出了带滞变支撑（α1=1，K=100）的悬臂输流管分叉图，并与文献［14］带线性支撑悬臂输流管（K=100）的结果进行了比较。分叉图的横坐标为输流管内流速，纵坐标为悬臂管末端的稳态位移响应幅值，由此可观察系统在不同流速取值点的运动状态。为保证分叉图的完整性，本文分别选取正、负位移作为初始条件（条件1∶q1（0）= －0.001；条件2∶q1（0）= －0.001，其余初始条件为零）进行数值计算，其结果呈现在图3中。

本文计算结果表明，带滞变支撑悬臂输流管首次失稳为静态失稳，失稳临界流速为u=11.49；随着流速增加，当u=12.42时，结构发生动态颤振失稳（文献［14］静态失稳为u=11.47，动态颤振失稳为u=12.43），结果几乎完全一致，微小差别是数值计算引起的。同时，由图3可知在8≤u≤22的整个流速范围内，悬臂管末端的稳态响应幅值随流速增加呈逐步增长趋势两结果也几乎完全重合。由此验证了本文模型的合理性与正确性。

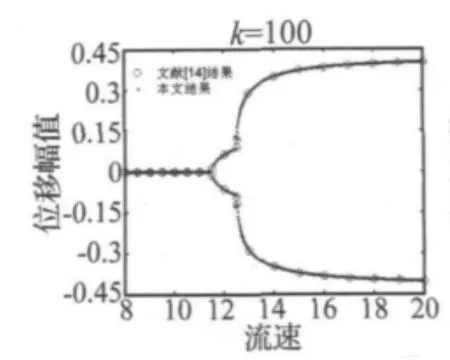
图3 退化模型合理化验证Fig.3 Validation of the degenerate model

图4 流速参数区域分叉图Fig.4 Bifurcation diagram with fluid velocity

4.3 带滞变支撑悬臂输流管的响应分析

带滞变支撑的悬臂输流管存在极其复杂的动力学行为，图4为K=200模型的分叉图，从该图可以看出：具有滞变特性支撑的悬臂输流管存在极其复杂的动力学行为，图4为K=200时系统的分叉图，从该图可以看出，随着流速的增大，系统将由稳定变为不稳定，可能发生屈曲、周期、混沌等复杂响应。其中，u=9.5是系统的Pitchfork分岔点，当流速u＜9.5时，系统的能量耗散大于流体非保守力做功，平衡点为稳定的焦点，任何扰动经过一段时间后将回到平衡点；当9.7≤u≤14.5，系统发生屈曲失稳；管道相图如图5（a）所示；u=14.6是系统由静态屈曲运动过渡到动态极限环运动的分界点，系统发生周期7的极限环振动，如图5（b）所示；当流速略增长，位于u∈［14.7，14.9）的区间时，系统运动变为对称的周期5极限环运动，如图5（c）所示；此后，当14.9≤u＜15.4时，系统发生叉式分岔，两种初始条件可得到两种非对称的周期5极限环，图5（d）与图5（e）分别为u=15时两种不同初始条件下系统的相图，此时的功率谱图为图5（f），不难看出，该流速的功率谱为离散的谱线，可以清晰的辨别出系统的振动频率；同样是u=15时刻，图5（g）与图5（h）为滞变支撑与管道交汇点对应的相图与功率谱图，通过与图5（d）－图5（f）的结果对比可发现，同一流速下输流管各个部位的振动形式有显著差异，但其振动频率却是相同的。在15.5≤u≤17.1的区间范围内，系统振动将主要表现为混沌运动［图6（a），6（c）］，其间夹杂着周期振动［图6（b）6（d）］；由响应分叉图可以观察到，系统的振动幅值与主频在流速点u=17.2处有明显的跳跃，这种跳跃对应着系统振动性态的突然改变；此后，随着流速的增大，管道的振动将维持周期1运动［图6（d）］，而响应的振幅也将随流速增加而逐渐增大。

4.4 滞变支撑刚度对悬臂输流管稳定性的影响

支撑的刚度能刻画运动约束的软硬程度，这种软硬程度将会引起系统的动力学行为发生改变。K=100，K=150，K=200，K=250 与K=300 对应的系统响应分叉图分别如图7（a），图7（b），图4，图7（c）及图7（d）所示。

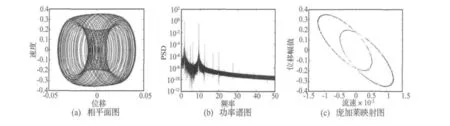
图8 系统的概周期运动（K=100；u=12.5）Fig.8 The quasiperiodic oscillation for the system with K=100；u=12.5

带滞变支撑悬臂输流管除了发生屈曲、周期、混沌运动外，还可能发生概周期运动：若K=100，且流速为12.3≤u≤12.6时，系统的相平面图显示为紊乱且不重合的轨迹［图8（a）］，这种轨迹只可能存在于混沌或概周期运动中，为了鉴别系统真实的运动状态，需要作出此时系统的功率谱与庞加莱映射图：功率谱图［图8（b）］表明该响应具有显著的周期运动特性，而其庞加莱映射［图8（c）］呈现为两个封闭的椭圆图案，仿真结果表明，系统响应为概周期运动。

通过对分叉图的比较可以发现，当K≥100时，随着无量纲化支撑刚度K的增加，系统发生首次失稳的临界流速值会逐渐降低，而发生大幅跳跃的流速值会逐渐增加。此外，系统出现复杂响应（多周期、概周期与混沌运动）的参数范围将逐渐减小，直至系统不再出现复杂响应。

总之，刚度的变化不仅使使得系统的分叉类型、分叉方式与分叉路径发生了的显著变化，并使其出现复杂响应的参数范围发生了改变，也改变了周期运动的周期数。因此，运动约束的软硬程度对系统的动力学响应有较大影响。

5 结论

利用Hamilton体系的变分原理，导出了带滞变支撑悬臂输流管的非线性运动方程，通过数值模拟与算例分析，可得以下几点结论：

通过滞变支撑退化模型与现有文献结果比较，证实了本文模型的合理性与有效性。

滞变支撑悬臂输流管表现出丰富的动力学行为，随着流速的增大，系统将由稳定变为不稳定，系统的运动形式可能为屈曲失稳、周期、概周期，混沌运动等。

支撑刚度是决定系统稳定性的重要因素之一。随着支撑刚度的增加，系统发生首次失稳的临界流速值会逐渐降低，发生跳跃的流速值反而会逐渐增加；此外，系统出现复杂响应的参数范围将逐渐减小。

［1］任建亭，姜节胜.输流管道系统振动研究进展［J］.力学进展，2003，33（3）：313－324.

［2］ Lee S I，Chung J.New non-linear modeling for vibration analysis of a straight pipe conveyingfluid［J］.Journal of Sound and Vibration，2002，254（2）：313－325.

［3］ Semler C，Li G X，Paidoussis M P.The nonlinear equations of motion of pipes conveying fluid［J］.Journal of Sound and Vibration，1994，169（5）：577－599.

［4］Wadham-Gagnon M，Paidoussis MP，Semler C.Dynamics of cantilevered pipes conveying fluid.Part1： Nonlinear equations of three-dimensional motion［J］.Journal of Fluids and Structures，2007，23：545－567.

［5］Paidoussis M P，Semler C，Wadham-Gagnon M.Dynamics of cantilevered pipes conveying fluid.Part 2：dynamics of the system with intermediate spring support［J］.Journal of Fluids and Structures，2007，23：569 －587.

［6］ Modarres-Sadeghi Y，Semler C.Dynamics of cantilevered pipes conveying fluid.Part 3：Three-dimensional dynamics in the presence of an end-mass［J］.Journal of Fluids and Structures 2007，23：589－603.

［7］Jin J D，Song Z Y.Parametric resonances of supported pipes conveying pulsating fluid［J］. JournalofFluidsand Structures，2005，20 763 －783.

［8］Wang L.A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid［J］.Journal of Non-Linear Mechanics 2009，44：115－121.

［9］包日东，闻邦椿.分析弹性支承输流管道的失稳临界流速［J］.力学与实践，2007，29（4）.24 －28.

［10］包日东，金志浩，闻邦椿.一般支承条件下输流管道的非线性动力学特性研究［J］.振动与冲击，2009，28（7）：153－157，186.

［11］金基铎，杨晓东，邹光胜.两端支承输流管道的稳定性和临界流速分析［J］，机械工程学报，2006，42（11）：131 －13.

［12］金基铎，杨晓东，张宇飞.固定约束松动对输流管道稳定性和临界流速的影响［J］.振动与冲击，2009，28（6）：95－99.

［13］欧进萍，王光远.结构随机振动［M］.北京：高等教育出版社，1998.

［14］ Paidoussis M P.Fluid-structure interactions［M］.London：ACADEMIC PRESS，1998.