基于工作应变模态损伤识别方法的试验研究

顾培英，邓 昌，汤 雷

（1.南京水利科学研究院，南京 210029；2.水利部水科学与水工程重点实验室，南京 210029）

结构损伤诊断首先需解决损伤标识量的选择问题，李德葆等［1］研究得到了六种损伤识别指标的灵敏度，应变型指标比位移型指标对损伤具有更好的识别能力。笔者也进行了相关试验研究和数值仿真分析，得出简支梁和渡槽结构应变模态损伤规律及其损伤识别优势［2～5］。但目前所涉及的损伤指标法大多数是基于位移类模态（或参数）。

损伤状态下的模态数据需通过模态试验获得，而传统的模态试验需对结构进行人工激励，但此方法无法实现在线试验，且许多结构人工激励又较为困难，所以，人们提出了基于环境激励的位移模态试验方法。该方法已在航天、航空、汽车、建筑及桥梁领域成功应用，但本文讨论的是基于环境激励的应变模态问题。这里定义环境激励下的应变模态为工作应变模态OSMS（Operational strain mode shape）。目前，笔者已建立了基于环境激励下的工作应变模态识别法［6，7］，并开展了应变模态数值仿真分析［3］、人工激励下的应变模态模型试验［2，4］。

现有损伤指标法是结合有限元模型分析，根据实测模态数据，利用结构损伤前后动态参数变化构造合适的损伤指标，判别损伤的存在、位置或程度。常用的损伤识别指标主要有两类［8～10］：①相关弱化型，以损伤前后相关系数弱化为损伤识别指标；②极差型，以损伤前后模态参数差为损伤识别指标。但在实际结构损伤评估中，要得到损伤前的精确状态非常困难。为此，笔者近几年提出了基于损伤应变模态差分（Strain Mode Shape Difference）原理的损伤位置直接指标法ISMSD、基于局域应变模态面积（Local Strain Mode Shape Area）的损伤程度直接指标法ILSMSA，两指标无需利用损伤前的模态数据［8，11］。

本文在简要介绍以上方法的基础上，针对环境激励下的应变模态进行模型试验研究，验证所提出的工作应变模态识别方法；并结合数值仿真分析，验证并完善了所提出的损伤识别方法。

1 工作应变模态频域识别方法

文献［6］中推导得到具有粘性阻尼n自由度系统的应变频响函数矩阵Hε（ω）为：

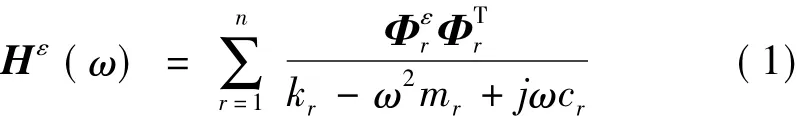
式中：Hε（ω）为应变频响函数矩阵；Φr为第r阶位移模态矢量；为第r阶应变模态矢量；kr、mr、cr分别为第r阶模态刚度、模态质量、模态粘性比例阻尼系数。

根据式（1）可知，应变频响函数矩阵任一列包含了应变模态的所有信息，因此环境激励位移模态试验频域法完全可应用到应变模态中来。

2 损伤识别直接指标法

2.1 损伤位置直接指标法

梁式结构研究结果表明，损伤影响区范围可近似地由损伤点为中心的三段直线组成［11］。j点损伤位置直接指标值可表示为［11］：

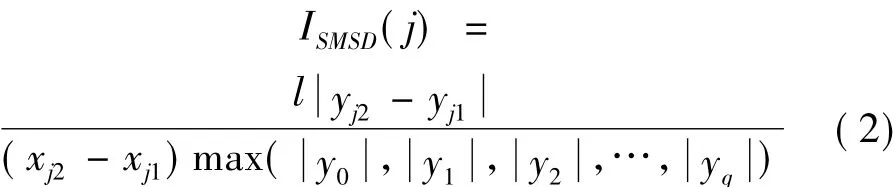
式中：ISMSD（j）为某阶应变模态差分曲线第j个有效零值点损伤位置直接指标值；l为梁式结构跨度；xj1、xj2为对应于有效零值点j的有效极值点x值；yj1、yj2为对应于有效零值点j的有效极值；y0、y1…yq为所有有效极值；q为有效极值点个数。

ISMSD（j）值越大，j点处损伤可能性越大。再结合差分曲线变化规律，即可判断损伤位置。

2.2 损伤程度直接指标法

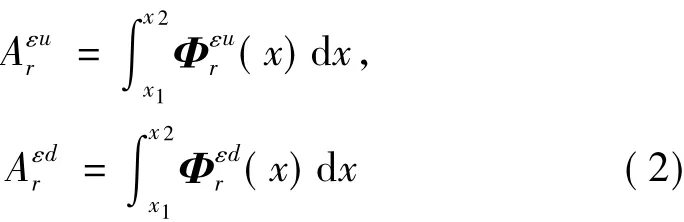
令r阶应变模态损伤面积为Δ，则：

式中：IrLSMSA为第r阶局域应变模态面积损伤程度直接指标。

3 模型试验

模型采用工字钢悬臂梁，图1为模型截面图。该模型梁长3.00 m，分别在距自由端2.60 m和2.90 m处采用螺栓固定。模型划分成30等份，共31个测点，在各测点（位于上腹板）粘贴电阻应变计。首先对完好悬臂梁进行锤击激励下的应变模态、环境激励下应变模态（即工作应变模态）试验，再分别在 1.80 m、1.00 m上翼缘处切割1 mm宽的裂缝，裂缝深度为整个翼缘厚度。共开展6组工况的应变模态试验。

图1 模型截面图（单位：mm）Fig.1 Section of model（unit：mm）

3.1 工作应变模态

通过第1节介绍的应变模态识别方法识别出前二阶工作应变模态，图2为工作应变模态与锤击激励下的应变模态比较，其中1损伤表示在1.80 m处存在损伤，2损伤表示分别在1.80 m、1.00 m处存在损伤。

根据图2可知，利用笔者提出的方法识别出的工作应变模态与锤击激励下的应变模态形状相似，除支座和节点附近外，各工况下的振型相对值平均相差6%。所以，该方法可较好地识别工作应变模态。此外，第1阶应变模态在1.80 m、1.00 m损伤处变化较为明显，第2阶应变模态在1.00 m损伤处变化较为明显。

3.2 损伤位置直接指标

图3为工作应变模态差分曲线，由图3可知，完好状态下的工作应变模态差分曲线除固定支座附近外，变化较为平缓。损伤状态下的工作应变模态差分曲线在损伤处发生剧烈变化，从极大（或极小）值经过损伤点很快达到另一极小（或极大）值。两极值点之间几乎呈直线关系，极值点外一定影响范围内的差分曲线也几乎呈直线，一定范围之外，该直线逐渐过渡到另一较为平坦的曲线或直线。两过渡点间的范围即为损伤影响区，简而言之，损伤影响区范围可近似地以损伤点为中心的三段直线组成，该结构平均损伤影响区范围为0.49m。对于多损伤结构，只要损伤间距大于影响区范围，损伤位置即可按单损伤方法判定。

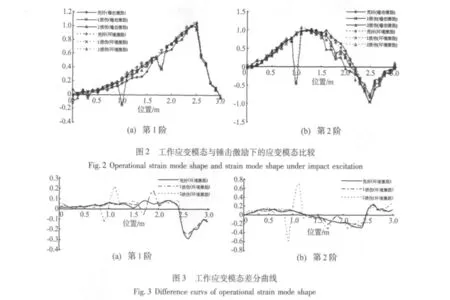
表1 损伤定位指标计算结果Tab.1 Direct index of damage location detection

需要说明的是，根据文献［8］中简支梁数值仿真研究结果，将应变模态差分曲线两极值点间的零点处确定为损伤点。而根据本文悬臂梁损伤状态下模型试验结果，选择两极值点间的中点所对应的位置为损伤点更为合理。该点与零值点位置略有差异，这是由于试验测点不可能非常密集，试验极值点、零值点与理论值会有偏差所致。损伤定位指标计算结果如表1所列。

根据表1可知，除固定支座附近外，完好状态下前2阶最大指标值分别为2.94、1.88；损伤处的指标值在11.24～30.17；损伤非影响区最大指标值在 2.89 ～6.71。损伤处指标值平均是损伤非影响区的4.1倍，远大于非损伤处指标值，且识别出的损伤位置与实际位置一致。所以，根据指标值及应变模态差分曲线分布规律可进行损伤定位。

3.3 损伤程度直接指标

根据图2中的工作应变模态可以发现，在损伤处应变模态值变化剧烈，该处应变模态值明显减小，甚至反向，对损伤状态下出现反向的工作应变模态，如果仍按2.3节损伤程度直接指标法计算，则损伤程度直接指标值会偏大，为此需对该指标法进行改进。在损伤曲线的损伤处作一条水平线，将影响区拟合曲线、影响区左右边界与该水平线所围面积定义为应变模态完好面积；应变模态损伤面积、局域应变模态面积损伤程度指标定义不变。

利用改进后的损伤程度指标法，计算试验工作应变模态损伤程度指标，为了较为全面分析该指标，还对相应数值仿真损伤应变模态曲线进行了计算分析，其中损伤位置、损伤量与模型试验相同。损伤程度指标如表2所列。

表2表明，同一损伤量下的损伤程度指标变化不大，与损伤位置、模态阶数、是否归一化无关；多损伤规律与单损伤相似；试验损伤程度指标值大于数值仿真指标值23%。这主要是由于试验时，测点不可能非常密集，应变模态曲线的渐变性不可能完全反映出来，试验曲线的突变性更为明显，相应的损伤影响区偏小，因而完好面积偏小，损失程度指标也就偏大。

表2 损伤程度指标Tab.2 Direct index of damage degree detection

实际应用时，损伤程度直接指标可根据测点布置的稀疏程度进行折减。对于测点按30等份布置的梁式结构，试验结果偏大23%。一般情况下测点布置越稀，折减系数越大，具体折减规律还要开展进一步的试验研究。

4 结论

（1）本文主要介绍了笔者近几年提出的工作应变模态频域识别方法、基于损伤应变模态差分原理的损伤位置直接指标法、基于局域应变模态面积的损伤程度直接指标法。应变频响函数矩阵任一列包含了应变模态的所有信息，环境激励位移模态试验频域法完全可以应用到应变模态中来。

（2）悬臂梁模型试验及数值仿真计算分析结果表明，利用所提出的方法识别出的工作应变模态与锤击激励下的应变模态形状相似，该方法能较好地识别工作应变模态。

（3）初步验证并完善了损伤位置直接指标法、损伤程度直接指标法。

（4）悬臂梁损伤处损伤位置直接指标值平均是损伤非影响区的4.1倍，远大于非损伤处指标值，且识别出的损伤位置与实际损伤位置一致，所以，根据指标值及应变模态差分曲线分布规律可进行损伤定位。同一损伤量下的损伤程度指标变化不大，与损伤位置、模态阶数、是否归一化无关；试验损伤程度指标值大于数值仿真指标值23%。实际应用时可根据测点布置的稀疏程度进行折减。对于多损伤结构，只要损伤间距大于影响区范围，损伤位置、损伤程度即可按单损伤方法确定。

需要指出的是，本文重点是从多损伤试验的角度初步验证所提方法，某些方面还需进一步完善，今后还要更多地开展不同损伤程度、不同测点间距的损伤直接指标比较研究。

［1］李德葆，陆秋海.实验模态分析及其应用［M］.北京：科学出版社，2001，318 －322.

［2］顾培英，丁伟农.模态试验在梁损伤诊断中的应用研究［J］.振动与冲击，2004，23（3）：60－63.

［3］顾培英，陈厚群，李同春，等.应变模态技术诊断梁结构损伤［J］.地震工程与工程振动，2005，25（4）：50－53.

［4］顾培英，陈厚群，李同春，等.应用应变模态试验技术诊断模型渡槽结构损伤［J］.河海大学学报，2006，34（4）：422－425.

［5］瞿伟廉，陈超，魏文辉.基于应变模态的钢结构构件焊缝损伤定位方法的研究［J］.世界地震工程，2002，18（2）：1－8.

［6］顾培英，邓 昌.基于环境激励下的工作应变模态频域识别方法［J］.振动与冲击，2008，27（8）：68 －70.

［7］顾培英，邓 昌，汤 雷.工作应变模态时域识别方法研究［J］.水力发电，2009，28（5）：27－29.

［8］顾培英，陈厚群，李同春，等.基于损伤应变模态的结构损伤识别直接指标法［J］.自然科学进展，2007，2：240－247.

［9］董 聪，范立础，陈肇元.结构智能健康诊断的理论与方法［J］.中国铁道科学，2002，23（1）：11－24.

［10］刘文峰，柳春图.利用广义应变比能进行结构损伤识别的数值研究［J］.机械强度，2003，2：159－162.

［11］顾培英，陈厚群，李同春，等.基于应变模态差分原理的直接定位损伤指标法［J］.振动与冲击，2006，25（4）：13－17.