环境激励下基础隔震结构的主要动力特性研究

韩建平，王洪涛，刘云帅，杜永峰，李 慧

(1.兰州理工大学 防震减灾研究所，兰州 730050;2.甘肃省土木工程防灾减灾重点实验室，兰州 730050)

基础隔震作为一项成熟的被动控制技术，已得到了大量的应用推广，其良好的隔震性能也已经得到了实际强震的考验。汶川地震中，在邻近普通砖混结构房屋普遍墙体开裂的情况下，采用基础隔震技术的甘肃省陇南市武都区北山邮政职工住宅楼上部结构及隔震层下的下部支承体系完好无损［1］。

按现行规范规定，计算基础隔震结构的水平向减震系数时，应取剪切变形100%对应的等效刚度和等效黏滞阻尼比;罕遇地震验算时，宜采用剪切变形250%时的等效刚度和等效黏滞阻尼比，当隔震支座直径较大时可采用剪切变形100%时的等效刚度和等效黏滞阻尼比［2］。但当结构遭受环境激励或较低水平的地震动影响时，隔震支座的剪切变形远远达不到设计时的水平，从而使得隔震支座的刚度及结构的动力特性与设计时有较大的不同。因此，有必要对基础隔震结构在微幅环境激励下的动力特性及参数进行研究，这将有助于更全面地掌握其在微幅激励作用下的响应特点。目前在这方面的研究尚少，还没有一些非常明确的结论。

本文首先通过对两栋基础隔震建筑在环境激励下的振动测试，运用随机子空间识别法和有理分式多项式法分别识别了结构的模态频率、振型和模态阻尼比。进一步以其中一栋为研究对象，以识别的模态参数作为修正基准，采用多目标优化的方法反演了环境激励下隔震层的实际水平等效刚度。最后基于反演的实际隔震层水平等效刚度对结构的初始有限元模型进行了修正，并对修正后的模型进行了进一步的分析。

1 基础隔震建筑概况及初始有限元模型

本文测试的两栋基础隔震建筑均位于兰州市，一栋为新建的某小学四层公共教学楼，另一栋为已建的某大学书院六层综合教学楼。

限于篇幅，本文主要对某小学公共教学楼的概况及隔震层的布置进行简要描述。该教学楼上部结构为四层钢筋混凝土框架结构，总高度15.6 m，一、二层层高为2.7 m，三层大部分为倾斜楼盖，标高区间为［10.2 11.4］m。该建筑的整体外观如图1照片所示，叠层橡胶隔震支座节点细部如图2照片所示。

该建筑的隔震支座布置如图3所示，图中①、②、③ 分别对应 GZY400、GZY500、GZP600型隔震支座。隔震支座的规格、数量及具体参数如表1所示，其中γ为隔震支座的剪切变形，Kj和ξj分别为相应剪切变形下隔震支座的水平等效刚度和等效黏滞阻尼比。

测试前，为了保证结构现场测试数据的质量，分别建立了所测试结构隔震前和隔震后的初始有限元模型，并对其进行了初步的动力特性分析。

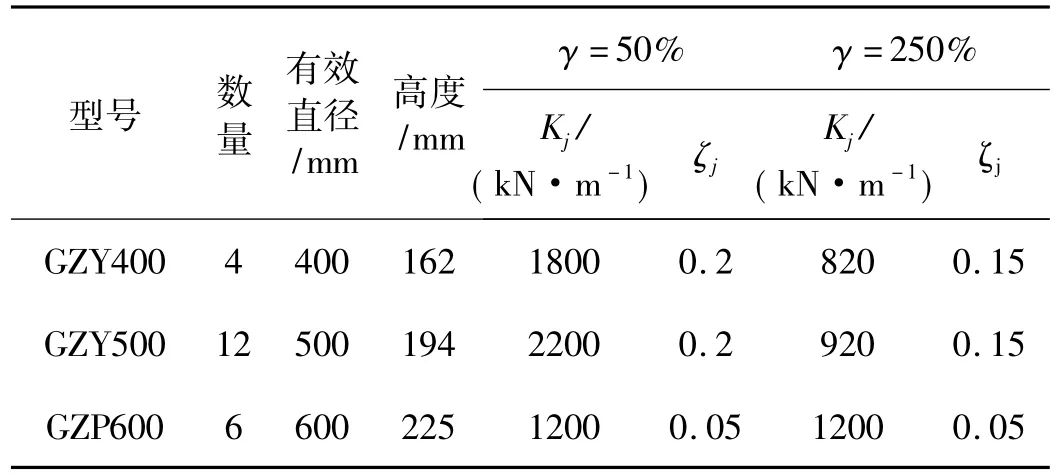
表1 隔震支座的主要参数Tab.1 Main Parameters of rubber bearings

建模过程中作了如下的假定及简化:

(1)结构的质量都集中在各楼层水平面上;

(2)楼板在自身平面内刚度无限大;

(3)考虑到隔震层在小幅环境振动激励下达不到设计剪切变形，隔震层的等效水平刚度初步取为多遇地震设计水平等效刚度的10倍［3］;

(4)将基础隔震支座模拟成有横向刚度和竖向刚度的线单元;

(5)考虑填充墙的刚度贡献，取周期折减系数为0.7。

依据初始有限元模型分析所得的前三阶模态频率及振型形态如表2所示。

表2 初始有限元模型分析所得的前三阶振型Tab.2 First 3 modes from the initial finite element model

2 环境激励下的动力测试

为尽可能地获取结构的横向、纵向和扭转模态，每层布置四个单向水平加速度传感器，在屋面分别设置横、纵向两个参考点。该小学综合教学楼各层测点及参考点的布置如图4所示。

图4 小学公共教学楼测点及参考点布置Fig.4 Locations of traveling and reference accelerometers of public teaching building of the primary school

环境振动下动力测试的基本假设是使引起振动的输入在感兴趣的频率范围内具有白噪声的特性［4］。为了满足这一要求，需尽量减少一些外部因素比如车辆、人员、风、机器等对结构引起的诱使模态，因此选择在相对较安静的深夜进行测试。

测试使用12通道的DASP信号采集和分析系统，采样频率取为80 Hz，采样时间取为20 min，整个建筑的动力测试共分5组。

3 模态参数的识别和分析

模态参数识别的时域方法和频域方法各有其优缺点。环境激励下，频域法使用的是频响函数，虽然输入未知，但是输入为白噪声激励的假定使得可由响应的自功率谱来近似替代频响函数;时域法的初始输入数据是系统的自由衰减响应或脉冲响应，可以通过随机减量技术或者自然激励技术得到。从识别效果上知，时域法无法直接判别是否识别出了系统的所有模态;而频域法虽然可以直观判断模态数量，但是其阻尼比和振型的识别精度较差［5］。

为了增加识别结果的可信度，分别采用时域内的随机子空间法(Stochastic Subspace Identification，SSI)和频域内的有理分式多项式法(Rational Fraction Polynomial，RFP)独立地进行参数识别以对识别结果进行交叉验证［6，7］。

3.1 参数识别

模态参数识别时，选用白噪声激励下各测点纵、横向的数据，其中，SSI法的Hankel矩阵采用方阵构造，系统定阶采用文献［7］中的方法;为解决拟合漏阶的问题，RFP法采用频响函数虚部归一化向量权函数进行拟合识别。模态参数识别结果见表3所示，前三阶振型如图5所示。

利用模态置信准则(Modal Assurance Criterion，MAC)［8］评价SSI和RFP两种方法识别结果的相关性，计算结果见表3所示。两种方法识别的各阶振型的MAC值均在0.75以上，表明两种方法的识别结果有较好的相关性。

表3 模态参数识别结果Tab.3 Identified results of modal parameters

图5 实测所得的小学公共教学楼前三阶振型Fig.5 Identified first 3 mode shapes of public teaching building of the primary school

3.2 有关阻尼识别结果的讨论

一般认为，在基础隔震结构中，由于隔震系统与上部结构的阻尼特性截然不同，它们所组成的整体是典型的非比例阻尼体系［9］。但表3结果表明，在环境激励下，尽管RFP方法识别的阻尼比结果整体略大于SSI方法的识别结果，但两种方法识别所得的隔震结构前三阶振型的阻尼比都相对较小。基础隔震结构的等效黏滞阻尼比的大小近乎于未隔震结构的阻尼比，主要是由于隔震支座在低水平的环境振动激励下，由横向振动所引起的位移和应变都很小，变形橡胶层中的能量损失较小，隔震层对整体结构的阻尼贡献较小［4］。

本次测试中，隔震支座支墩顶部测点与一层楼面处对应测点记录的短向速度时程如图6所示，从中提取的主要时域指标见表4。综合图6及表4结果，两个测点处的速度绝对值都较小，且隔震支座的相对速度值也较小，因此隔震支座提供的阻尼也必然较小。

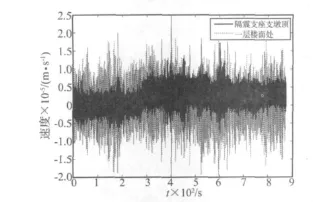
图6 隔震支座上下速度时程图Fig.6 Velocity time history at top and bottom of a rubber bearing

表4 隔震支座上下速度记录的时域统计指标Tab.4 Time domain statistics of velocity record at top and bottom of a rubber bearing

隔震结构在环境激励下未表现出隔震层的高柔性和大阻尼，虽然隔震系统与上部结构的阻尼机制不同，但在环境激励下两者表现出来的阻尼特性没有太大的不同，因此本文在后续分析中将环境激励下的基础隔震结构视为比例阻尼体系。

另外要说明的是，结合表3中阻尼的识别结果以及作者以前所做的一些工作，要比较精准地识别模态阻尼比仍然是比较困难的。对基础隔震结构，阻尼的精确识别对研究隔震支座的耗能机制、隔震结构的非比例阻尼问题等是非常重要的，因此仍然是一个需要进一步研究的问题。国外一些学者提出的瞬时阻尼、阻尼谱［10，11］等一些阻尼识别的新思想，对基础隔震结构阻尼的识别有一定的参考意义。

4 环境激励下隔震层实际水平等效刚度的反演

为了研究隔震支座在小幅环境激励下的刚度与设计刚度取值的不同及其对结构动力特性的影响，也为了进一步修正初始有限元模型以使其可以更好地反映环境激励下基础隔震结构的动力特性及响应，准确、合理地确定隔震层的水平等效刚度是非常重要的。

本文基于环境激励下的实测结果，采用多目标优化的方法来反演环境激励下隔震层的水平等效刚度。

鉴于前述有关环境激励下隔震结构阻尼特性的讨论，采用具有经典比例阻尼的层间剪切模型代表研究的基础隔震结构。假定同层各构件的水平位移一致，忽略柱的轴向变形;将首层下半部分墙体的质量和隔震层的质量集中到隔震支座顶部的楼板上，其它层墙体的质量分别集中于各层楼板及屋面板。

在环境激励下基础隔震结构的运动微分方程为:

式中［K］、［M］和［C］分别为层间剪切型模型的刚度矩阵、质量矩阵和阻尼矩阵;{f(t)}为随机的环境激励。

对无阻尼自由振动体系进行频率和振型计算后，选取前三阶实测频率与计算频率的差的平方和及振型模态置信准则(MAC)的负值为目标函数，建立多目标优化识别隔震层水平等效刚度的数学模型如下:

式中ωei和φei分别为环境激励下实测所得的结构第i阶频率和振型向量;ωai和φai分别为无阻尼层间剪切模型计算所得的第i阶频率和振型向量。

式(3)和式(4)中的［K］和［M］分别取如下的表达式:

其中kb、mb分别为隔震层的等效水平刚度和集中质量;ki、mi分别为第i层(i=1，2，3，4)的层间侧移刚度和集中质量。

为了判断目标函数的总体优化效果，利用线性加权和的方法，分别给表征前三阶模态实测频率与计算频率差值的平方及各阶MAC的负值乘以权系数γi(i=1，2，3)，将式(2)中的目标函数改写为如下形式，则多目标优化问题转化为一维的单目标优化问题［12］。

该优化问题采用经典0.618法求解最优的kb值。

本文讨论的结构隔震层在多遇地震设计水平等效刚度为40 800 kN/m，结合前面的假定，迭代初始区间［kb1，kb2］取为［0.3，0.5］×106kN/m，收敛容差 ε 取0.01。

经迭代计算，得出在环境激励下隔震层的实际水平等效刚度kb=444 720 kN/m，其值为多遇地震设计时所取水平等效刚度的10.9倍，另外该值也大于结构第三层和第四层的层间剪切刚度值。

环境激励下及不同隔震支座剪切变形时基础隔震结构的动力特性对比见表5。

表5 隔震结构动力参数随隔震支座不同剪切变形的变化Tab.5 Dynamic parameters of base-isolated structure with different shear deformation of rubber bearings

表5表明，不同振动幅值时隔震层的等效水平刚度和等效黏滞阻尼比相差较大，结构体系的基本周期相应地也有较大变化。

值得注意的是该建筑设计计算阶段所得的隔震前基本周期为0.460 4 s，大于在环境激励下实测的隔震后周期值0.334 4 s，这固然与隔震层在环境激励下刚度较大有关系，另外理论建模与实际施工之间的差异以及理论建模是否能考虑影响结构动力特性的所有主要因素也是值得进一步研究的。

隔震层在微幅振动激励下的水平等效刚度很大，从结构抗风角度来讲是合理的，可以保证隔震建筑在风振激励下的舒适性能。

5 基于反演隔震层水平刚度的有限元模型修正

将反演所得的隔震层等效水平刚度反馈到初始有限元模型，得到修正后的有限元模型。依据修正后的有限元模型分析所得的前三阶振型的频率及其与试验识别结果及初始有限元分析结果的对比如表6所示。修正后的前三阶振型如图7所示。

表6结果及图5和图7的对比表明，修正后的有限元模型分析所得的频率与试验识别得到的频率吻合较好，两者的振型形状也基本相似，前三阶的MAC值都在0.88以上，表明计算振型与实测振型之间有较好的相关性［13］。

表6 修正前后前三阶模态频率与识别频率的对比及修正后分析模态与识别模态的MACTab.6 Comparison of first 3 frequencies from ambient vibration test，initial model，updated model and MACs between updated modes and identified modes

图7 修正后有限元模型分析所得的前三阶振型Fig.7 First 3 mode shapes from updated finite element model

6 结论

对两栋基础隔震建筑在环境激励下的动力测试及模态参数的识别结果表明，环境激励下基础隔震结构的动力性能与设计分析阶段所考虑的动力性能差别很大，结构的基本周期和模态阻尼比均远小于多遇地震和罕遇地震设计工况下的相应值。因此，为了进一步研究基础隔震结构在环境激励下的动力性能，选择其中一栋为研究对象，利用多目标优化的方法反演分析了隔震层在环境激励下的实际水平等效刚度，反演所得的隔震层水平等效刚度为多遇地震工况下计算刚度取值的10.9倍。最后基于反演的实际隔震层水平等效刚度对结构的初始有限元模型进行了修正，修正后模型的数值分析结果与实际测试结果的对比表明，修正后的模型可以更好地反映结构在环境激励下的动力特性。

另外，测试分析结果也表明，识别所得的隔震结构前三阶振型的阻尼比都相对较小，基础隔震结构的等效黏滞阻尼比的大小近乎于未隔震结构的阻尼比，因此，隔震层对整体结构的阻尼贡献较小，在环境激励等微幅振动影响下，基础隔震结构可以视为经典的比例阻尼系统。

［1］莫 庸，金建民，杜永峰，等.高烈度地震区建筑结构选型问题的初步探讨——5.12汶川大地震陇南地区建筑结构震害考察中结构选型问题的思考［J］.工程抗震与加固改造，2008，30(4):50-55.

［2］GB50011-2010.建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［3］Skinner R I，Robinson W H，Mcverry G H.工程隔震概论［M］.谢礼立，周雍年，赵兴权，译.北京:地震出版社，1996.

［4］ Ventura C E，Finn W D L，Lord J F，et al.Dynamic characteristics of a base isolated building from ambient vibration measurements and low level earthquake shaking［J］.Soil Dynamics and Earthquake Engineering，2003，23(4):313-322.

［5］Han J P，Lu X L，Wang F X.Comparison of modal parameter identification algorithms based on shaking table model test data［C］//The International Society for Optical Engineering，2009:73750K-1-7.

［6］Overschee P V，Moor B D.Subspace identification for linear systems: theory， implementation， applications［M］.Dordrecht:Kluwer Academic Publishers，1996.

［7］ Juang J N.Applied system identification［M］.Englewood Cliffs:Prentice-Hall Inc，1994.

［8］ Allemang R J，Brown D L.A correlation coefficient for modal vector analysis［C］.Proceedings of the First International Modal Analysis Conference (IMAC)， Orlando，Florida;1982.

［9］杜永峰，李 慧，Spencer B F，等.非比例阻尼隔震结构地震响应的实振型分解法［J］.工程力学，2003，20(4):24-32.

［10］ Pines D，Salvino L.Structural health monitoring using empirical mode decomposition and the Hilbert phase［J］.Journal of Sound and Vibration，2006，294(1-2):97-124.

［11］ Ceravolo R.Use of instantaneous estimators for the evaluation of structural damping［J］.Journal of Sound and Vibration，2004:385-401.

［12］明图章，胡光伟，黄 卫.大跨径钢桥面铺装体系多目标优化设计［J］.土木工程学报，2007，40(2):70-73.

［13］任伟新，彭雪林.青洲斜拉桥的基准动力有限元模型［J］.计算力学学报，2007，24(5):609-613.