框剪结构简化振型及在高层建筑风振计算中的应用
张福寿 王国砚
(同济大学航空航天与力学学院,上海200092)
0 引 言
在高层建筑风振计算中,结构的振型具有重要作用,尤其是基本振型,在结构动力响应计算中往往起着主导作用。高层建筑基本振型理论计算的复杂性给其风荷载和风振响应计算带来了很大困难。为便于计算,各国风荷载规范都给出了相应的基本振型简化模型。在我国的现行荷载规范[1]中,采用的是正切函数形式,或者是采用规范中表G.0.3的形式。在美国、日本以及欧洲国家的风荷载规范中,主要是采用幂函数形式,即φ1=(z/H)β[2];其中,美国规范是简单地取 β=1,即采用线性振型[3]。
然而,不同高层建筑基本振型各不相同。有关文献研究表明,直接采用统一的振型表达式计算不同结构的风荷载及风振响应时会产生一定的误差[4-5]。即使日本和欧洲的简化振型表达式中通过对β取不同的值而反映不同结构的振型特点,其形式也过于简单,难以反映不同高层建筑的振型全貌。我国采用的正切函数振型应理解为只适用于偏剪切型结构,梁枢果[4]认为采用正弦函数形式相比于与正切函数能更好反映建筑基阶振型的变化特点;荷载规范表G.0.3给出的振型应理解为适用于偏稍弯曲型结构,况且其表格数据的来源也是值得探究的。
为了便于计算,在进行理论性分析时,一般将高层建筑简化为合理的等效悬臂梁模型来考虑。目前,工程中较多是选用弯剪梁模型或者基于框架剪力墙协同工作原理的模型为简化模型。陈国兴[6]将这两类模型应用于高层建筑随机地震反应分析中,通过具体算例论证了这两种等效梁模型在高层建筑随机地震反映计算中的有效性。Cluni F[7]以这两种模型来估计高层建筑物对风荷载的动态响应,以某高层为算例,经计算对比表明,不管是结构的振型还是风致响应统计特性,两种简化模型与有限元数值模型的结果都具有很好的一致性。然而,由于基于等效梁模型所求得的振型函数解析表达式十分复杂,不便于工程应用。因此,目前很少有学者基于这两类等效梁模型做深入分析并给出基阶简化振型。尽管等效梁模型的振型表达式复杂,但若能通过对方程的求解过程进行分析,得出有利于简化动力特性的相关规律,那么这两种等效梁模型仍将能够得到很好的应用。
文献[8]给出了基于框架剪力墙协同工作原理建立的高层建筑框架剪力墙结构基本振型控制方程和计算方法。本文在此基础上进一步给出高层建筑框剪结构基本振型的形状参数,并对不同参数下的基本振型进行非线性拟合分析,得出了能够更好反映实际结构基本振型且简单实用的振型简化模型;同时本文研究也表明,我国荷载规范中表G.0.3给出的振型属于框剪结构理论振型中λ= 3的情形。
1 基于框剪结构协同工作原理的高层建筑理论振型
根据框架剪力墙协同工作原理,当只考虑剪力墙的弯曲变形和等效框架杆的剪切变形时,高层建筑框架剪力墙结构(以下简称“框剪结构”)的无阻尼自由振动微分方程为[8]

式中:EIW为综合剪力墙的抗弯刚度;C为框剪结构的综合抗剪刚度;m为连续化计算模型的线质量密度。
通过求解方程(1),根据框剪结构连续化计算模型的边界条件,可解得频率方程:

以及振型函数:
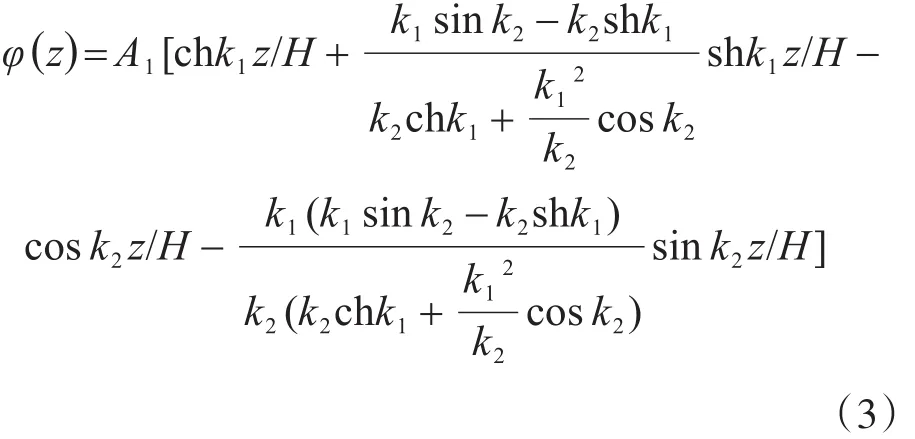
式中:A1为常数;k1,k2为振型参数,它们与刚度特征值λ有如下关系:

令X=z∕H为无量纲高度,并将振型(3)对φ(H)归一化,得到

当λ确定时,联立式(2)和式(4)即可解出k1、k2。求出的k1、k2有无穷多组解,每一组解对应一阶固有频率和振型。将第一组解(k11、k21)代入式(5)即可得到第一阶对应的归一化振型。在整个求解过程中,只要λ值被确定,后续求解任一阶的归一化振型就不再与结构的高度、质量、刚度等参数有关。因此,刚度特征值λ不仅对框剪结构的变形和内力的分配都有很大的影响,而且也是控制任意等截面框架剪力墙以及框架核心筒体系结构等结构体系任一阶振型形状的重要参数,每一阶归一化振型都可归纳为无量纲的相对高度X和λ这两个参数的函数。
现针对第1阶振型(称为基本振型)进行分析。首先对λ从0到40合理地取16个值,并据此确定相应的k11、k21值,其中λ和对应的k11值如表1所示;将k11、k21值代入式(5)即可得到相应的16条归一化的基本振型曲线,如图1(a)所示。可见,随结构体系的不同(反映在λ不同),高层建筑基本振型变化较大。
其中,当λ取 3时,所得振型恰好与荷载规范中表G.0.3给出的振型相吻合,如图1(b)所示。由此可以基本确定,荷载规范表G.0.3中给出的振型即来源于此。

表1 结构特征参数λ与k11H之间的关系Table 1 Relation between structural characteristic parameter λ and k11H
2 本文提出的基本振型简化模型
从以上分析可以看出,式(3)给出的振型表达式的优点在于具有合理的理论依据,且适应各种常见的高层建筑结构体系;缺点是表达式十分复杂,不便于工程应用,因此需要对其进行简化。为检验国外常用简化振型表达式的合理性,本文首先以式(6)作为简化振型


图1 框剪结构基本振型曲线族Fig.1 A set of fundamental mode shape curves of frameshear-wall structures
其中X=z∕H。将β作为待定系数,依次对每一个λ值对应的振型曲线进行拟合,并将拟合结果与式(5)给出的振型曲线(图1(a))进行比较,如图2(a)所示(为了便于观察,由上到下较为均匀地抽取中λ为0、1.5、3、5、10、40对应的拟合效果曲线绘于图中)。由图2(a)可见,选用这一简化振型表达式对偏剪切型的振型拟合效果不太好,也体现不出下弯上剪的振型特点。因此,本文基于相关文献给出的振型表达式,通过变形、组合、退化等处理后发现,采用式(7)的简化振型表达式进行非线性拟合,在各种情况下拟合效果都很好,如图2(b)所示。

3 本文振型幂指数β的确定
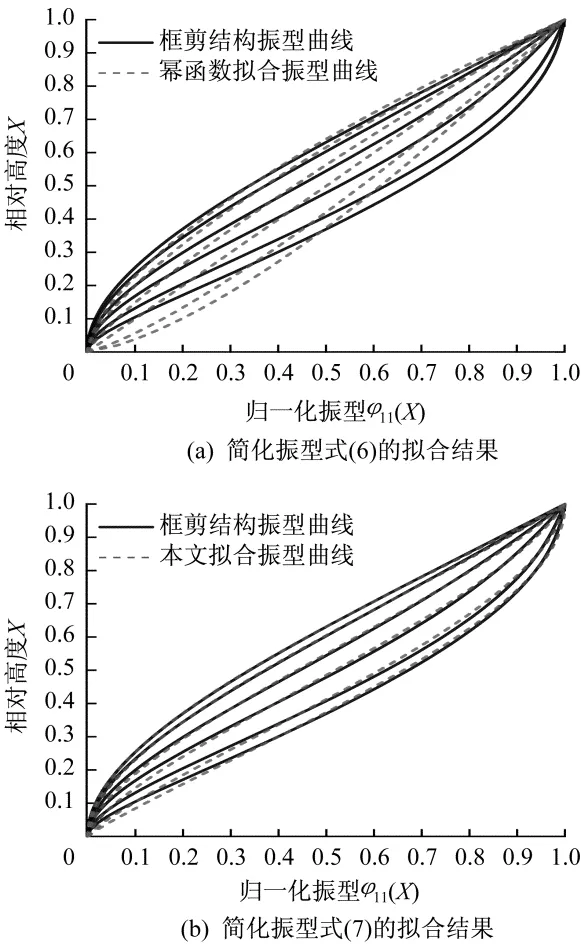
图2 不同简化振型式对框剪结构基本振型曲线族的拟合效果Fig.2 Fitting result comparison between different simplified mode shapes for frame-shear-wall structures
由基于框剪协同工作原理的结构动力特性分析可知,每一个λ对应一条振型曲线,而采用式(7)的简化振型对其拟合时也有相应的一个待定系数值β,λ与β之间存在一定的映射关系。表2给出了振型简化式(7)中的振型幂指数β与λ的对应关系,二者的关系曲线如图3中实线所示。
考虑到β随λ趋于无穷时的收敛性,本文选取反正切函数式(8)来拟合二者之间的近似关系式,拟合效果如图3中的虚线所示。
β(λ)=1.692+0.410arctan(0.837-0.317λ)(8)
由图3可见,采用式(8)计算的β值具有很好的精度,最大误差不超过1.25%。

表2 结构刚度特征值λ与本文振型指数β之间的关系Table 2 Relationship between structural stiffness characteristic number λ and mode index β of this paper
由此,当框剪结构的λ值给定时,代入式(8)得出β值,再将β值代入式(7),可得到与实际结构基本振型十分吻合的简化振型。其中,当λ=0、β=1.95时,为纯弯曲振型;λ取40时与取无穷大时的振型差不多,此时β=1.08,为纯剪切振型;当λ=
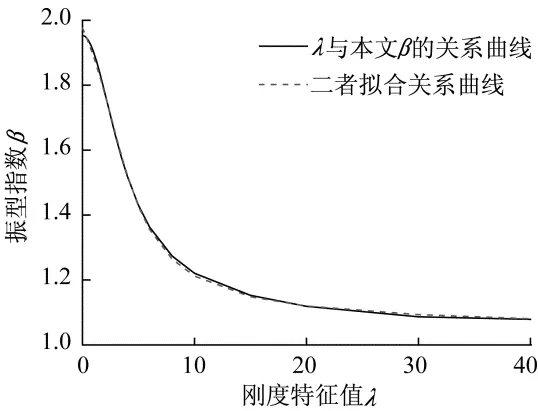
图3 结构刚度特征值λ与本文振型的指数β的关系Fig.3 Relationship between structural stiffness characteristic number λ and mode index β of this paper
3、β=1.807时,所得振型与规范表G.0.3中给出的基本振型吻合。对于剪力墙、框架等其他结构体系,当合理选择参数值时,对应的振型也能与式(7)很靠近。
由式(7)、式(8)和图2(b)可以看出,本文给出的简化振型既具有很好的精度,又具有简洁的表达式和计算方法,便于工程应用。
4 工程算例分析
为了论证本文所提出的基本振型简化模型的准确性,选取三栋横截面较为规则的高层建筑为工程算例,分析选用不同振型对这三栋典型建筑的风致响应计算结果的影响。第一栋建筑是某电梯试验塔,为剪力墙结构体系,建筑共有44层,其中1~3、层为地下室,建筑计算高度为198.9 m;第二栋建筑是某商务中心主楼,为框架剪力墙结构,建筑地面以上共72层,计算高度为290.4 m;第三栋建筑是钢筋混凝土框架结构住宅,结构模型是参考了文献[9]中的算例略作调整所得,建筑地面以上共12层,计算高度为36 m,本文在此基础上添加风荷载,进行风振计算。三栋建筑的具体工程概况如表3所示。
其中阻尼比统一取0.04,体型系数统一取1.4。对于加速度计算,三组算例取基本风压按照10年一遇依次为0.40 kPa、0.45 kPa、0.35 kPa,阻尼比统一取0.02。结构的实际振型和自振周期由有限元法计算得到。结构的等效静力风荷载和结构风振响应均按我国的结构风工程理论和荷载规范条文说明中的精确积分计算式进行计算。

表3 三栋高层建筑的工程概况Table 3 The general situation of three high-rise buildings
对于算例2,结构的刚度特征值λ=3.79,先将λ值代入式(8)得到β=1.549,再将β值代入式(7),得到本文计算的该结构简化基本振型。考虑实际建筑都会含有一定的剪切变形和弯曲变形,因此本文依次取λ=1(β=1.89)、λ=13(β=1.17)为算例1和算例3的基本简化振型。三组算例的振型曲线如图4所示,可见本文给出的简化振型与实际振型都很吻合。
分别采用我国荷载规范[1]中表G.0.3给出的振型和正切函数振型、文献[4]给出的正弦振型、(美国规范采用的)线性振型、本文给出的简化振型,按荷载规范[1]计算这三栋建筑的顺风向风荷载、风致基底剪力、基底弯矩以及顶部加速度,并与采用基于有限元法的结构基本振型计算的相应结果进行比较。比较结果如下:
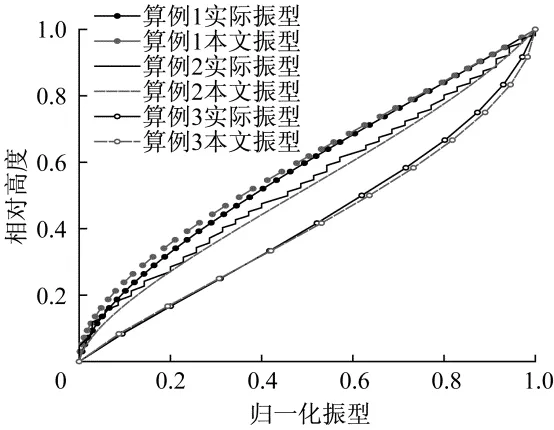
图4 三组算例的振型曲线图Fig.4 Fundamental mode shape curves of the three sets of examples
(1)沿高度变化的风荷载:将根据五种简化振型计算出的沿高度变化的风荷载与根据实际振型计算的结果之间的相对误差列于图5。由图5可见,最大误差依次可达12%、16%、12%、10%、3%,采用本文简化振型计算的风荷载误差最小。

图5 根据五种简化振型计算的风荷载沿高度分布的误差Fig.5 Relative errors of distributed horizontal wind loads calculated in terms of five simplified mode shapes
(2)基底总剪力、基底总弯矩和顶部加速度响应:由表4-表6可看出,在这三组算例中,对于基底剪力,按规范表格振型、正切振型、正弦振型、线性振型计算的最大偏差依次为4.87%、3.49%、4.50%、2.5%;对于基底弯矩,与这四类简化振型对应的结果最大偏差依次为2.78%、1.17%、2.43%、1.02%;对于顶部顺风向加速度响应,最大偏差依次为18.34%、12.64%、10.22%、12.86%。
虽然以往文献的某些简化振型对某一组算例的响应结果可能偏差不大,但综合考虑三组算例,总体偏差还是比较明显。而选用本文的简化振型,不管是对哪一组算例,所计算得到的基底剪力和基地弯矩最大偏差均在1%内;对于顶部加速度响应,最大偏差也很小,不超过1.3%。
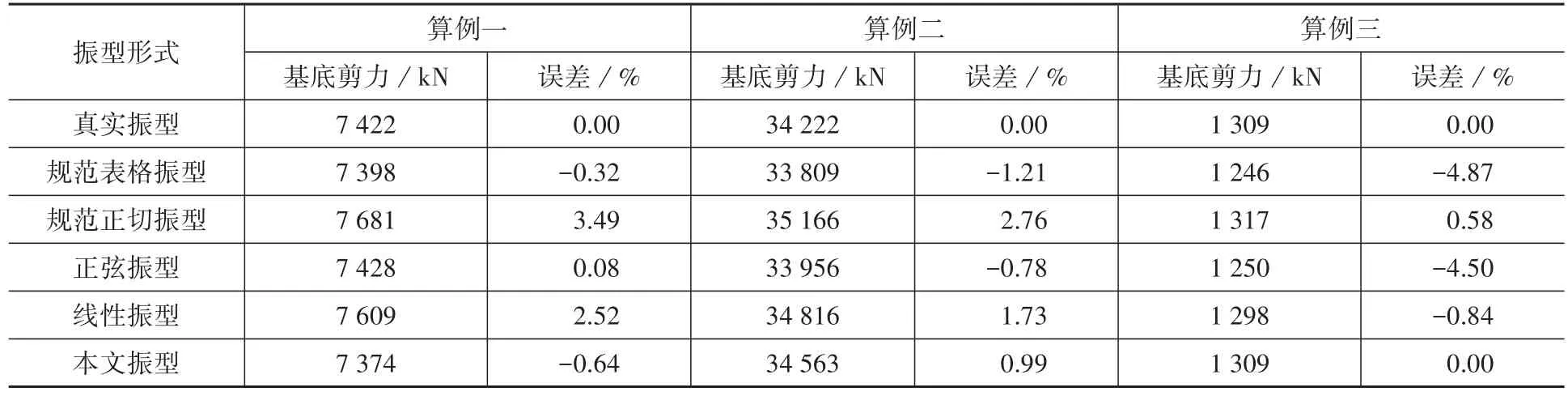
表4 不同简化振型下的基底剪力及其偏差Table 4 Base shear and the relative errors calculated in terms of different simplified mode shapes
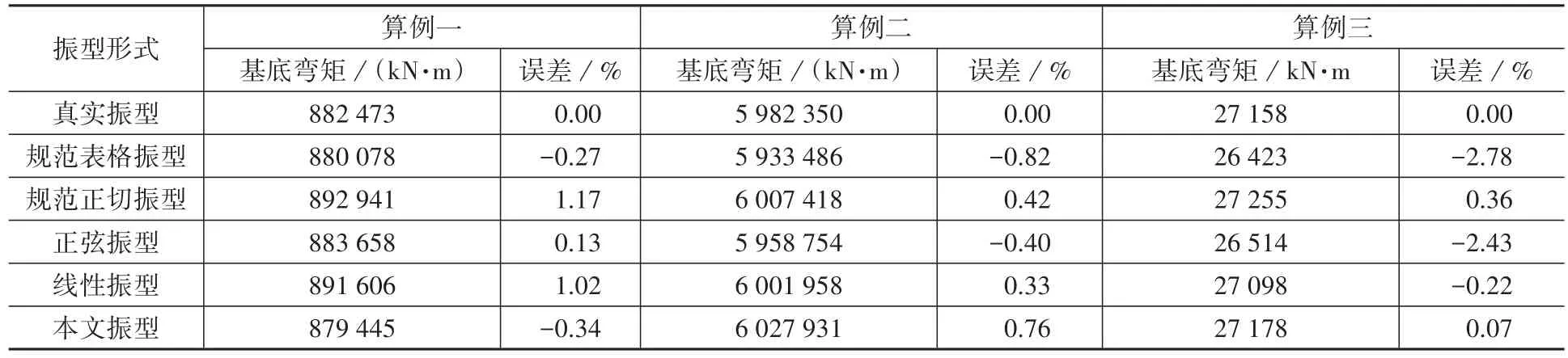
表5 不同简化振型下的基底弯矩及其偏差Table 5 Base moment and the relative errors calculated in terms of different simplified mode shapes
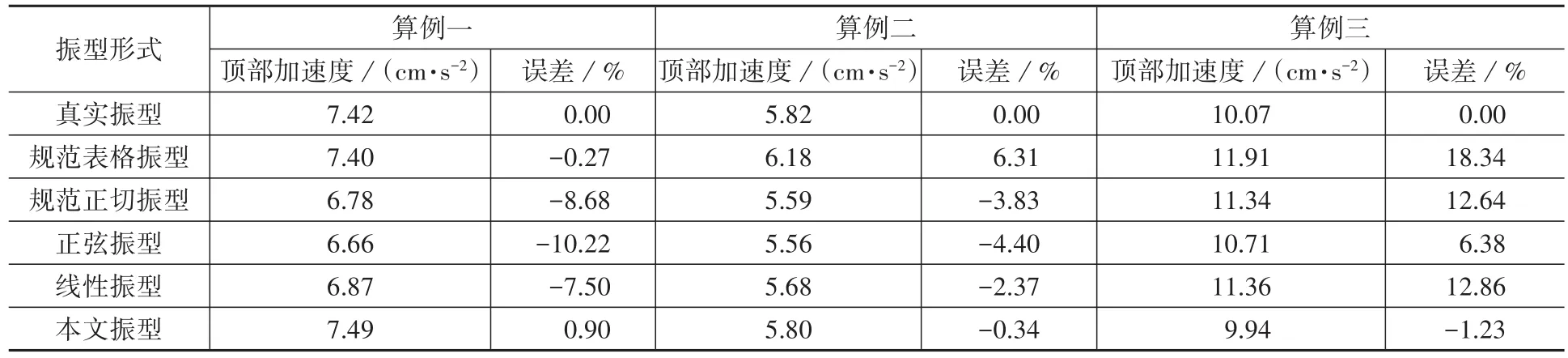
表6 风致顶部加速度响应的计算结果和偏差Table 6 Acceleration and the relative errors calculated in terms of different simplified mode shapes
总体上可以看出,简化振型的不同,对风致响应计算结果会有明显的偏差,尤其对于风荷载分布以及顶部加速度。而采用本文给出的振型,相对能更好地反映建筑的实际振型,从而使风振计算结果的偏差大幅降低。事实上,为验证本文简化振型的适用性,本文从有关资料中收集了10余组由有限元法计算得到的高度在60 m至300 m之间且近似满足等截面均质假定的高层建筑基本振型,采用本文的简化振型对这10组振型进行拟合,结果也很吻合;风荷载和风致响应计算结果的误差也都很小。限于篇幅,在此不一一展示计算结果。
5 结 语
本文在文献[8]的基础上根据高层建筑框架剪力墙结构体系的理论振型归纳出控制框剪结构基本振型形状的参数-结构刚度特征值λ;通过对与不同λ值相对应的理论振型曲线族进行非线性拟合,得出基本振型简化模型,并给出了通过结构刚度特征值λ计算振型指数β的简化方法;最后,将本文简化振型应用到三组实际高层建筑的风荷载和风致响应计算中。
研究结果表明,运用本文简化振型进行高层建筑的风荷载和风致响应计算,能更为准确地反映不同结构体系的基本振型对风荷载计算结果的影响,提高风荷载和结构风致响应的计算精度,且振型表达式简单实用。同时,基于本文的分析可基本确定,我国荷载规范中以表G.0.3给出的振型来源于框剪结构理论振型中λ= 3的情形。此外,可以预料,本文简化振型不仅可应用于高层建筑风致响应计算,而且也可应用于高层建筑抗震设计计算中。
需要说明的是,本文给出的基本振型简化模型只适用于具有任意形状对称截面的等截面匀质高层建筑。对于变截面、具有弯扭耦合效应、非悬臂型等其他形状的高层建筑,则还有待进一步研究。
致谢 感谢同济大学土木工程防灾国家重点实验室全涌教授为本文算例提供的无私帮助。

