考虑运动副间隙的机构动态特性研究

白争锋，赵 阳，赵志刚

（哈尔滨工业大学 航天学院航天工程系，哈尔滨 150001）

由于装配、制造误差和磨损，运动副中的间隙是不可避免的，在机构运行期间，间隙不可避免地存在于各活动铰接处，活动铰关节元素存在失去接触的现象，待再接触时会产生碰撞。间隙使实际机构与理想机构的运动发生偏离，降低了机构运动精度，而且容易引起冲击动载荷，影响系统载荷传递，以及造成运动副的破坏和失效。随着精密机械工程和航天工程的发展，对精确预测系统动力学行为的要求越来越迫切，含间隙机构动力学已经成为国内外机械工程、宇航工程界迫切要解决的关键问题之一［1－5］。为了研究含间隙机构的动态特性，本文建立了一种改进的间隙非线性接触碰撞力的混合模型，同时采用修正的库仑摩擦模型描述间隙处的摩擦作用，并将其嵌入到机械系统动力学分析软件ADAMS中，以含间隙四连杆机构为研究对象，建立含间隙机构动力学模型并进行动力学仿真，详细的研究了含间隙机构的动态特性。

1 含间隙机构动力学建模

运动副铰间间隙会引起相连两体的内碰撞，在机构运行期间，运动副包含有间隙，体与体之间的连接产生了松动，运动副关节元素存在失去接触的现象，进入到自由运动状态，待再接触时会产生碰撞，因此间隙总是要包含着一定的接触和碰撞过程。含间隙机械系统动力学建模的关键是如何把间隙模型嵌入到系统的动力学模型中，这需要考虑间隙运动副的真实描述和间隙接触碰撞过程的正确描述。

1.1 运动副间隙的矢量模型

如图1所示，间隙矢量模型［6，7］通过在平面旋转铰中引入一个间隙矢量来表达旋转铰的真实潜在行为。在该模型中，间隙矢量代表了旋转铰所连接的两相邻构件连接点的精确的相对位置，可以有效处理间隙运动副连接点相对位置的变化。

间隙矢量定义在一个局部浮动笛卡尔坐标系中，以轴承的回转中心为间隙矢量的基准起始点，间隙矢量的方向指向轴和轴承相对运动时的潜在接触点，该潜在接触点构成了轴与轴承的相对碰撞点对。间隙矢量的大小被严格限制在以轴承回转中心为圆心且以轴和轴承的径向尺寸公差为半径的间隙圆内，因此间隙矢量大小的变化能够反映构件的加工误差［6］，并且矢量大小的变化能够反映间隙运动副元素是否接触。

对含间隙旋转铰，间隙大小用轴承与轴半径之差来描述，则间隙为：

图1 运动副间隙矢量模型示意图Fig.1 Revolute joint with clearance

其中Ri为轴承半径，Rj为轴半径。

1.2 运动副间隙的接触碰撞力模型

旋转间隙铰接触碰撞过程中的接触碰撞力模型是含间隙机构动力学分析所必须考虑的重要内容之一。本文建立一种改进的间隙非线性连续接触碰撞力的混合模型，是Lankarani-Nikravesh模型与改进弹性基础接触模型的混合。

Lankarani-Nikravesh模型［8］采用通用的 Hertz接触力表达公式并考虑了阻尼影响且能够描述碰撞过程中的能量损失。其表达式为：

式中，方程右边第一项代表碰撞过程的弹性变形力，第二项则描述了碰撞过程中的能量损失行为，式中的K为碰撞体的接触刚度系数，由Goldsmith通过两个球形体的碰撞实验测得，其表达式为：

其中v和E分别表示泊松比和杨氏模量，Ri和Rj分别为两球的半径。

式（2）中的系数D为碰撞过程的阻尼系数，为相对碰撞速度，D的表达式为［8，9］：

其中ce为恢复系数；（－）为撞击点的初始相对速度。

由于式（3）阻尼系数的推导过程中假设恢复系数ce≈1，所以得到的表达式只能表示大的恢复系数，而无法表示小的恢复系数，文献［10］对此作了改进，得到了修正后接触阻尼与恢复系数之间的关系如式（4），该阻尼系数不受碰撞恢复系数的限制。

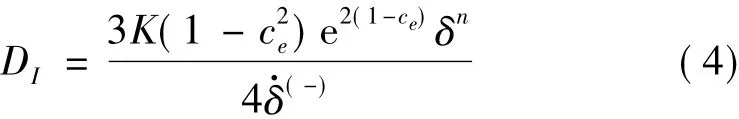
由于Hertz接触理论是基于凸面与凸面的接触问题推导出来的，并且在处理大间隙非协调接触中是可以得到令人满意的结果的，然而实际旋转铰中间隙很小，并且是凸面与凹面的接触，尤其在小间隙轴孔接触时，得到的结果往往是不精确的。而且在以往的大部分文献中，碰撞接触刚度和阻尼系数都是根据两个球形体碰撞情况简单计算甚至根据经验取一个常值，这和实际情况是不相符的［11－13］。文献［11］采用了Winkler弹性基础模型以及Hertz的二次压力分布假设，提出新的适合描述圆柱间隙铰的载荷－位移关系，得到了基于改进弹性基础模型的圆柱间隙铰载荷FN与变形量δ的关系如下：

其中式（5）中E*为复合弹性模量，表达式为：

该模型不仅能应用于有较大间隙情况的接触问题，也能应用于有较小间隙情况的接触分析，拓展了间隙接触分析。通过与有限元数值计算结果对比，发现该简化模型比目前通常采用的Hertz模型具有更好的精度及更大的适用范围［11］。

本文在其基础上，提出了非线性刚度系数，通过求解基于改进弹性基础接触模型的间隙铰载荷－位移关系曲线在某瞬时碰撞点附近的曲线斜率得到［14］，由式（5）进一步可以得到非线性刚度系数Kn为：

间隙接触碰撞力模型的改进主要是在弹性接触力基础上增加某种形式的阻尼力，采用文献［15］中的研究思想，以及结合基于改进弹性基础模型的间隙铰接触碰撞力表达式，对式（4）阻尼形式进一步改进，在阻尼力模型中引入基于改进弹性基础接触模型推导的非线性刚度系数与Lankarani-Nikravesh模型刚度系数之比，则阻尼系数如下：

在以上研究基础上，本文采借鉴文献［15］中的研究思想，建立Lankarani-Nikravesh模型与基于改进弹性基础接触模型的混合模型，采用Lankarani-Nikravesh模型的形式，模型中的刚度系数应用基于改进弹性基础接触模型推导的非线性刚度系数Kn，以及在Lankarani-Nikravesh模型的阻尼力中引入改进弹性基础接触模型与Lankarani-Nikravesh模型刚度系数之比，从而混合模型碰撞过程中的阻尼系数为Dmod。因此运动副间隙接触碰撞力混合模型的表达式为：

1.3 运动副间隙的摩擦力模型

运动副间隙切向接触特性可以通过切向摩擦力模型来描述，本文考虑运动副间隙摩擦为干摩擦，不考虑润滑。最为著名的摩擦力模型是Coulomb摩擦模型，该模型通常用于描述冲击或接触碰撞过程中的摩擦行为。为了能够更加准确描述轴与轴承间的干摩擦行为，以及相对低速情况下出现的粘质和微滑现象，避免数值计算中速度方向变化时出现摩擦力突变，本文采用修正的Coulomb摩擦力模型，在该模型中提出了动态摩擦系数的概念，即摩擦系数不是一个常数，而是与切向滑动速度有关，是切向滑动速度的函数，切向摩擦力计算公式为：

在该模型中提出了动态摩擦系数的概念，即摩擦系数不是一个常数，而是与切向滑动速度有关，是切向滑动速度的函数，其公式表达为：

其中νt表示轴与轴承在碰撞点的相对滑动速度，即切向方向的速度分量，μd为滑动摩擦系数，μs为静摩擦系数，νs为静摩擦临界速度，νd为最大动摩擦临界速度。在区间［0，νd］采用heaviside阶跃函数的三次多项式逼近。

动态摩擦系数的函数曲线如图2。

2 含间隙机构动态特性仿真分析

2.1 机构仿真参数

基于上述含间隙运动副的间隙矢量模型和间隙接触碰撞力的混合模型，以及修正的摩擦力模型，将其嵌入ADAMS软件中，以一四连杆机构为对象，建立含间隙四连杆机构动力学模型并进行动力学仿真分析，研究含间隙机构动态特性。

图2 摩擦系数随滑动速度的变化曲线Fig.2 Coefficient of friction vs.slip velocity

图3 含间隙四连杆机构Fig.3 4 － bar mechanism with joint clearance

四连杆机构如图3所示，连杆与随动杆的转动铰B存在间隙。四连杆机构的参数如下：曲柄l1=550 mm，连杆l2=360 mm，随动杆l3=640 mm，支架l4=210 mm，m1=3.625 3 kg，J1=0.102 143 kg·m2，m2=2.439 4 kg，J2=3.142 8 × 10－2kg·m2，m3=4.189 4 kg，J3=0.157 96 kg·m2，间隙大小为 0.5 mm，摩擦系数为0.1，恢复系数为 0.9，杨氏模量为 207 GPa，曲柄转速为600 r/min。

2.2 仿真结果与分析

为了研究运动副间隙对机构运动特性的影响，取间隙为c=0.5 mm，对含间隙机构与理想不含间隙机构进行动力学仿真，随动杆的动力学特性结果如图4。

由图4（a）可知，含间隙时随动杆的角位移与理想铰时随动杆的角位移曲线几乎完全重合，这表明间隙对机构的角位移基本没有影响。由图4（b）可知，考虑铰间间隙时，随动杆的角速度围绕理想无间隙随动杆角速度出现小的波动，但整体趋势相同，说明铰间间隙对随动杆的角速度影响较小。然而，由图4（c）可知，理想机构随动杆角加速度曲线很光滑，但考虑铰间间隙时，角加速度出现明显的波动，存在许多峰值，并且幅值比理想机构增大，可知铰间间隙对随动杆的角加速度有较大的影响，对机构的运动精度产生较大的影响。分析可知由于轴与轴套之间存在间隙，因此产生了间隙碰撞力，是一种局部效应，每次碰撞时间极短，因此对角位移影响不大，但对角加速度影响较明显。间隙碰撞力如图5所示，由于间隙的存在，产生了脉冲式的间隙碰撞力，碰撞力幅值较大并且体现出高频振荡的特点。维持曲柄恒速转动所需的驱动力矩也体现出相同的特点，如图6所示。

图4 含间隙机构动态特性Fig.4 Dynamic Characteristics of Mechanism with joint clearance

图5 关节碰撞力Fig.5 Contact force in the joint

将本文改进的间隙非线性连续接触碰撞力模型与基于Lankarani-Nikravesh模型进行含间隙机构动态特性仿真结果进行比较，基于Lankarani-Nikravesh模型的仿真结果如图7所示。

图6 维持曲柄恒转速所需的驱动力矩Fig.6 Crank moment required to maintain the angular velocity constant

图7 Lankarani-Nikravesh模型仿真结果Fig.7 Simulation results of Lankarani-Nikravesh model

比较图7与图4（c）、图5可以看出，基于Lankarani-Nikravesh模型计算含间隙机构动态特性时，机构稳态工作时，加速度和碰撞力振荡的更厉害，振荡幅值更大。

进一步基于本文模型研究不同间隙大小对机构动态特性的影响，取间隙大小分别为0.25 mm，0.1 mm，0.01 mm进行动力学仿真分析，随动杆加速度曲线的仿真结果如图8。

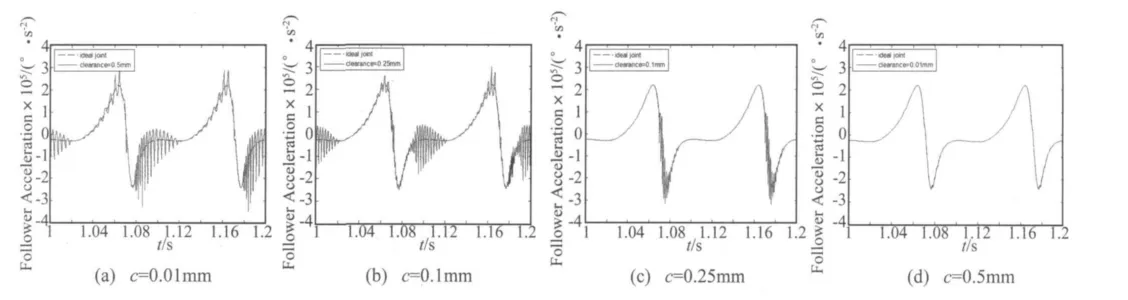
图8 不同大小间隙机构动态特性Fig.8 Dynamic Characteristics of Mechanism with different clearance size

由分析图8可知，不同间隙大小时，随动杆的动态特性差别很大。具体表现为：间隙越小，对随动杆角加速度的影响降低，波动幅值变小，因而间隙越小，铰间间隙碰撞力波动峰值越小。因此当铰间间隙减小时，机构动态行为曲线变得更加光滑，表现为有较小的波动峰值，并且间隙越小，系统的动力学特性更趋向于理想机构。

3 结论

由于装配、制造误差和磨损，运动副中的间隙是不可避免的，在机构运行期间，间隙不可避免地存在于各活动铰接处，间隙使实际机构与理想机构的运动发生偏离，降低了机构运动精度。为了讨论间隙对机构动力学特性的影响，本文建立了一种改进的间隙非线性连续接触碰撞力的混合模型，并采用修正的库仑摩擦模型描述间隙的摩擦作用，并将其嵌入到机械系统动力学分析软件ADAMS中，以含间隙四连杆机构为研究对象，建立含间隙机构动力学模型并进行动力学仿真，详细的研究了含间隙机构的动态特性。研究结果表明：

（1）间隙的存在使得机构的动态特性发生变化，具体表现为：对机构的角位移没有影响；对机构的角速度有较小的影响；对机构的角加速度有较大的影响，角加速度出现明显的波动，并且幅值比理想机构增大；因此间隙对机构的运动稳定性影响较大，也说明角加速度对间隙比较敏感。间隙的存在会增大运动副关节碰撞力，产生脉冲式的接触碰撞力，碰撞力呈现出高频振荡的特点；

（2）间隙减小时，机构动态行为曲线变得更加光滑，表现为有较小的波动峰值，并且间隙越小，系统的动力学特性更趋向于理想机构。

（3）考虑运动副间隙的机构更加真实的反映了机构的动力学特性，能够准确的预测含间隙机构的动力学特性，为研究机构的运动精度和机构设计提供了基础。

（4）本文建立的改进的间隙非线性连续接触碰撞力的混合模型能够有效的描述含间隙机构的动态特性，并且计算效率较高，拓展了间隙铰接触碰撞动力学建模与含间隙机构动力学特性的研究，有利于工程实际应用。

［1］Flores P，Ambrosio J，Claro P.Dynamics Analysis for Planar Multibody Mechanical Systems with Lubricated Joints［J］.Multibody System Dynamics，2004，12：47 －74.

［2］Bauchau O A，Rodriguez J.Modeling of Joints with Clearance in Flexible Multi-body System ［J］.International Journal of Solids and Structures，2002，34：41 －63.

［3］Garcia Oeden J C.Analysis of clearance in multibody system［J］.Multibody System Dynamics，2005，13：401 －420.

［4］白争锋，赵 阳，田 浩.含铰间间隙太阳帆板展开动力学仿真［J］.哈尔滨工业大学学报，2009，41（3）：11－14.

［5］刘才山，陈 滨.多柔体系统动力学碰撞研究中的若干基本问题［J］.振动与冲击，1999，18（3）：5 －12.

［6］时 兵，金 烨.面向虚拟样机的机构间隙旋转铰建模与动力学仿真［J］.机械工程学报，2009，45（4）：299－303.

［7］ Flores P，Ambrosio J，Claro H C P，et al.A study on dynamics ofmechanicalsystems including joints with clearance and lubrication ［J］.Mechanism and Machine Theory，2006，41：247－261.

［8］Lankarani H M，Nikravesh P E.A contact force model with hysteresis damping for impact analysis of multibody systems［J］.Journal of Mechanical Design.1990，112：369 －376.

［9］ Flores P，Ambrosio J，Claro J C P，et al.Influence of the contact impact force model on the dynamic response of multibody systems［J］.Proceedings of the Institution of MechanicalEngineers，PartK： JournalofMulti-body Dynamics，2006，220（1）：21－34.

［10］秦志英，陆启韶.基于恢复系数的碰撞过程模型分析［J］.动力学与控制学报，2006，4（4）：294 －298.

［11］ Liu C S，Zhang K，Yang R.The FEM analysis and approximate model for cylindrical joints with clearances［J］.Mechanism and Machine Theory，2007，42：183 －197.

［12］陈鹿民，阎绍泽，郭 峰，等.多柔体系统动力学中的间隙接触内碰撞［J］.精密制造与自动化，2003，（增刊）：65－67.

［13］ Liu C S，Zhang K，Yang L.Normal force-displacement relationship of spherical joints with clearances［J］.Journal of Computational and Nonlinear Dynamics，Transactions of the ASME，2006，（1）：160 －167.

［14］ Ravn P.A continuous analysis method for planar multibody systems with jointclearance［J］. Multibody System Dynamics，1998，2：1 －24.

［15］ Koshy C S.Characterization of mechanical systems with real Joints and flexible links ［D］. Wichita State University，2006.