串联隔震系统水平刚度及对结构地震响应影响

杜永峰，朱前坤，李 慧

（1兰州理工大学 防震减灾研究所，兰州 730050；2兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050）

隔震建筑普遍采用由叠层橡胶支座和地下室悬臂柱组成的串联隔震系统，如图1所示。叠层橡胶支座由薄橡胶片与钢板分层叠合而成，具有很大的竖向刚度、较小的水平刚度和很大的变形能力，其中在压应力作用下具有较小的水平刚度是其最重要的力学性能［1］。Gent［2］最早基于 Haringx 理论研究了叠层橡胶支座的力学性能。Koh和Kelly［3］为了简化计算提出了双自由度力学模型，分析了叠层橡胶支座在大水平位移时的力学性能。Nagarajaiah等［4］改进Koh－Kelly双自由度力学模型得到了更精确的临界荷载和水平刚度，Buckle［5］用试验验证了改进模型的有效性。随着高层隔震建筑的大量出现，Kelly和 Warm等［6，7］分析了叠层橡胶支座的竖向刚度和拉伸屈曲。Liu和 Yang［8，9］提出隔震支座的一些基本概念，较为系统的建立了隔震支座各种力学性能的计算理论和评价方法。王建强等［10］研究了上部结构（偏心）对基础滑移隔震结构平－扭耦联地震反应的影响。周锡元、韩淼等［11，12］在Harings和Gent研究基础上建立了柱串联隔震系统的分析模型，推导出柱串联隔震系统的水平刚度计算公式及临界荷载求解公式。近20年来的几次强烈地震中，在近场记录到了较强的竖向地震动，部分场点记录到的竖向峰值远超过水平向峰值［13］，故应考虑压应力对柱串联隔震系统水平刚度的影响。本文在前人研究的基础上，基于传递矩阵法［14］，推导出隔震系统端部状态变量与任意截面的内力和位移值之间的关系，可以较容易地得到单个橡胶支座和串联隔震系统水平刚度计算公式，避免了繁琐的力学推导过程，并探讨了压应力对水平刚度及结构地震响应的影响。

图1 串联隔震体系模型Fig.1 Series isolation system model

图2 橡胶支座隔离体Fig.2 Isolation rubber bearing body

1 传递矩阵

柱串联隔震体系分析模型如图1所示的。忽略轴向变形，h1、h2分别是叠层橡胶支座与地下室柱的高度，δ为隔震支座顶端的水平位移。以叠层橡胶支座为研究对象，截取高度为x（0＜x＜h1）的隔离体，其受力与变形如图2所示。δ0、φ0、F0、M0和P分别是橡胶支座顶水平位移、挠度角、水平力，弯矩和轴向力，δ（x）、φ（x）、M（x）和δ'（x）－φ（x）分别是橡胶支座任一截面截面x处水平位移、挠度角、弯矩和剪切应变，V（x）和N（x）分别平行和垂直于x截面的剪力和轴力，则本构方程为：

式中kb和ks分别为橡胶支座等效弯曲刚度和剪切刚度［15］：

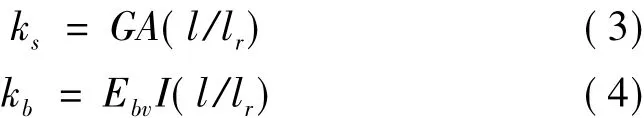
式中l为橡胶支座的总高度，lr为橡胶支座中橡胶的总厚度，Ebv=EvEb/Ev+Eb为橡胶支座的修正弹性模量，Ev为橡胶材料的体积弹性模量，Eb=3G（1+2/3）为橡胶支座的弯曲弹性模量，G为橡胶材料的剪切模量，κ为剪切模量相关的修正系数，S1=D/4tr为橡胶支座的第一形状系数，S2=D/lr为橡胶支座的第二形状系数，D为支座直径，tr为单层橡胶片厚度。

由文献［6，11，12］可得隔离体的任意截面的内力和位移：

式中参数有下式确定

令x=0，由式（5）和式（8）可得：

把式（9）代入式（5）～式（8）可得：

把式（10）～式（13）写成以下矩阵形式：

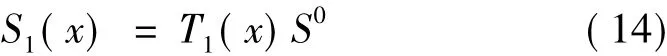
式中：

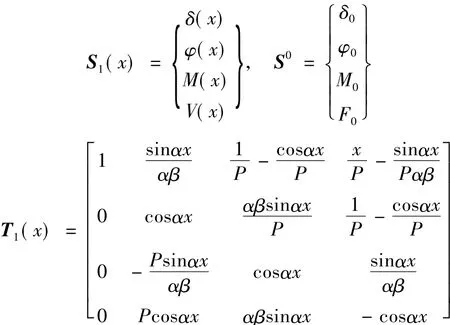
式中：S0为初始状态变量，S1（x）为x截面状态变量，T1（x）为传递矩阵。由式（14）知，如果初始状态变量已知，就可以容易求出橡胶隔震支座任意截面处的变形和内力。

2 水平刚度

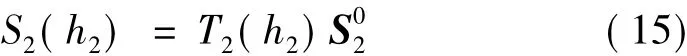
式中：T2（h2）为地下室柱的传递矩阵。

橡胶隔震支座与地下室柱交界面应满足：

式（16）代入到式（15）可得：

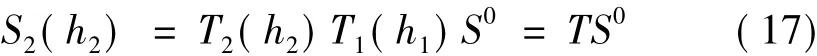
令γ1=α1β1，γ2=α2β2，η1=sinα1h1，η2=sinα2h2，λ1=cosα1h1，λ2=cosα2h2

α1、β1和α2、β2分别表示橡胶隔震支座与地下室柱的有关参数，分别可按下式确定：

则式（17）中：

在实际工程中橡胶支座上端纵横向连接梁刚度比橡胶支座刚度大的多，可认为支座上端的转角为零即φ0=0，地下室柱固定在基础上即δ（h1+h2）=0和φ（h1+h2）=0展开式（17）前两式，得：

把式（19）代入式（18）可得：

式（20）变形可得：

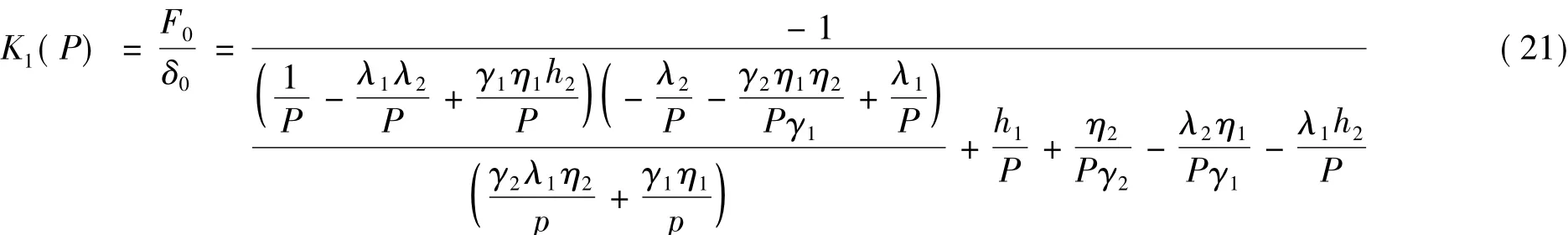
式（21）即为串联隔震体统水平刚度计算公式。

同理得到隔震支座的水平刚度的计算公式：

式（22）与文献［5］给出的水平刚度计算公式相同。

3 算例分析

考查实际工程中由混凝土强度等级为C30、截面尺寸为600 mm×600 mm、高为1 500 mm的地下室悬臂柱和橡胶隔震支座GZP 500组成串联隔震系统。隔震支座参数：直径为500 mm、高度为164 mm、橡胶片层厚4.87 mm、第一形状系数为30、橡胶剪切模量为0.6 GPa。图3所示为单个橡胶支座和串联隔震系统的水平刚度和压应力的关系。从图3中可以看出水平刚度随着压应力增加而减小；当压应力不大即竖向地震不明显时，单个橡胶支座和串联隔震系统的水平刚度比较接近，随着压应力增加两者差值逐渐增大；当水平刚度为零时，相应压应力即为临界压应力，从图3中串联系统临界压应力要比单个橡胶支座小10%左右。

图3 水平刚度与压应力的关系Fig.3 The relation between horizontal stiffness and compressive press

隔震支座GZP 500设计压应力为15 MPa，水平刚度取压应力值为设计值1.5倍的对应值。采用隔震支座直接固定在基础上方案A结构参数：1到3层的质量分别为 742 700 kg、788 500 kg、468 100 kg，水平刚度分别取为44 100 kN/m、407 780 kN/m、282 500 kN/m；采用串联隔震系统方案B结构参数：1到3层的质量分别取为 742 700 kg、788 500 kg、468 100 kg，水平刚度分别取为42 160 kN/m、407 780 kN/m、282 500 kN/m。利用非比例阻尼隔震结构地震响应的实振型分解法方法［16］，采用加速度峰值为4 m/s2的kobe波，计算隔震建筑的地震响应。图4为隔震建筑底层在地震作用下动力响应。A方案底层最大层间位移、绝对最大加速度、最大基底剪力分别为 93.98 mm、1.937 m/s2和 3 975 kN；B 方案分别为 93.19 mm、1.928 m/s2和 3 962 kN。可见采用隔震方案A和B结构地震响应几乎相同。把不同压应力相对应水平刚度值带入动力方程求解，得到隔震结构底层不同的剪力时程曲线，取出其绝对最大值。图5所示即为最大基底剪力与压应力的关系曲线，关系曲线表明当压应力不是很大即竖向地震作用不显著时，采用两种不同隔震方案的基底剪力大致相同；随着压应力的增加即竖向地震作用加大，隔震层水平刚度不断降低即承受水平荷载能力也不断降低，当压应力增加到62.63 MPa时，串联隔震系统达到临界应力，水平刚度为零即丧失承受水平地震作用的能力，而采用隔震支座直接固定在基础上的隔震方案还具有继续承受水平地震的能力。因此在竖向地震作用比较明显近断层建议采用支座直接固定在基础上的隔震方案。

图4 隔震结构底层的地震响应Fig.4 Seismic response of the bottom layer of isolated building

图5 最大基底剪力与压应力关系Fig.5 The relation between the maximum base shear and compressive press

4 结论

本文基于传递矩阵法建立了串联隔震系统的水平刚度计算公式，并利用非比例阻尼隔震结构地震响应的实振型分解法方法对比分析了采用不同隔震方案的地震响应，得到的主要结论如下：隔震层的水平刚度随着压应力的增大而减少，所以在近断层可能因为较大的竖向地震作用而引起隔震层丧失水平承载能力，建议采用支座直接固定在基础上的隔震层方案；在压应力不大即竖向地震不明显的地区，串联隔震体系和单个支座的水平刚度相差不大，采用以上两种隔震方案的隔震结构地震响应也相差不大，故采用串联隔震体系的隔震方案。

［1］Herrmann LR，RamaswamyA，HamidiR. Analytical parameter study for class of elastometric bearings［J］.Journal of Structural Engineering，1989，115（10）：2415 －2434.

［2］ Gent A N.Elastic stability of rubber compression springs［J］.Journal of Engineering Mechanics，1964，6（4）：318 －326.

［3］Koh C G，Kelly J M.A simple mechanical model for electrometric bearings used in base isolation［J］.Journal of Engineering Mechanics，1988，30（12）：933 －943.

［4］Nagarajaiah S，Ferrell K.Stability of electrometric seismic isolation bearings［J］.Journal of Strutural Engineering，1999，125（9）：946－954.

［5］ Buckle I，Nagarajaiah S，Ferrell K.Stability of electrometric isolation bearings： Experimentalstudy［J］. Journalof Strutural Engineering，2002，128（1）：3 －11.

［6］Kelly J M.Tension buckling in multilayerelastomeric bearings［J］.Journal of Engineering Mechanics，2003，129（12）：1363－1368.

［7］Warm G P，Whittaker A，Constantinou M.Vertical stiffness of electrometric and lead-rubber seismic isolation bearings［J］.Journal of Strutural Engineering，2007，133（9）：1227－1236.

［8］ Liu W G，He W F，Feng D M，et al.Vertical stiffness and deformation analysis models of rubber isolators in compression and compression-shear states［J］.Journal of Engineering Mechanics，2009，135（9）：945 －952.

［9］ Yang Q R，Liu W G，He W F，et al.Tensile stiffness and deformation model of rubber isolators in tension and tensionshear states［J］.Journal of Engineering Mechanics，2010，136（4）：429－437.

［10］王建强，丁永刚.上部结构（偏心）对基础滑移隔震结构平－扭耦联地震反应的影响［J］.振动与冲击，2009，28（12）：96－100.

［11］周锡元，韩 淼，曾德民，等.橡胶支座与R/C柱串联隔震系统水平刚度系数［J］.振动工程学报，1999，12（2）：157 －165.

［12］周锡元，韩 淼，曾德民，等.组合橡胶支座及橡胶支座与住串联系统的水平刚度计算方法［J］.地震工程与工程振动，1999，19（4）：67 －75.

［13］李 恒，黄 江，罗等贵.竖向地震动加速度峰值统计特性［C］.纪念汶川地震一周年－地震工程与减轻地震灾害研讨会论文集.北京：地震出版社，2009：150－156.

［14］刘庆潭.材料力学教程［M］.北京：机械工业出版社，2006：313－321.

［15］周福霖.工程结构减震控制［M］.北京：地震出版社，1997：85－86.

［16］杜永峰，李 慧，Spencer B F J等.非比例阻尼隔震结构地震响应的实振型分解法［J］.工程力学，2003，20（4）：24 －32.