不同荷载作用下T形连续梁和悬臂梁的剪力滞效应

赵明岩，董毓利，雒家琪

(华侨大学 土木工程学院，福建 厦门 362021)

T形截面在高层建筑及桥梁结构中有广泛应用.然而，荷载作用时，由于腹板剪应力在翼板不均匀分布，导致翼板存在剪力滞后现象，使得截面应力分布不均匀.自Reissner应用最小势能原理分析了单箱截面剪力滞效应以来，国内外的剪力滞效应研究成果逐渐丰富[1]，研究方法也较多.文献[2]考虑了弯、扭、剪力滞耦合的有限段模型；文献[3]以薄壁杆理论和有限元法为基础，提出了薄壁箱梁考虑剪力有限段法.对于连续梁和悬臂梁，集中荷载和均布荷载作用时，将出现负剪力滞现象[4-5].文献[6]解释了正负剪力滞产生的原因，文献[7]分析了曲线箱梁箱梁的剪力滞效应.

滞效应自由振动特性分析的 事实上，只要梁截面存在肋板构件，就会导致剪力滞现象.对于剪力滞效应而言，有很多影响因素，如宽跨比、梁高比[8]、荷载形式[9]、温度[10-11]、梁端约束[12]，以及荷载作用[13]位置等因素都会影响剪力滞效应.工程中在计算截面应力时，大多依旧采用平截面假定，不考虑腹板的剪切变形，中性轴位置按初等梁理论计算的位置.实际荷载作用时，梁翼板的位移会出现不同剪力滞效应，当翼板与腹板交接处的正应力大于按初等梁的计算值，称为正剪力滞，反之为负剪力滞[14].

目前有关T形截面剪力滞效应的研究较少，多以箱梁为主.文献[15-16]用非线性有限元知识，分析T梁的计算模型，对T梁受力过程进行数值分析；文献[17-18]则以钢筋混凝土结构及预应力混凝土为主要测试构件，分析集中荷载作用下的剪力滞效应.本文以有机玻璃为研究材料，对比分析不同荷载形式剪力滞效应传递规律，以及不同梁种类的剪力滞效应对比，分析剪力滞效应.

1 T形梁剪力滞试验

为研究集中荷载和均布荷载作用下有机玻璃T形连续梁和悬臂梁的剪力滞效应，根据JTG D60-2015《公路桥涵设计通用规范》[19]，参考文献[20]的试验模型，设计T形梁全长为1 800 mm，腹板高为72 mm，腹板宽为10 mm，翼板宽为200 mm，翼板厚为8 mm.T梁在放置时不具稳定性，故在T梁两端和跨中分别设有25 mm厚隔板，增强连续梁的稳定性.由于支座反力存在，隔板对于应变的影响是全截面，但对于应变的变化趋势影响较小.

T形梁试验模型尺寸及测量截面，如图1(a)所示.模拟连续梁铰支座采用圆形钢，将T梁隔板部位放置在上方，如图1(b)所示.模拟悬臂梁固定端的用钢板将T梁翼板上方固定，钢板两侧用螺栓将钢板与下方钢架固定，如图1(c)所示.选用有机玻璃代替混凝土，因为相比混凝土，有机玻璃与应变片连接更紧密，使应变测量更加准确，且有机玻璃与混凝土力学性能相似，有良好的弹性性能.取同批次有机玻璃测定材料力学性能，可得其弹性模量E为2.425 GPa，泊松比μ为0.436 5[21].

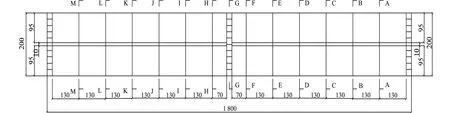
(a)模型平面图(mm)

T梁截面应变片布置是，在远离腹板处间隔20 mm布置一个，在腹板对应翼板上表面两侧10 mm布置两个，相邻应变片相隔15 mm，如图2所示.

图2 T形梁截面应变片布置(单位: mm)

2 计算理论

根据初等梁理论的平截面假定，不考虑剪切变形对纵向位移的影响，弯曲正应力沿梁宽均匀分布，正应力计算公式为

σ=My/Ix.

式中：σ为弯曲正应力；M为外弯矩；y为计算截面距中性轴距离，计算可得翼板顶板距中性轴距离为16.4 mm；Ix为截面对x轴的面积距，计算可得截面面积矩为1 114 056 mm4.

然而，由于T形截面梁腹板的存在，剪应力在翼板分布不均匀，剪应力在向远离腹板的翼板传递过程中，引起弯曲时远离腹板的翼板纵向位移滞后于近腹板处的纵向位移；而且弯曲正应力沿梁宽不均匀分布，腹板处最大，远离腹板处逐渐减小，称为“剪力滞后效应”.

工程中常用剪力滞系数(λ)确定剪力滞效应的正负.试验证明，此种方法缺乏准确性，其公式为

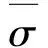
3 试验结果与分析

3.1 连续梁模型

连续梁共有13个测量截面.根据计算，试验T形梁的弹性极限力为1 200 N，取弹性极限的75%进行加载，保持构件在弹性范围内，使试验可以重复进行，然后筛选有效数据.集中荷载采用螺杆加载，通过螺杆下降施加力，螺杆下方连接压力传感器和显示器，确定加力大小，集中力作用点在每段的1/2处，分4级加载，每级每个加载点加载200 N；均布力采用砝码加载，根据T梁的长度，每级可满布10个砝码，分4级加载，每个砝码重30 N.所有力均作用在腹板对应的翼板上方，加载简图如图3所示.

(a)连续梁集中荷载

3.2 连续梁的应力应变数据分析

分析实际应力应变与理论应力应变的差值及剪力滞效应的正负，理论应力值如表1所示.

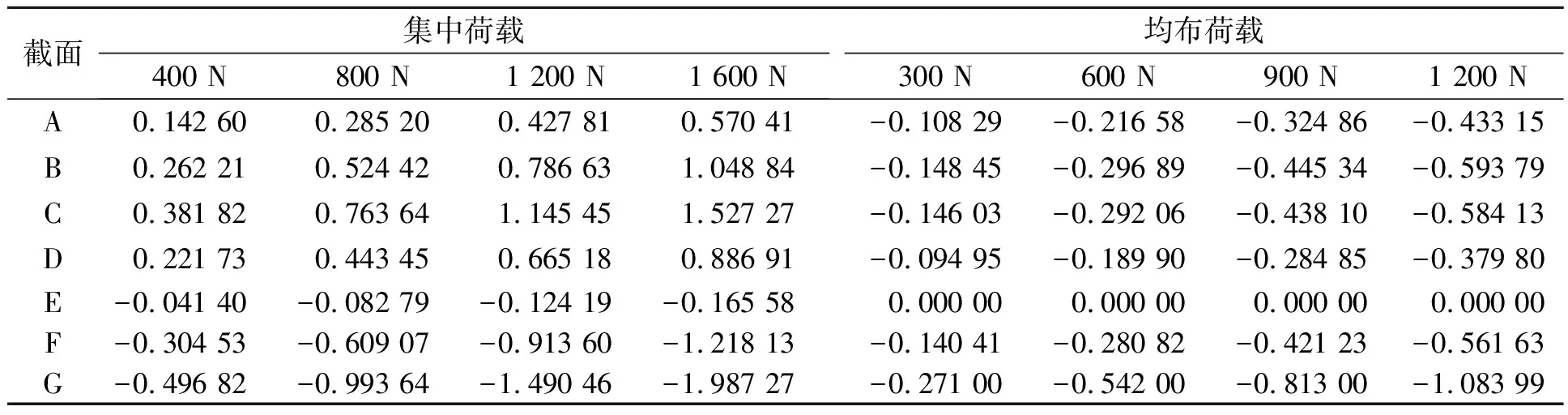
表1 连续梁的理论应力值

3.2.1 集中荷载作用下连续梁的应变及剪力滞分析 连续梁共有13个测量截面.截面G位于连续梁跨中支座截面，根据对称性，分析截面A～G中具特征性截面的应变及剪力滞系数.应变的正负号分别表示拉压应变，故在分析应变值大小时，对比绝对值大小即可.同一截面应变及剪力滞系数在对称位置或有差异，因集中荷载和均布荷载均为人为放置，存在偏差，但变化趋势基本相同.根据结构力学求解器计算，在跨中集中荷载作用下，截面A，B，C的弯矩为正，剪力为负，从截面A到截面C的弯矩逐渐增大，剪力大小相同.

在集中荷载作用下，连续梁各截面的应变及剪力滞系数，如图4所示.由图4(a)～(d)可知：腹板对应翼板处应变小于两侧应变，故截面A为负剪力滞效应，随着荷载的增加，负剪力滞效应逐渐增强；截面B均为正剪力滞效应，腹板对应的翼板处应变最小，与相邻两侧应变差值最大为截面B第四级荷载作用下的60 με，截面B腹板对应翼板处的剪力滞系数在各级荷载作用时无较大差值.

截面C性质与截面B相似，此处不再赘述.

由图4(e)可知：截面D的弯矩和剪力均为正，弯矩小于截面B，剪力大于截面B；截面D腹板处剪力滞系数较大，均值为1.5，实际应力与理论应力差值较大.各级荷载作用下，腹板处翼板实测应变值与相邻量测点相近，无较大差值，正剪力滞效应不明显.由此可知，仅由剪力滞系数大小判断正负剪力滞效应较为单一.

(a)截面A应变 (b)截面A剪力滞系数

由图4(g)～(j)可知：截面E，F的剪力大小相同，截面F的弯矩较大；截面E的应变仍为负值，腹板处应变大于相邻两侧应变，最大差值为20 με，即正剪力滞效应.随着荷载增加，剪力滞效应逐渐增强，剪力滞系数在第一、二级荷载作用时均值小于0.5，此时实际正应力约为理论应力值的1/2；第三、四级荷载作用时，腹板处剪力滞系数相近，约为0.9，实际应力与理论应力差值较小.截面F的应变为正，正剪力滞效应较为明显，剪力滞系数随着荷载增加逐渐减小，全截面各级荷载作用剪力滞系数均小于1，第三、四级荷载作用时，剪力滞系数曲线较为贴近.可知，截面E，F的剪力滞系数均小于1，实际正应力值均小于理论应力，但仍为正剪力滞效应.

由图4(k)～(l)可知：截面G位于连续梁跨中支座处，弯矩剪力均为负，应变为正，且变化趋势较为一致，腹板翼板处应变最大，向两侧逐渐减小，是明显正剪力滞效应；剪力滞系数在各级荷载下曲线形状一致，无较大突变点，腹板翼板处剪力滞系数最大达1.6，向两侧逐渐减小，变化较规律.

3.2.2 均布荷载作用下连续梁的应变及剪力滞分析 均布荷载作用的连续梁每级共作用300 N，作用在腹板对应翼板处；每个砝码与翼板有两个力的作用点，共20个作用点，测量截面共13个.根据对称性，分析连续梁截面A～G的应变及剪力滞系数.

由图5(a)～(d)可知：均布荷载作用下，截面A，B的弯矩为负，剪力为负，翼板腹板处应变均大于两侧应变，为明显正剪力滞效应.根据截面A应变图可知是正剪力滞效应，但剪力滞系数在各级荷载作用时均小于1；随着荷载增加，腹板处翼板剪力滞系数逐渐减小，但差值较小，从中间向两侧逐渐减小.

(a)截面A应变 (b)截面A剪力滞系数

截面C，D的弯矩为负，剪力为正，应变的变化趋势及剪力滞系数的变化趋势与截面A，B相同，此处不再赘述.

由图5(e)可知：截面E的弯矩为0，剪力滞系数无法计算.根据应变图可知：应变为负值，腹板处应变大于相邻两侧应变，随着荷载增加，应变差值逐渐增大，正剪力滞效应增强.

由图5(f)～(g)可知：截面F的弯矩为负，应变为正.根据应变图可知：腹板处翼板应变小于相邻两侧应变值，为负剪力滞效应；随着荷载增加，负剪力滞效应逐渐增强，差值最大达80 με，剪力滞系数在翼板中部均小于1，为负剪力滞效应，但随着荷载增加，负剪力滞系数逐渐增加.可见，随着荷载增加，实际翼板处正应力与理论计算值逐渐接近.

由图5(h)～(i)可知：截面G位于连续梁中间支座处，弯矩为负，剪力为负；其应变大于0，翼板腹板处应变大于两侧应变，为正剪力滞效应；各级荷载作用下，应变变化较规律，剪力滞系数在腹板处大于1，与应变图相符，均为正剪力滞，荷载增加系数相差不大，基本为同一数值.

3.3 悬臂梁模型

悬臂梁共有7个测量截面，取弹性极限的50%进行加载.集中荷载分3级加载，每级加载200 N，力的作用点在距自由端5 cm处；均布荷载采用砝码加载，每级满布5个砝码，每个砝码30 N，力的作用点在腹板对应的翼板处.集中荷载和均布荷载的加载简图，如图6所示.

(a)悬臂梁集中荷载 (b)悬臂梁均布荷载

3.4 悬臂梁的应力应变数据分析

分析实际应力应变与理论应力应变的差值及剪力滞效应的正负，其理论应力值如表2所示.

表2 悬臂梁的理论应力值

3.4.1 集中荷载作用下悬臂梁的应变及剪力滞分析 悬臂梁集中加载不具对称性，主要分析特征性截面.悬臂梁集中荷载作用下，弯矩为负，剪力为正.

由图7(a)～(d)可知：截面A为负剪力滞效应，且随着荷载增加剪力滞系数逐渐增大，最大为第三级荷载作用时的0.3；截面B为负剪力滞效应，剪力滞系数相比截面A有所增加，截面B的剪力滞系数最小，在0.57左右，最大在0.67左右.截面C的应变及剪力滞变化趋势与截面B相同，截面D～E的应变变化趋势与截面B相同，为负剪力滞，剪力滞系数从腹板处翼板向两侧逐渐增大，但均不超过1，此处不再赘述.

(a)截面A应变 (b)截面A剪力滞系数

由图7(e)～(h)可知：截面F为正剪力滞效应，剪力滞系数最大为0.93，正应力虽有增加，但仍小于理论计算值；截面G应变较为规律，正剪力滞效应明显，剪力滞系数在各级荷载作用下均大于1，不超过1.1，腹板处为最大值，向两侧减小，边缘处剪力滞系数减小至0.4左右.

3.4.2 均布荷载作用下悬臂梁的应变及剪力滞分析 均布荷载截面A位于加载边缘，数据偏差较大，不加以分析.

由图8(a)～(d)可知：截面B为负剪力滞效应，翼板中部剪力滞系数随着荷载增加减小，第一级荷载作用时为1，后逐渐减小，腹板处翼板剪力滞系数远小于相邻测点，整体剪力滞系数随着荷载增加逐渐增加.

(a)截面B应变 (b)截面B剪力滞系数

截面C，D，E腹板处应变差值较小，均在50με左右，剪力滞系数在翼板中部均小于1，向两侧逐渐增大，此处不再赘述.

由图8(e)～(f)可知：截面G位于悬臂梁固定端截面，为正剪力滞效应，向两侧逐渐减小，各级荷载的应变变化趋势基本相同；其剪力滞系数在翼板中部为1.2，各级荷载作用下系数相同，向两侧逐渐减小，最小减小至0.3左右，下降较快.

4 剪力滞效应分析

连续梁和悬臂梁各截面的剪力滞效应，腹板处的剪力滞系数，以及腹板处应变与翼板边缘应变比值，分别如表3，4所示.

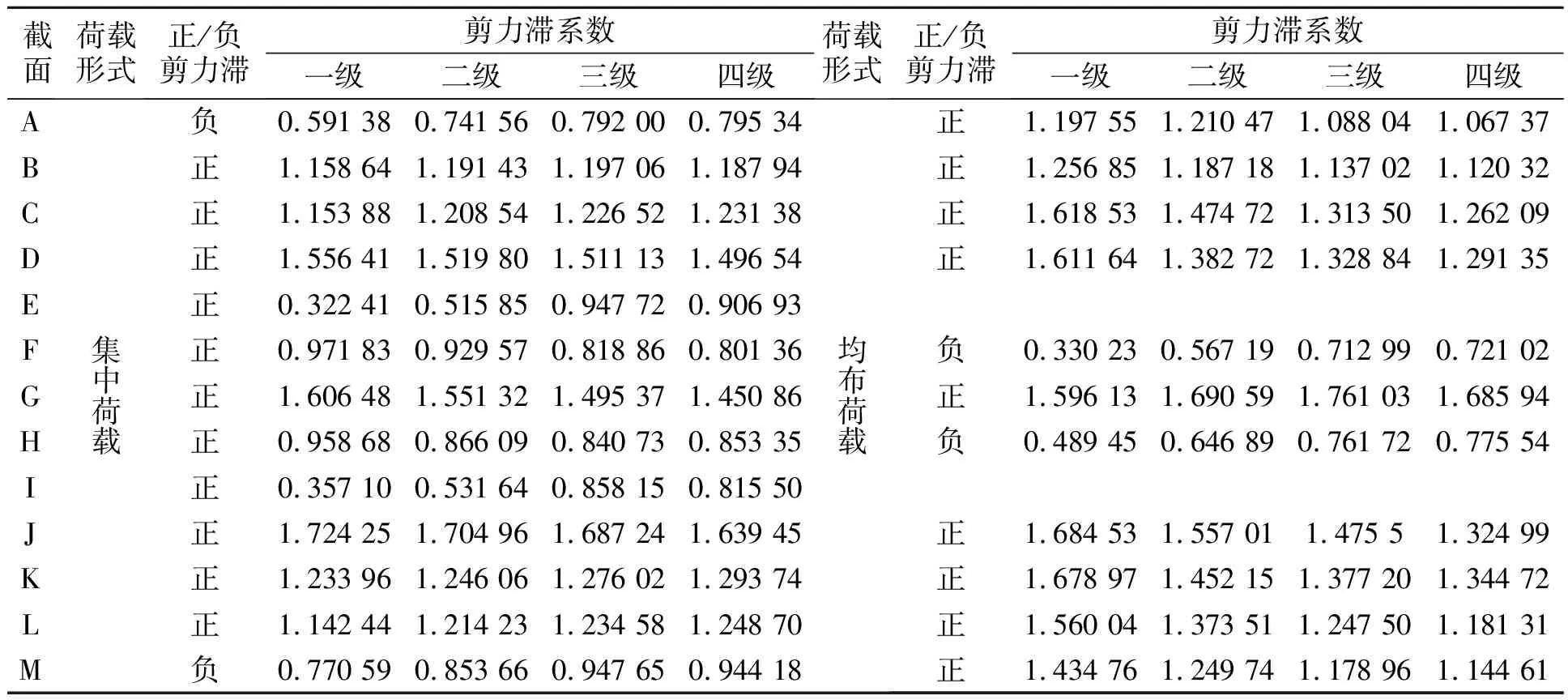
表3 连续梁的剪力滞效应分析表

表4 悬臂梁的剪力滞效应分析表

5 结论

通过对有机玻璃材质T形连续梁和悬臂梁进行不同荷载种类加载，得到有关T形梁的几种剪力滞分布规律.

1)T形连续梁和悬臂梁在集中荷载和均布荷载作用时，正负剪力滞效应皆存在.

2)连续梁在集中荷载作用下仅左右两侧支座处为负剪力滞；而在均布荷载作用时，仅在连续梁中间支座左右两侧截面为负剪力滞效应，随着荷载增加，剪力滞效应逐渐增大.两种荷载作用时，弯矩关于中间支座对称，剪力关于中间支座反对称，剪力滞效应关于支座对称，即剪力滞的正负与剪力正负无关.

3)悬臂梁在集中荷载作用时仅固定端及相邻截面剪力滞效应为正，从加载截面至固定端，弯曲正应力逐渐增大，剪力滞系数逐渐增大；而在均布荷载作用时仅固定端截面为正剪力滞效应，从自由端到固定端，弯矩和剪力逐渐增大，剪力滞系数先减小后增大.

4)剪力滞效应的正负与剪力滞系数是否大于1无关，剪力滞系数仅代表实际应力与理论应力的比值，而剪力滞效应需根据腹板处与相邻测点的应变大小决定.