地下结构静－动力分析中的人工边界转换方法研究

高 峰，赵冯兵

（重庆交通大学 土木建筑学院，重庆 400074）

人工边界从广义上可分为静力人工边界和动力人工边界。静力人工边界由来已久，通常有固定边界、滚轴边界等。动力人工边界经过几十年的发展，已形成全局人工边界和局部人工边界两大类别，并应用于各自适应的工程计算中［1］。此外，王后裕、陈上明等［2］将透射边界应用于考虑结构与围岩动力相互作用的地下离壁式框架结构地震分析模型，陈万祥、郭志昆等［3］将粘弹性支承应用于低速冲击下的边界梁反应，均取得了较好的效果。

动力人工边界发展到现在已有透射边界、粘性边界、粘弹性边界等几种类型。Deeks［4］提出粘弹性人工边界。刘晶波等人［5，6］发展了二维的粘弹性人工边界，以后将其发展为三维时域粘弹性人工边界。卢华喜等人［7］考虑土的动力非线性性质，基于土体等效线性模型中的动模量变化模式，推导了适用于土－结构动力相互作用的粘弹性人工边界。刘晶波等人［8，9］将二维粘弹性边界发展成一致粘弹性人工边界及其对应的粘弹性边界单元，后来又推导了三维一致粘弹性人工边界及等效粘弹性边界单元。

地下结构动力响应分析中一般需要考虑初始应力场，可称之为静－动力分析问题，其一般算法为先对模型进行静力分析，求出静应力场，然后以此为初始条件进行动力分析。目前对线弹性小变形范围内的静－动力分析问题，普遍做法是采用静力人工边界和动力人工边界分别对静力和动力问题进行计算，将计算结果进行叠加得到完整的结果［1］。

对于涉及非线性或大变形问题的静－动力分析，静力分析转换到动力分析时人工边界常用处理方法主要有以下几种：① 静力分析中采用滚轴边界或固定边界，动力分析采用粘弹性边界、透射边界、粘性边界等人工边界；② 静力分析和动力分析都采用静－动力统一边界，如粘弹性静－动力统一人工边界；③ 静力分析和动力分析都采用滚轴边界或固定边界。

对第③种方法，由于固定边界使波动全部反射，已有许多文献证明其具有放大振动效应的作用，目前已经使用得不多。刘晶波等人基于粘弹性动力人工边界和半无限空间中静力问题的基本解，建立了对动力问题和静力问题均适用的三维粘弹性静－动力统一人工边界，从而上述第②种方法得以解决［1］。

然而，在使用人工边界对地下结构进行动力分析时，还存在一些问题。如第（1）种方法，由于对静－动力分析中的人工边界转换原理认识不清，将使计算结果严重偏离预期值，失去了施加动力人工边界的必要性。在第②种方法中，将粘弹性静－动力统一人工边界应用于地下结构的静力分析时，其计算结果误差较大。本文将就此两个问题进行论证和分析，并阐述合理的地下结构静－动力分析人工边界转换方法。

1 静力和动力有限元分析原理

1.1 静力分析原理

地铁等地下工程中初始应力场的确定须先计算未开挖状态下围岩的自重应力场，进而根据施工步骤，采用释放荷载法，计算出衬砌结构和围岩的静应力场［10］。许多地下结构的自重应力场模型可以假设为半无限空间体，根据经典围岩压力理论和弹性力学理论，半无限空间体中距地表面任一深度h处的应力状态可定义为［11，12］：

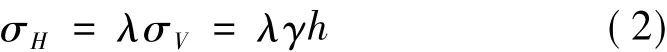
式中，σV为竖向应力，γ为围岩重度，σH为横向应力，λ为侧压力系数。对浅层围岩，可假设其为各向同性介质，侧压力系数可表示如下［11］：

对有限元计算中所取的有限区域，可以据此确定有限域边界条件。

1.2 静力分析边界条件

根据上述静力分析方法，在静、动力共同作用问题的计算中，在进行动力分析之前须先确定地下结构模型的静应力场。地下结构开挖前可将大地假设为半无限空间体，其在重力作用下的静力计算，根据对称性，模型中任一处的水平位移uH=0。因此，计算该应力场时，有限区域模型两侧可用水平约束即法向约束，底部可用全约束或仅约束竖直方向，顶面即地面应为自由边界。

1.3 动力分析原理

在动力荷载作用下，有限元体系在t+Δt时刻的运动平衡方程为：

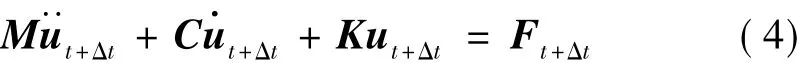
式中α、β为常数，可按两种不同的振动频率下测得的阻尼比ξ加以确定。

1.4 粘弹性人工边界

粘弹性人工边界从用途上可分为动力人工边界和静－动力统一人工边界；从具体实现方法上可分为弹簧－阻尼器边界单元和一致粘弹性边界单元。

实际应用中模型边界单元的物理力学参数由其相邻的围岩介质材料决定，具体计算公式参考相关文献［1，5－9］。结合有限元法具体实现时，此处采用一致边界，即在人工边界处设置一层与主计算区域单元有着相同形函数的单元，其等效剪切模量、等效弹性模量和等效阻尼系数表达形式如下：

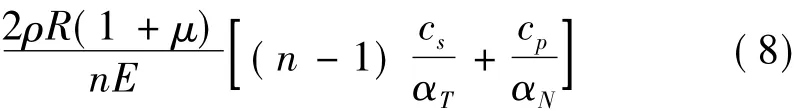
其中等效阻尼系数取的是法向和切向的平均值。式中h为等效边界单元厚度，为等效泊松比，E、G、μ和ρ分别为介质弹性模量、剪切模量、泊松比和质量密度。R为波源至人工边界点的距离；cs和cp分别为S波和P波波速；αT与αN分别为切向与法向粘弹性人工边界参数，具体取值情况见表1。等效泊松比可按如下取值

表1 粘弹性动力人工边界中参数α的取值Tab.1 The values of α in viscous-spring artificial boundary for dynamic analysis

表2 粘弹性静－动力统一人工边界中参数α的取值Tab.2 The values of α in unified viscous-spring artificial boundary for static and dynamic analysis

静－动力统一人工边界是在上述动力人工边界的基础上对人工边界参数α进行调整，其具体取值见表2。其中参数α*具体计算公式：

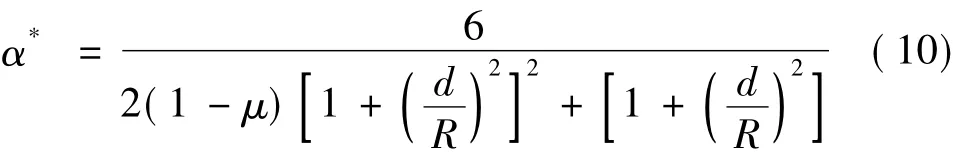
式中μ为围岩泊松比，R为荷载作用点到人工边界点的距离，d为位置坐标。对于底面人工边界，式中d取荷载作用点至边界单元的水平距离；对于侧面人工边界，式中d取荷载作用点至边界单元的垂直距离。

2 两种地下结构静－动力人工边界转换方法边界转换原理分析

动力计算的初始时刻，未施加动力荷载前，整个模型各点加速度均为零。地下结构静－动力分析中，要求动力分析以静力分析结果为初始条件，则模型在动力计算初始时刻处于静力平衡状态。因此人工边界的转换可从静力学方面讨论。

在引言中已经介绍了地下结构静－动力分析中人工边界的常用三种处理方法，下面对第①和第②种方法的人工边界转换原理进行分析。

第①种人工边界转换方法（方法①）：

该方法静力分析中采用滚轴边界或固定边界（可称之为传统静力边界条件），动力分析中采用粘弹性动力人工边界。一般计算过程如表3所示，具体为：先采用静力计算方法按释放荷载法计算地下结构的开挖过程得到初始静应力场等结果；然后以此静力计算结果为初始条件进行动力计算。

表3 方法①静动力边界条件和荷载条件表Tab.3 Boundaries and loads of the static analysis and the dynamic analysis in method①

下面讨论动力计算初始条件中所应输入的静力计算结果。

静力计算中总体刚度平衡方程可表为：

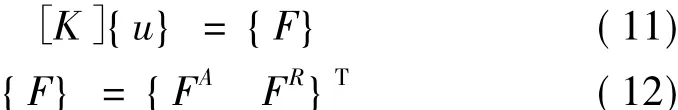
式中［K］为刚度矩阵；{F}为等效节点力向量；{FA}为静力计算中所施加的全部外荷载引起的等效节点力；{FR}为全部约束反力向量，须经此方程引进边界条件求出{u}后，才能求得。

静力计算中可同时算得模型静应力场：

式中［D］、［B］和{u}e分别为弹性矩阵、几何矩阵和单元节点位移向量。

从此应力场的求解过程可以看出，当以此应力场为初始条件进行新的计算时，对模型施加引起此应力场的荷载和约束是模型保持平衡的必要条件。

由于边界节点在约束或指定位移方向不会对边界以内节点产生等效节点力，（11）式可以表示成：

其中：c表示边界以内自由度，b表示边界自由度，A表示与施加的外荷载相关，R表示与反力相关。该式经引入边界条件可得缩减的刚度平衡方程：

由式（14）和式（15）可以解得约束反力引起的节点荷载向量即约束反力向量为：

去掉约束条件后，将式（16）所示的约束反力代入式（14），仍可解得{ub}为零，且{uc}的解也不变。

这说明对模型施加约束条件与在边界施加相应的约束反力在静力计算中是等效的，这使得静－动力分析中以静力计算结果为初始条件时，可以将约束条件去掉施加以相应的约束反力，而不改变模型的静力平衡状态。

综上可得，在地下结构静－动力分析中，以静力分析结果中的应力场为初始条件进行动力分析时，为保证模型在动力计算初始时刻为静力平衡状态，可在输入静应力场的同时输入引起此应力场的荷载和约束；转换边界时，须去掉约束条件，只要同时施加以相应的约束反力即可。

方法①在应用中经常因为未将动力计算初始条件完整输入模型而导致不合理的结果，未输入静力计算约束反力就是典型的一种。图1就是在这种计算条件下对某地下结构弹性模型在两种荷载条件下进行静－动力分析所得的模型中某一点的动力反应。图中振动荷载是指如图8所示的列车振动荷载，零动力荷载是指动力分析中所施加的振动荷载（或动力荷载）为零。

从图1（a）和图1（b）可以看出，该点的位移和应力均呈现首先大幅波动，然后逐渐趋于稳定的情形。从图1（c）和图1（d）可以看出，该点的位移和应力在没有任何动力荷载情况下仍出现类似波动情形。

图1 某地下结构模型动力响应Fig.1 Dynamic response in a underground structure modal

模型在任何动荷载情况下仍产生较大位移和应力，说明模型在零时刻就受到一个或一组不平衡力。由此可知模型静－动力转换后未施加静力分析约束反力将导致不合理的结果，亦可得此方法中完整施加动力计算初始条件的必要性。

表4 方法②静动力边界条件和荷载条件表Tab.4 Boundaries and loads of the static analysis and the dynamic analysis in method②

第②种人工边界转换方法（方法②）：

该方法在静力计算与动力计算中均采用粘弹性静－动力统一人工边界。计算过程与方法①类似，仍先采用静力计算方法按释放荷载法计算隧道的开挖过程得到隧道静应力场；然后以此静应力场为初始条件进行动力计算。静力分析和动力分析中的荷载和边界条件如表4所示。

由上述对方法①的分析可知，方法②在计算过程中边界条件并未改变，只须按方法①中输入初始应力场的方法输入初始条件即可。

由此可知，方法②的计算过程在理论是合理的，但其人工边界的在具体工程实例中的静力计算精度有待检验。

3 粘弹性静－动力统一人工边界的静力分析精度

上述第②种方法从静力分析转换到动力分析时静应力场和荷载等的过渡是合理的，下面检验其相应人工边界的静力计算精度。

由于半无限空间体具有经典弹性力学解，即使在岩土力学中也有理论解，前面已有论述；因此，对半无限空间体的有限元模型进行静力分析，将结果与理论解进行对比，可以检验其计算方法的有效性。该模型的理论解可以通过式（1）、式（2）和式（3）算得。

表5 三种工况静力计算条件表Tab.5 Static calculation conditions of three conditions

图2 半无限空间体理论解模型（工况一）Fig.2 Half space modal of the theoretical solution（Condition 1）

图3 传统静力边界模型（工况二）Fig.3 Static modal of the traditional boundaries（Condition 2）

图4 粘弹性静－动力统一人工边界模型（工况三）Fig.4 Static modal of the unified viscous-spring boundary for static and dynamic analysis（Condition 3）

为了比较，进行了三种工况的计算，具体的计算步骤和计算条件见表 5。其中工况一为理论解，围岩性质同表6，其计算模型分别如图2、图3和图4所示。工况三人工边界弹性模量的计算采用了动力荷载施加点处于模型几何中心点的假设。

在模型对称轴上设置观测点，由地面向下每10m设置一个观测点，并将三种工况计算结果绘于同一图中进行比较，比较结果见图5和图6。

从图中可以看出，该有限元模型在施加粘弹性静－动力统一人工边界时，其静力计算结果与理论解相比有较大误差，特别是横向应力结果误差较大；而其施加前面所述传统静力边界条件时，竖向应力和横向应力结果都几乎与理论解重合。

这说明粘弹性静－动力统一人工边界应用于受重力作用的半无限空间体的有限元模型静力计算时，其误差偏大。而传统的静力边界即滚轴边界或固定边界应用于该有限元模型时精度较好。

4 推荐的地下结构静－动力分析人工边界转换方法

方法（2）在静－动力分析时采取了统一的人工边界，应用比较方便，但其相应人工边界静力分析误差偏大，从而造成动力分析结果不合理。

由上述对方法（1）的分析得出，较为合理的地下结构的静－动力分析可采用如下计算步骤：

（1）采用静力约束条件对模型进行静力分析，计算结果应包括应力场和约束反力。

（2）将静力模型中的约束条件去掉，施加粘弹性人工边界。

（3）在原静力约束被去掉的地方施加约束反力，对模型施加静力场和静力荷载（如重力加速度或其他恒力）。

（4）对模型施加动力荷载，进行动力计算。

模型在动力计算初始时刻处于静力平衡状态，这是检验边界转换合理与否的标准。具体实现时可在动力计算中施加零动力荷载，并查看模型应力位移等的时程反应。

表6 围岩物理力学参数表Tab.6 physical and mechanical parameters of the rock

某双线铁路隧道，其净空跨度 10.2m，为三心圆断面；衬砌初期支护15cm，二次衬砌30cm；隧道埋深 45m，Ⅳ类围岩。采用ANSYS大型有限元分析软件对该隧道进行建模和计算，模型区域竖向取100m，横向取100m。隧道及围岩物理力学参数见表6。

图7 推荐的方法动力分析模型Fig.7 Modal of tunnel for the dynamic analysis in the recommended method

对该隧道进行列车荷载作用下的振动分析。该算例中的动力计算模型可表示为图7所示模型，其中FR为静力分析的约束反力，P（t）为动力荷载。

图8 振动荷载时程曲线Fig.8 Time history curve of the vibration load

计算分为在动力分析中施加振动荷载（图8所示）和零动力荷载两种情况。

图9（a）和图9（b）是施加振动荷载情况下拱顶的竖向位移和第一主应力时程曲线。图9（c）和图9（d）是施加零动力荷载情况下拱顶的竖向位移和第一主应力时程曲线图。

从图9（a）和9（b）可以看到，拱顶的竖向位移和第一主应力均呈现初期波动较大，然后逐渐演变为稳态振动；竖向位移最大振幅约0.045mm，第一主应力最大振幅约140Pa。而图9（c）和图9（d）显示在零动力荷载作用下，隧道拱顶发生极小的振动，竖向位移最大振幅约1.4×10－6mm，第一主应力无振动，此可视为数值计算误差，可以忽略不计。据此可以推断动力分析初始时刻模型处于很好的平衡状态，从而说明其人工边界转换更为合理。

图9 拱顶动力响应Fig.9 Calculated dynamic response at the vault crown

5 结论

本文通过将粘弹性人工边界应用于同时考虑静力效应和动力效应的地下结构静－动力分析，推荐了一种较为合理的地下结构静－动力分析的人工边界转换方法，并得到以下结论：

（1）静－动力分析人工边界转换时须保证模型动力分析在零时刻为静力平衡体；静－动力人工边界转换方法准确性，可以通过在动力分析中施加零动力荷载来进行检验。

（2）在分析过程中均采用粘弹性静－动力统一人工边界时，该静－动力分析从静力状态到动力分析的过渡是合理的。但该边界在半无限体有限元模型的静力计算中误差较大，因此，该人工边界在地下结构静－动力分析中应谨慎使用。

［1］刘晶波，李 彬.三维黏弹性静－动力统一人工边界［J］.中国科学（E辑），2005，35（9）：966－980

［2］王后裕，陈上明，言志信，等.考虑动力相互作用的地下平面钢框架地震反应分析［J］.振动与冲击，2005，24（1）：99－103.

［3］陈万祥，郭志昆.粘弹性边界梁在低速冲击下的动力响应分析［J］.振动与冲击，2008，27（12）：69－72，78，108.

［4］ Deeks A J.Randolph M F.Axisymmetric time-domain transmitting boundaries［J］. Journal of Engineering Mechanics，1994，120（1）：25 － 42.

［5］刘晶波，吕彦东.结构－地基动力相互作用问题分析的一种直接方法［J］.土木工程学报，1998，31（3）：55－64.

［6］刘晶波，王振宇，杜修力，等.波动问题中的三维时域粘弹性人工边界［J］.工程力学，2005，22（6）：46－51.

［7］卢华喜，梁平英，尚守平.地基非线性波动问题中黏－弹性人工边界研究［J］.岩土力学，2005，29（7）：1911－1916.

［8］刘晶波，谷 音，杜义欣.一致粘弹性人工边界及粘弹性边界单元［J］.岩土工程学报，2006，28（9）：1070－1075.

［9］谷 音，刘晶波，杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元［J］.工程力学，2007，24（12）：31－37.

［10］高 峰，关宝树.深圳地铁地震反应分析［J］.西南交通大学学报，2001，36（4）：355－359.

［11］关宝树.隧道力学概论［M］.成都：西南交通大学出版社，1993.

［12］徐芝纶.弹性力学（上册）［M］.北京：高等教育出版社，2006.

［13］潘昌实.隧道力学数值方法［M］.北京：中国铁道出版社，1995.