高层基础隔震结构高宽比限值分析

祁 皑，商昊江

（福州大学 土木工程学院，福州 350108）

鉴于我国目前的技术条件，对于高层隔震结构的抗倾覆问题，限制其高宽比是一种有效的方法，文献［1－3］对隔震结构高宽比限值进行了较为系统的研究，考虑了竖向地震动、地震动峰值、场地条件、隔震层刚度、橡胶垫布置方式等因素对隔震结构高宽比限值的影响，得到了一些定性的结论。文献［4］采用与文献［3］类似的研究方法，得到了基本一致的结论。文献［5，6］采用单质点模型对隔震结构高宽比展开研究并得到了定量的结果，对于高层隔震结构，高阶振型和弯曲变形不可忽视［7，8］，因此，本文采用文献［9］推导的高层隔震结构3质点简化计算模型，沿用文献［5］关于隔震结构抗倾覆稳定性的思路推导高层隔震结构体系高宽比限值的计算公式，将结果与文献［5，6］进行对比，并给出高层隔震结构的高宽比限值的建议值。本文还进一步讨论了当隔震周期不等于临界周期时高宽比限值的变化情况，以对高层隔震结构高宽比限值的变化规律有较全面的了解，并最终得到在设计中高层隔震结构高宽比限值的合理参考值。

1 高层隔震结构高宽比限值推导

1.1 基本假定和抗倾覆稳定条件

参照文献［5］，假定：① 隔震支座布置对称；② 隔震支座的水平刚度和竖向刚度与隔震支座面积成正比；③ 隔震层顶部梁板结构为刚性层。

抗倾覆稳定条件：① 隔震层边缘的橡胶支座不出现拉应力；② 隔震层边缘的橡胶支座最大压应力不超过容许值；③ 隔震层在罕遇地震下的水平位移不超过容许值。

1.2 边缘隔震支座受力分析

1.2.1 竖向力作用在边缘隔震支座上产生的轴力

重力荷载代表值和竖向地震作用在边缘隔震支座上产生的轴力NG和NFEv分别如式（1）和式（2）所示［5］：

式中，G为隔震层以上结构总重力荷载代表值，KvB为边缘支座的竖向刚度，Kv为隔震层总竖向刚度，μ为竖向地震影响系数，分别等于 0（7 度）、0.2（8 度）、0.4（9度）［10］。

1.2.2 倾覆力矩在边缘隔震支座上产生的轴力

文献［9］中推导的等效3质点简化模型计算模型的质量矩阵和刚度矩阵如式（3）所示，

计算倾覆力矩在边缘隔震支座上产生的轴力采用式（3）的模型，为采用振型分解反应谱法，改变隔震层刚度，作等效三质点模型周期比RTIU=T11/TU1（T11为隔震结构基本周期，TU1为抗震结构基本周期）在1.6～3.0之间变化时的三阶振型如图1所示，从中可以直观地看出，二、三阶振型并无太大变化，而第一振型有较大变化。

为进一步分析等效三质点简化模型的三阶振型，以某15层框架结构为考察对象，Ⅱ类场地，特征周期为0.4 s，抗震设防烈度为8度，基本周期为1.48 s。

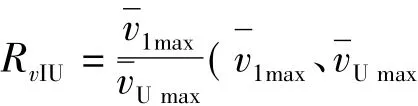
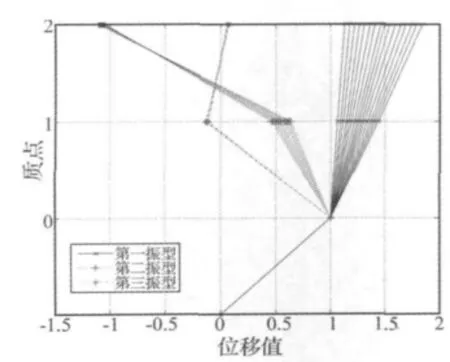
图1 等效三质点模型三阶振型Fig.1 Three modes of three-particle equivalent model

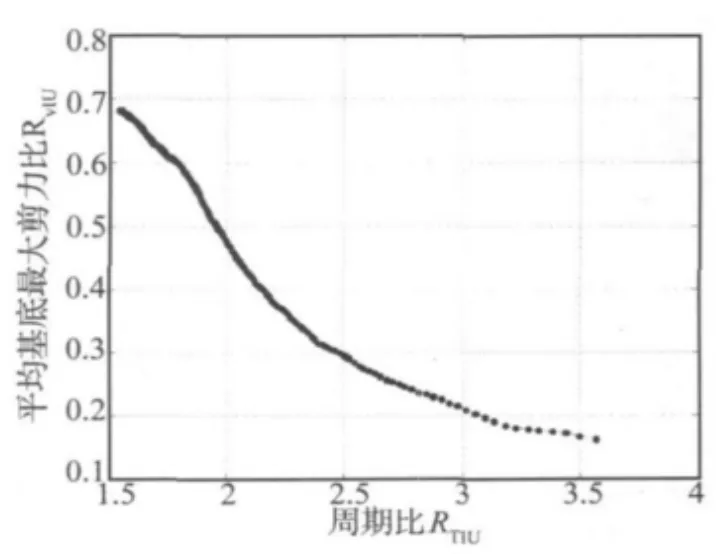
图2 平均基底最大剪力比Fig.2 The ratio of the average maximum base shearing force

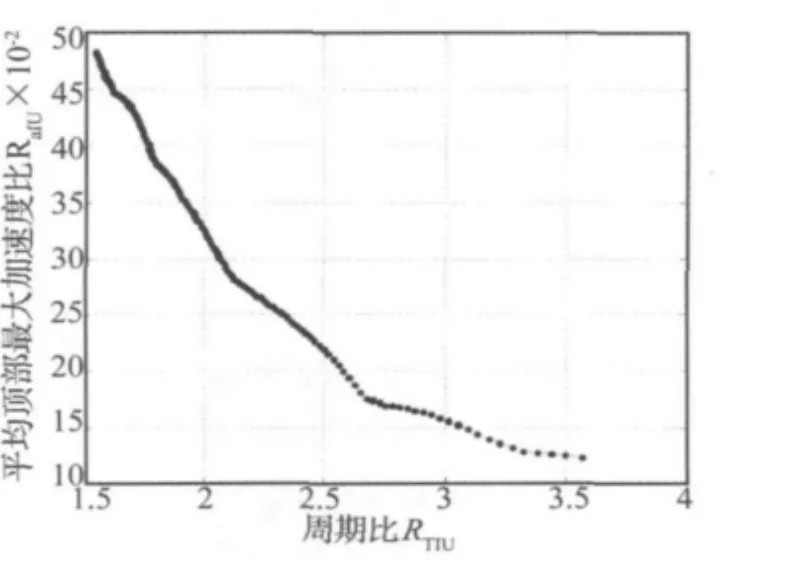
图3 平均顶部最大加速度比Figure 3 The ratio of the average maximum acceleration at the top

结构在隔震以后一般都要求基底剪力减少一半以上，从图2中可以看出此时周期比在2左右，这与文献［11］“根据我国及世界各国对叠层橡胶垫隔震结构的试验研究、设计、应用和地震考验等方面的经验，对一般多层隔震房屋，叠层橡胶垫的水平剪切刚度选取的合理范围是使得RTIU=T11/TU1＞2（T11和TU1分别为隔震结构和抗震结构的基本周期）”的论断相吻合，且此时顶部平均加速度比为0.33，即顶部加速度的减震效果也较好，综合考虑以上各因素，同时考虑为保守估计高层隔震结构的高宽比限值，尽量取得倾覆力矩在边缘隔震支座上产生的轴力的较大值，则取等效隔震结构周期比为2（下文无特别说明，均取RTIU=2），则三质点模型前三阶振型为

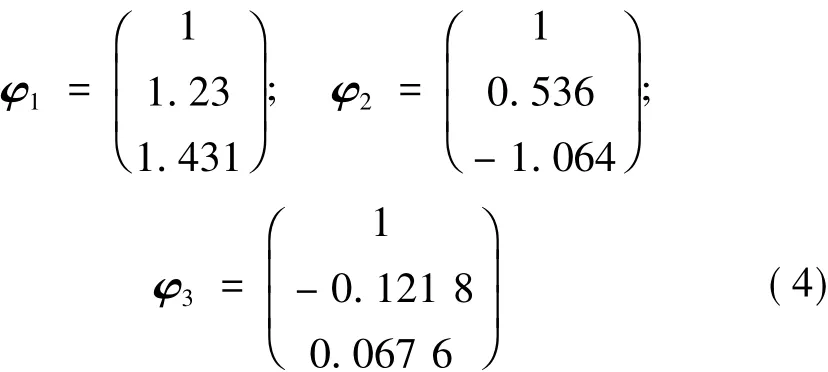
（1）水平地震作用产生的倾覆力矩在边缘隔震支座上产生的轴力NMEh第j振型，第i质点受到的水平地震作用为：

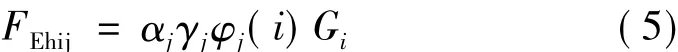
第j振型，第i质点受到的水平地震作用对基底产生的弯矩为：

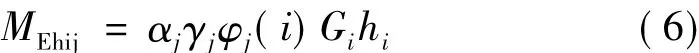
第j振型受到的水平地震作用对基底产生的弯矩为：

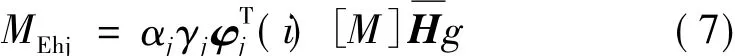
水平地震作用对基底产生的总弯矩为：

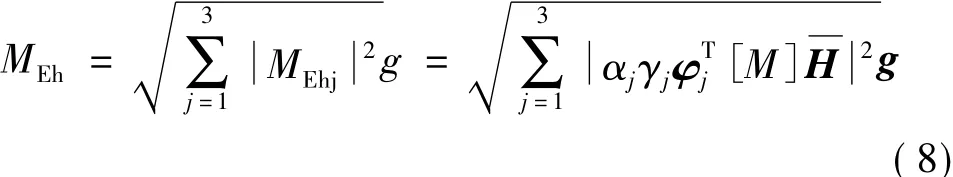
式中，

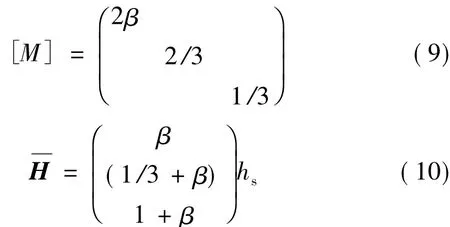
ms为除隔震层以外上部结构的总质量，hs为除隔震层以外上部结构的总高度，由于隔震层与各楼层的质量相近，而高度一般为各楼层的一半左右（1.5 m～1.8 m），所以，β=hb/hs，2β=mb/ms（hb和mb分别为隔震层的高度和质量）。

将式（4）、式（9）、式（10）代入式（8），得到：

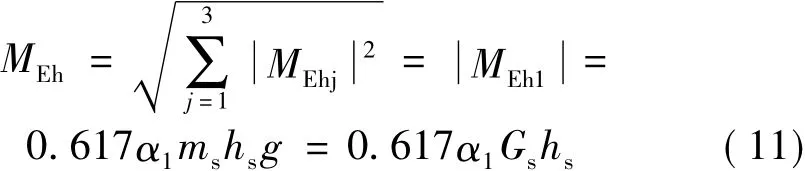
式中，Gs除隔震层以外上部结构重力荷载代表值。

根据基本假定①，可以认为隔震层发生弯曲变形时，其中性轴通过宽度中心，则隔震层的转动刚度为：

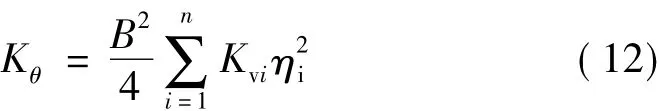
式中，B表示隔震层的宽度，Kvi为i支座的竖向刚度；n为橡胶支座的个数；ηi=2xi/B，xi表示支座i到隔震层形心的距离，则水平地震作用产生的倾覆力矩在边缘隔震支座上产生的轴力：

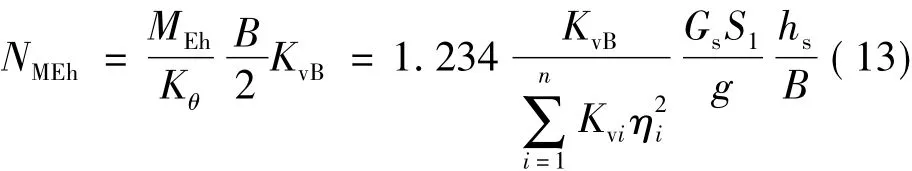
（2）竖向作用产生的附加倾覆力矩在边缘隔震支座上产生的轴力NMEv

与水平地震作用产生的倾覆力矩在边缘隔震支座上产生的轴力类似，可得到竖向地震作用和重力荷载代表值产生的附加倾覆力矩在边缘隔震支座上产生的轴力分别如式（14）和式（15）所示，

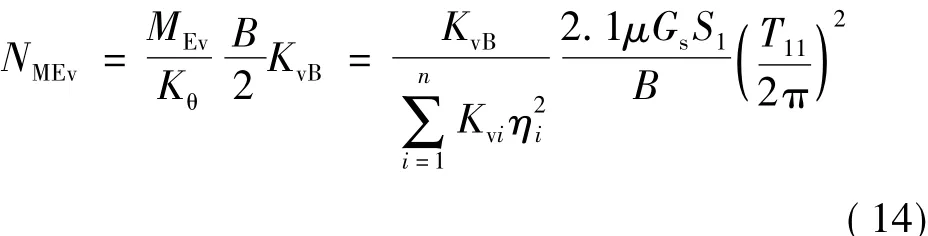
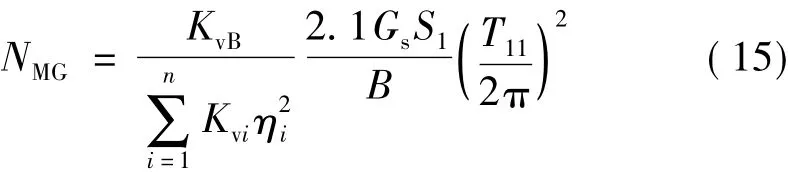
1.3 高宽比限值公式

1.3.1 边缘隔震支座不出现拉应力时的轴力最不利组合

当以边缘隔震支座不出现拉应力为控制条件时，竖向地震作用方向向上为不利。若要保证边缘隔震支座不出现拉应力，必须满足下式：

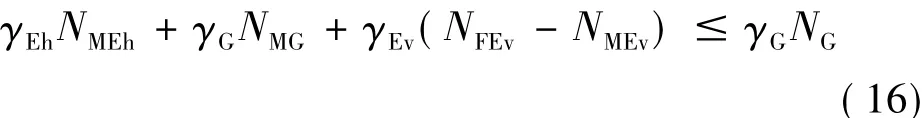
式中，荷载分项系数γEh取 1.3；γEv取 1.0；γG对结构有利时取1.0，不利时取1.2。将式（1）、式（2）、式（13）、式（14）和式（15）代入式式（16），整理得：

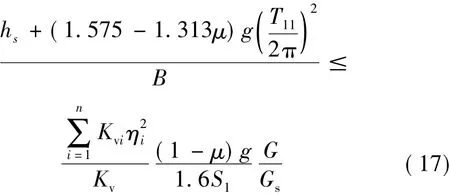
1.3.2 边缘隔震支座压应力不超过容许值时的轴力最不利组合

当以边缘隔震支座压应力不超过容许值为控制条件时，竖向地震作用方向向下为不利。若保证边缘隔震支座压应力不超过容许值，必须满足下式：

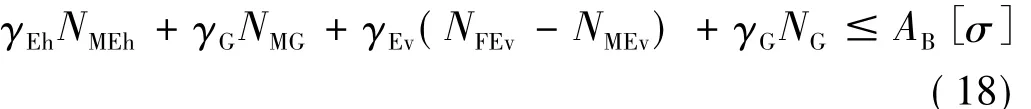
式中，荷载分项系数γEH取 1.3，γEV取 1.0，γG取 1.2（对结构不利）；AB为一侧边缘隔震支座的总面积；［σ］为橡胶隔震支座压应力容许值。

将式（1）、式（2）、式（13）、式（14）和式（15）代入式（18），整理得：

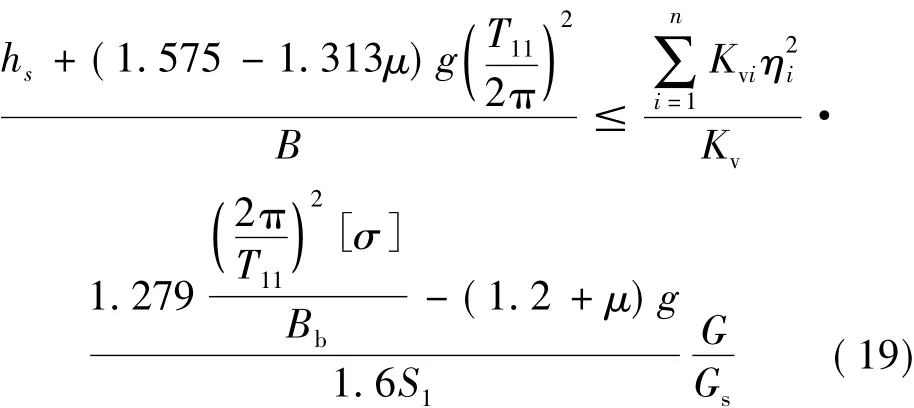
2 高层隔震结构高宽比限值公式与基本周期的关系

2.1 高层隔震结构高宽比限值从边缘支座不产生拉应力控制过渡到压应力不超过容许值控制的临界周期 Tcr［5］

由式（17）和式（19）可知，当：

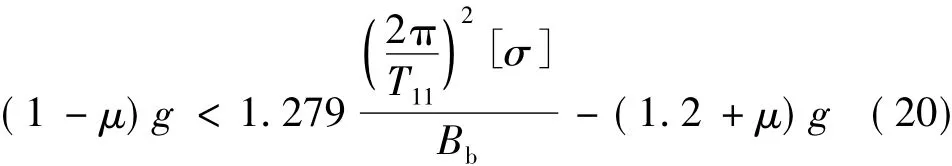
即：

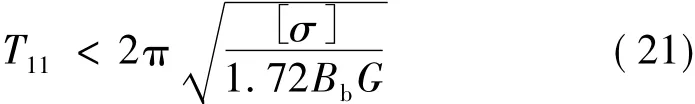
时，高宽比限值由边缘支座不产生拉应力控制。反之，高宽比限值由边缘支座压应力不超过容许值控制。参照文献［5］，定义临界周期：

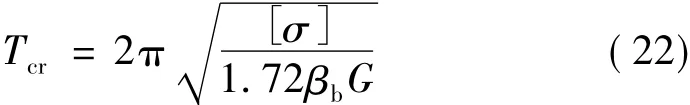
Tcr与选用的隔震支座及建筑类别有关，容许压应力［σ］按《抗震规范》对于甲类、乙类、丙类建筑分别是10 MPa、12 MPa和 15 MPa，但βb的取值跨越很大，如表1所示，考虑到高层隔震结构较多使用直径400－1 000的普通隔震支座，并会使用一些铅芯隔震支座，因此取有代表性的βb=3.5×106N/m3计算Tcr，表2给出了由式（22）计算的与不同建筑类别对应的Tcr。

表1 橡胶隔震支座βbTab.1 The βbof rubber bearings

表2 不同建筑类别对应的TcrTab.2 The Tcrcorresponding to different building types

2.2 高层隔震结构高宽比限值与基本周期的关系

2.2.1 高层隔震结构高宽比限值由边缘隔震支座不产生拉应力控制的情况（T11＜Tcr）

高层隔震结构的第一振型对应振子的绝对最大加速度：

式中，α1为第一振型地震影响系数。

将式（23）代入式（19）得：

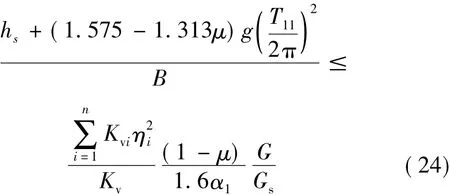
令：

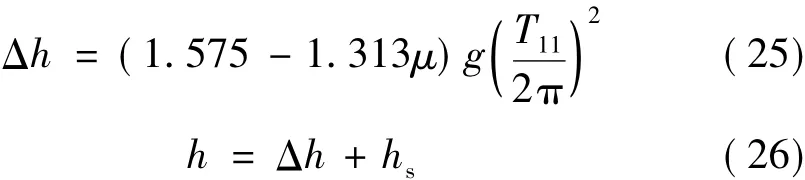
则式（24）变为：

由式（27）可看出，h/B随着隔震基本周期T11的增加而增大。

2.2.2 高层隔震结构高宽比限值由边缘隔震支座的压应力不超过容许值控制的情况（T11＞Tcr）

将式（23）代入式（19）得：

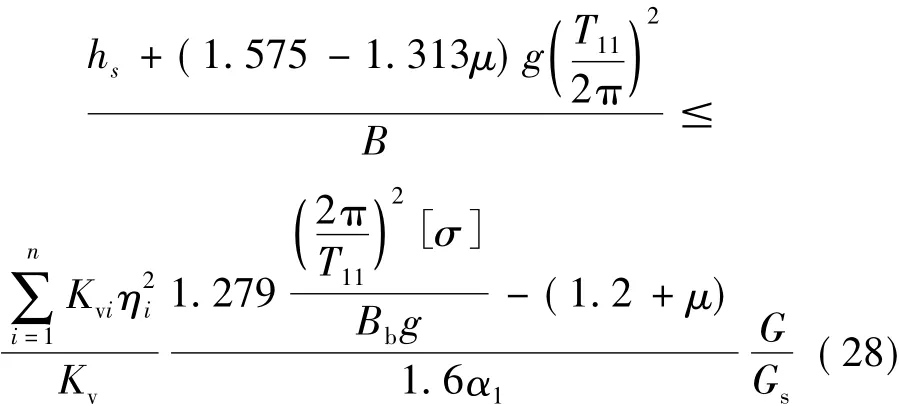
把式（25）、式（26）代入式（28），则式（28）变为：

由式（29）可以看出，h/B也随着隔震基本周期的增加而减小。可见，由边缘隔震支座压应力不超过容许值控制时，h/B与hs/B具有相同的单调性。

当不考虑竖向力（重力荷载代表值和竖向地震作用）产生的附加倾覆力矩时，MMEv=0，NMG=0，则由边缘隔震支座不出现拉应力和压应力不超过容许值控制下的高宽比限值公式分别为：

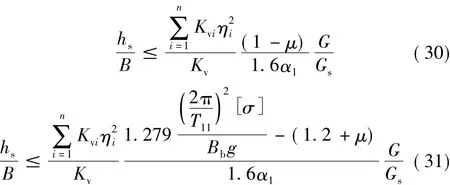
将式（27）、式（29）与式（30）、式（31）进行比较后发现，不考虑竖向力产生的附加倾覆力矩时，Δh=0，即h=hs。可见，h/B即为不考虑竖向力产生的附加倾覆力矩影响时得到的高宽比限值。为了简便，近似地将高层隔震结构的高宽比限值用h/B来表示，当考虑竖向力产生的附加倾覆力矩时，可对已求得的h/B中的h按下式进行修正得到高层隔震结构设计时的实际最大取用高度（隔震结构布置确定以后，B则已知）。

2.2.3 高层隔震结构高宽比限值的计算公式

2.2研究表明，当T11＜Tcr时，高宽比限值h/B是隔震基本周期T11的增函数；当T11＞Tcr时，高宽比限值h/B是隔震基本周期T11的减函数。因此，T11=Tcr时，高宽比限值将取得最大值。由此结论可以得出高层隔震结构高宽比限值的计算公式如下：

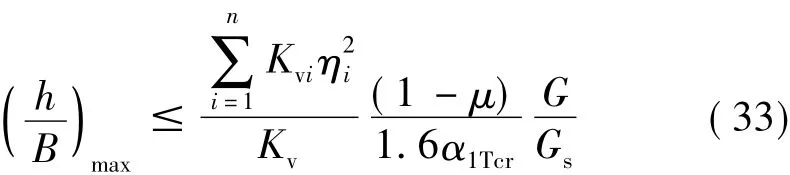
式中，α1Tcr为隔震基本周期是Tcr时对应的地震影响系数。

则式（33）变为：

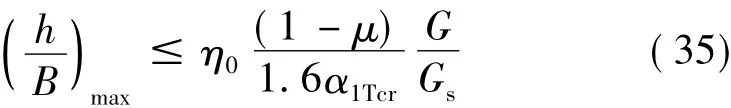
2.2.4 高层隔震结构高宽比限值与隔震基本周期的关系

为考察高层隔震结构在基本周期没有取得临界周期Tcr时的高宽比限值，作高层隔震结构高宽比限值与隔震基本周期的关系图如图4、图5和图6所示，○、+、☆、□、×、* 和△分别代表Tcr=0.25 s、Tcr=0.30 s、Tcr=0.35 s、Tcr=0.40 s、Tcr=0.45 s、Tcr=0.55 s和Tcr=0.65 s等不同场地类别。

从图4、图5和图6中可以看出，图中增、减函数的拐点对应的周期为Tcr，当T11＜Tcr时，高层隔震结构高宽比限值的降低并不明显，尤其是场地条件较好的Ⅰ、Ⅱ类场地（Tcr=0.25 s～0.45 s），高层隔震结构高宽比限值几乎与T11=Tcr时相等；而T11＞Tcr时高宽比限值的降低比较明显。

因此，在设计时，如果仅从提高高层隔震结构的高宽比这一个角度考虑，建议将高层隔震结构的基本周期调整到临界周期附近，或略微偏小的值，可使得其接近高宽比限值的极值。若高层隔震结构最大隔震基本周期都无法达到临界周期，从图4、图5和图6中可以看出其高宽比限值较极值也不会减少太多。

2.3 高层隔震结构的最大基本周期Tmax

2.3.1边缘隔震支座的压应力不超过容许值［σ］控制（T＞Tcr）的最大基本周期Tσmax

当高宽比限值由边缘隔震支座压应力不超过容许值［σ］控制时，高宽比限值由式（29）计算。由式（29）可以看出，若：

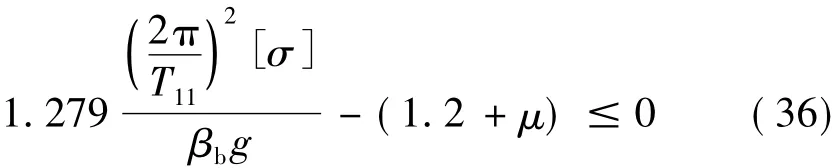
则：

所以，满足式（36）的最大基本周期就是由隔震支座最大容许压应力控制下高层隔震结构的最大基本周期Tσmax。可得：

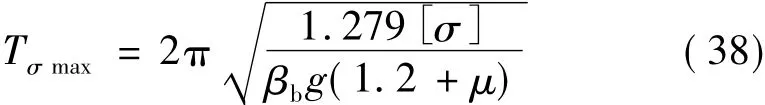
当隔震支座选定以后，这个周期与设防烈度、建筑类别及隔震支座的选用有关，表3给出了各种情况对应的Tσmax。

表3 隔震支座容许压应力［σ］控制的Ts maxTab.3 Ts maxconfined by the allowable compressive stress value of rubber bearings

2.3.2 隔震支座最大容许位移［Δ］控制的高层隔震结构最大基本周期TΔmax

由上文可知，高层隔震结构第一振型对应振子的位移应满足下式：

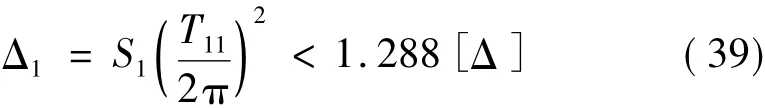
（1） 当Tg＜T＜5Tg时

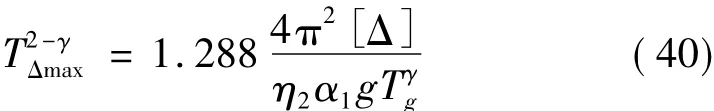
（2） 当T＞5Tg时

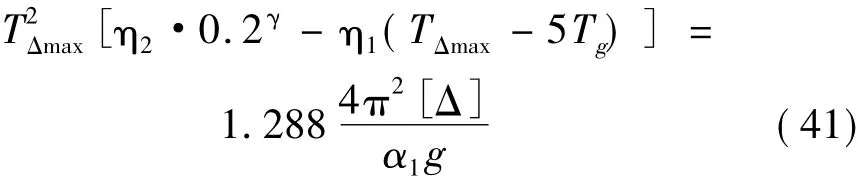
由式（41）中可以看出，TΔmax与建筑类别无关，但与设防烈度、场地类别、隔震层阻尼比和隔震层的最大容许位移有关，表4给出了各种情况对应的TΔmax值。

2.3.3 高层隔震结构最大基本周期的确定

高层隔震结构的最大基本周期应为：

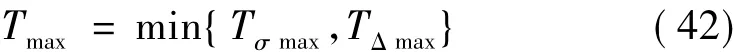
将表3和表4中的数据进行比较，可得到表5中针对不同建筑类别、场地条件、隔震层阻尼比、设防烈度等工况下的最大基本周期TΔmax。

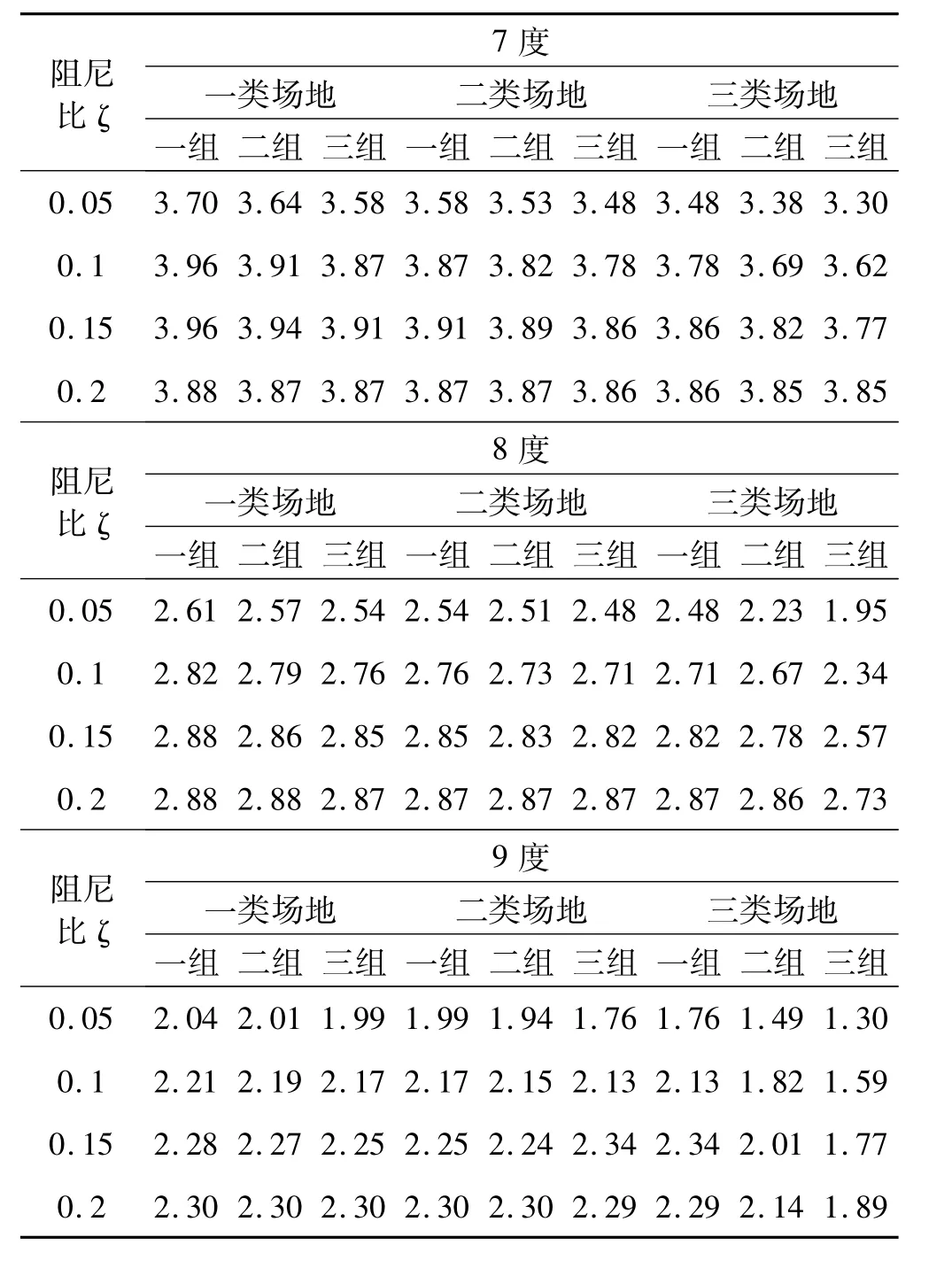
表4 最大容许位移［Δ］控制的最大隔震基本周期TΔmax（s）Tab.4 TΔmaxconfined by the allowed displacement of rubber bearings

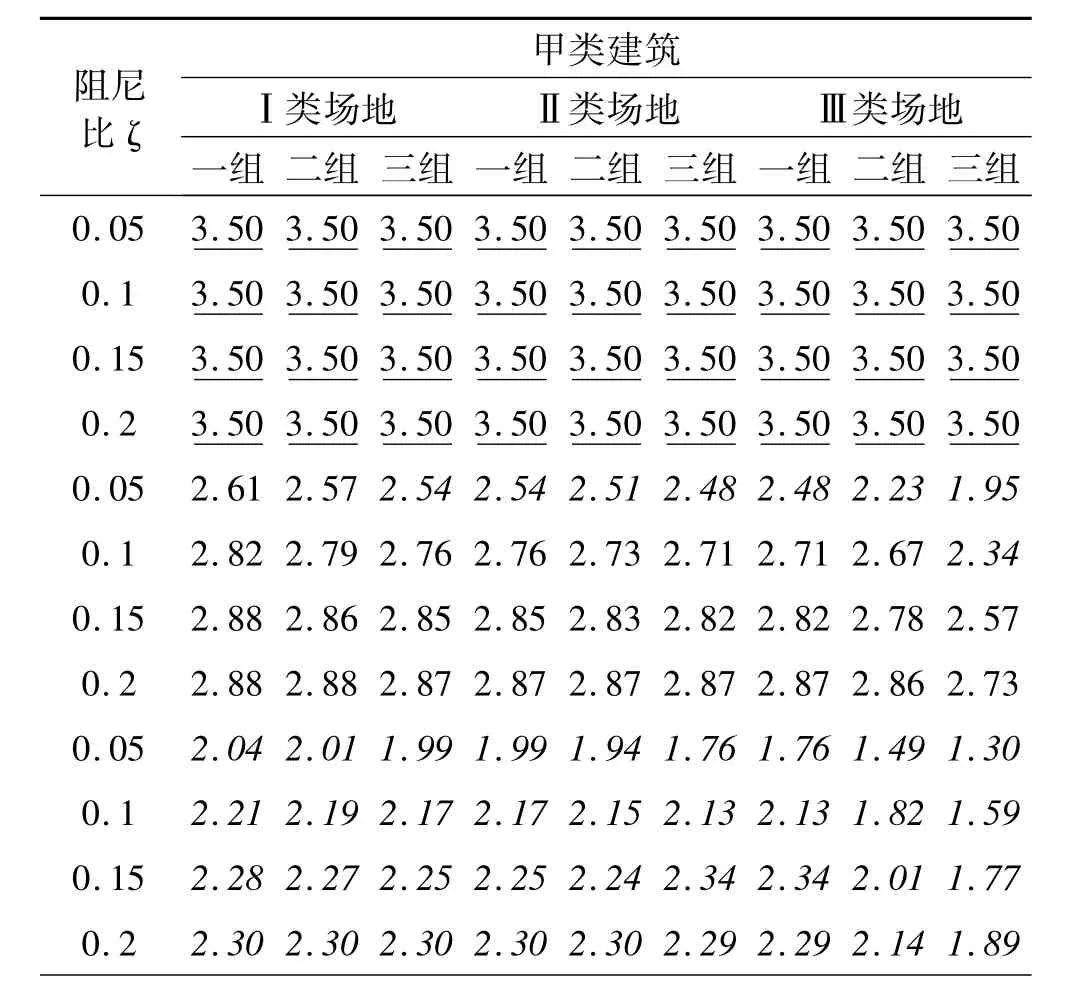
表5 高层隔震结构的最大基本周期Tmax（s）Tab.5 The maximum periods of high-rise base-isolated structure

续表5

从表5中可以看出：（1）最大隔震基本周期Tmax可分为三种情况：①Tmax=Tsmax＞Tcr；②Tmax=TΔmax＜Tcr；③Tmax=TΔmax＞Tcr；（2）7度区和部分8度区，最大隔震基本周期由最大容许压应力控制，与场地条件和隔震层的阻尼比无关，选择［σ］较大的支座可以提高Tmax；8度区的其余部分和9度区，最大隔震基本周期由最大容许位移控制，与建筑类别无关，选择［Δ］较大的支座可以提高Tmax。

3 高层隔震结构高宽比限值的确定

由以上研究可知，高层隔震结构的高宽比限值与高层隔震结构的基本周期、隔震层的阻尼比、隔震支座的布置、设防烈度、场地类别和建筑类别等参数有关。

由式（34）可得：

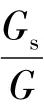
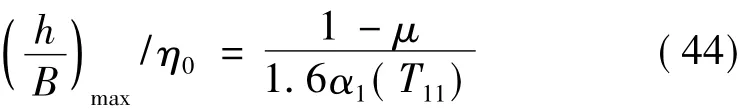
式中，T11为高层隔震结构的高宽比限值对应的基本周期，由下式确定：

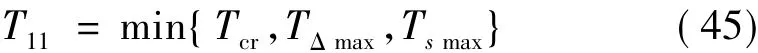
其可以分为三种情况：

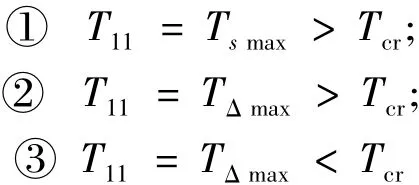
4 简化

为使成果便于应用，对以上的计算过程和表中的计算结果进行分析后作与文献［5］一致的简化，并计算了βb=95.0，2.5，3.5 ×106N/m3（具有不同的临界周期）的（h/B）max/η0值后发现相差不大，因此在表6中给出了βb=3.5×106N/m3且具有代表性的η0=0.515（相当于中间走廊、两侧房间的平面布置）时高层隔震结构的高宽比限值。

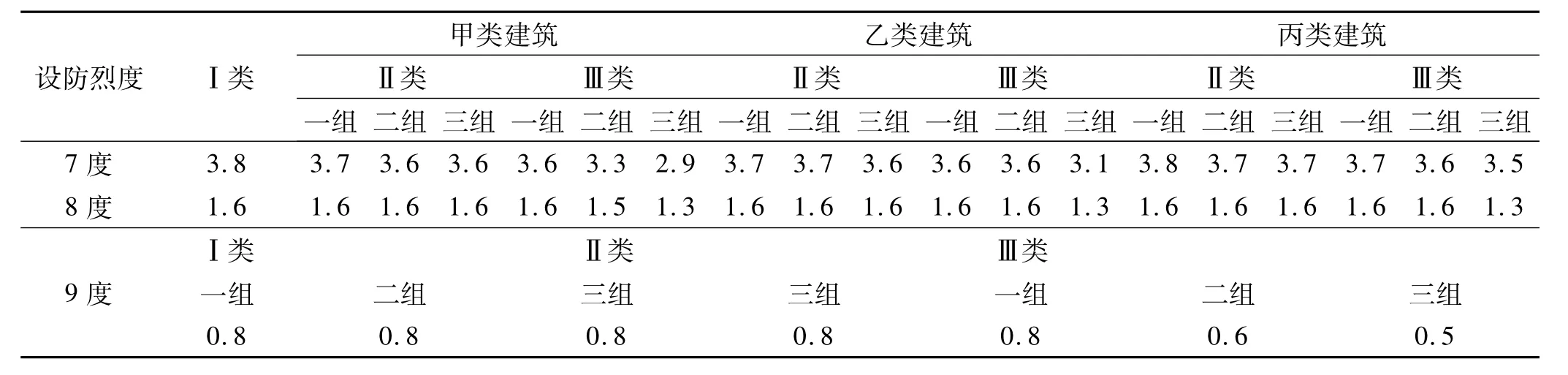
表6 高层隔震结构高宽比限值（h/B）max（βb=3.5×106N/m3）Tab.6 The limit of high-width ratio of high-rise base-isolated structure

5 结论

（1）临界周期的值对高层隔震结构的高宽比限值的影响并不大；当T11＜Tcr时，高层隔震结构高宽比限值的降低并不明显，尤其是场地条件较好的Ⅰ、Ⅱ类场地，高层隔震结构高宽比限值几乎与T11=Tcr时的高宽比限值相等；而T11＞Tcr时高宽比限值的降低比较明显。设计时，如果仅从提高高宽比限值这一个方面考虑，建议将高层隔震结构的基本周期调整到临界周期附近，或略微偏小的值，可使得高宽比限值接近于极大值。

（2）在考虑竖向力产生附加倾覆力矩的情况下进行高层隔震结构设计时，可先求得在不考虑附加倾覆力矩的情况下得到的（h/B）max/η0，已知（hs/B）max/η0、宽度B和支座布置形式后，对求得的h进行修正，即得到设计中除隔震层以外上部结构的实际采用高度hs。

（3）高宽比限值随隔震基本周期的变化规律、最大隔震基本周期的影响因素与文献［5］的结构基本一致。

（4）本文得到的高层隔震结构的高宽比限值与文献［5］中的数值相差不大。第2.2.4节在对高层隔震结构在基本周期没有取得临界周期的高宽比限值的探讨后，得到的结论（2）进一步明确了高层隔震结构高宽比限值的取值范围，便于设计人员在高层隔震结构设计中对结构高宽比的掌握。

［1］吴香香，孙 丽，李宏男.竖向地震动对隔震结构高宽比限值的影响分析［J］.沈阳建筑工程学院学报，2002，18（2）：81－84.

［2］李宏男，吴香香，橡胶垫支座隔震结构高宽比限值研究［J］.建筑结构学报，2003，24（2）：14 －19.

［3］吴香香，李宏男.竖向地震动对基础隔震结构高宽比限值的影响［J］.同济大学学报，2004，32（1）：10 －14.

［4］谷 伟，刘 斌.橡胶垫基础隔震结构考虑竖向地震作用高宽比限制研究［J］.工业建筑，2004，34（10）：17 －20.

［5］祁 皑，范宏伟.基于结构设计的基础隔震结构高宽比限值的研究［J］.土木工程学报，2007，40（4）：13 －20.

［6］祁 皑，范宏伟.基础隔震结构高宽比限值的研究［J］.建筑结构学报，2004，25（6）：52 －58.

［7］刘文光，杨巧荣，周福霖.大高宽比隔震结构地震反应的实用分析方法［J］.地震工程与工程振动，2004，24（4）：116－121.

［8］付伟庆，王焕定，丁 琳，等.规则型高层隔震结构实用设计方法研究［J］.哈尔滨工业大学学报，2007，（10）：1541－1545.

［9］商昊江，祁 皑，范宏伟.高层隔震结构等效模型研究［J］.福州大学学报，2011，39（1）：1 －10.

［10］ GB50011－2010.建筑结构抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［11］周福霖.工程结构减震控制［M］.北京：地震出版社，1997.