基于流管法的水平井组开发指标预测模型及应用
李文忠,江远鹏,段 宇,常会江,吴晓慧
(中海石油(中国)有限公司天津分公司,天津 300452)
油藏动态分析是油气田开发的重要工作,经典的动态分析方法主要有童氏图版法、水驱特征曲线法、油藏数值模拟等方法[1-3]。通过对比实际生产资料与理论计算结果的关系,判断油田开发生产形势和确定最终采收率。但是经典方法侧重油田整体研究,对井组级别的研究不够灵活。
流管法具有模型相对简单,计算速度快,参数调整灵活等特点。它丰富了油藏数值模拟的思路和方法,提供了形象、快速解决油田开发问题的途径[4]。MUSKAT等[5]于1934 年首次提出流管法的概念,但最早的模拟研究模型较简单,主要是针对均质地层、单相流体的渗流模拟。1962 年HIGGINS 等[6]选择采用实验方法获得流管的油水两相分布,Buckley-Leverett 等则从理论上推导了一维两相水驱油规律。从物模和数模两方面将流管法发展至两相。随后Martin、Batycky、Kulkani 等多名学者和软件公司将流管法推广至三维空间,并用来模拟化学驱等采油技术。但这些方法大都是基于软件平台和数值方法。计算过程相对比较复杂,而且不够透明和灵活。
考虑到各方法的特点和不足,本文提出了基于流管法的水平井组开发指标预测模型。该模型基于水平井组流线分布的规律,通过流管渗透率、流管体积和流管长度描述了井间非均质性、井控储量、井距等关键参数。基于Buckley-Leverett 水驱油理论,对模型进行了求解,将动态研究推进至井组级别[7-9]。
1 数学模型
1.1 模型假设
假设水平井具有无限导流能力,根据水平井势函数和流函数,绘制水平井间的压力和流线分布见图1、图2,可以看出水平注采井间大部分流线近似呈直线状。假设水平井组从注水井到生产井间是由许多流管连接的,不同流管具有不同的渗透率、储量和长度。如果已知每根流管的注入量,那么根据Buckley-Leverett水驱油理论,则可以计算出这根流管的饱和度分布,进而计算出口端含水饱和度、含水率、产油量、产水量等指标。由于实际井组开发状况较复杂,为了强化关键参数,并简化模型,对模型作如下假设。

图1 水平井组势能分布示意图

图2 水平井组等势面和流线分布示意图
(1)假设井组开发处于泡点压力以上,仅有油水两相流动;
(2)井组保持注采平衡,注入与产出的流体体积相同;
(3)假设水平井段具有无限导流能力,忽略压力在水平井井筒内的变化;
(4)注采井之间的多根流管彼此之间无窜流。
1.2 单流管求解
根据Buckley-Leverett 水驱油理论,一维两相水驱油过程中,如果已知注入端的注水量,油、水的黏度,两相渗透率曲线,便可求出在任意截面的含水率、含水饱和度、水驱前缘的位置及含水饱和度。相关的公式如下:
(1)任意截面的含水率表达式:
式中:fw-含水率,%;Qw-产水量,m3;Q-产液量,m3;Kw-水相渗透率;μw-水的黏度,mPa·s;Ko-油相渗透率;μo-油的黏度,mPa·s;A-流管的横截面积,m2;P-压力,MPa。
(2)等饱和度面移动方程:
(3)水驱前缘含水饱和度:
公式(3)是一个含有Swf的隐函数。根据Buckley-Leverett 水驱油理论,Swf可以通过图解法确定(图3)。

图3 水驱前缘含水饱和度Swf的确定方法图
(4)水驱前缘位置的确定:求得水驱前缘含水饱和度Swf以后,再在关系曲线上求出,然后根据公式(2)即可求出水驱前缘所到达的位置。
(5)单流管计算过程及结果:首先,图解法求取水驱前缘含水饱和度函数,根据油田的相对渗透率数据和黏度数据,绘制fw-Sw曲线。过Swc点,对fw曲线作切线,切点的横坐标即为Swf。
其次,拟合fw-Sw曲线,保证拟合曲线光滑可导。根据总注入量和等饱和度面移动方程,可以求出任意位置x 处的,进而求出任意位置处的含水饱和度。计算结果见图4。

图4 单流管任意位置处含水饱和度分布
1.3 水平井组转化为多流管模型的方法
井筒无限导流能力的一注一采水平井组,其井间势能分布和流线分布见图1。在井组间流线可以近似认为是许多条长度相等,注入端和出口端压力分别相同的流管。由于储层非均质性的影响,不同流管具有不同的渗透率和储量。为了将实际的井组转化为流管模型(图5),需要解决四个问题:

图5 实际井组转化为多流管模型示意图
(1)统计油田的渗透率分布,建立流管模型的对应关系;
(2)将实际油田或井组的储量劈分到每一根流管上;
(3)计算每个时间节点,每根流管的渗流阻力;
(4)计算每个时间节点,每根流管的吸水量,进而根据Buckley-Leverett 水驱油理论,求取每根流管的含水饱和度分布和产水产油量,汇总后可得到井组的开发指标。
1.3.1 多流管渗透率的确定 根据BZ 油田的渗透率分布特征,结合数理统计理论,综合分析认为威布尔分布能较为准确地描述油藏渗透率的非均质性[10-11]。
威布尔分布的概率密度函数为:
式中:f 为威布尔分布概率密度函数;δ≥0 为位置参数;α>1 为形状参数;β>1 为尺度参数。威布尔分布的累计概率密度函数为:
根据公式(4)和公式(5),拟合BZ 油田的渗透率分布见图6、图7。

图6 BZ 油田渗透率累计概率分布拟合
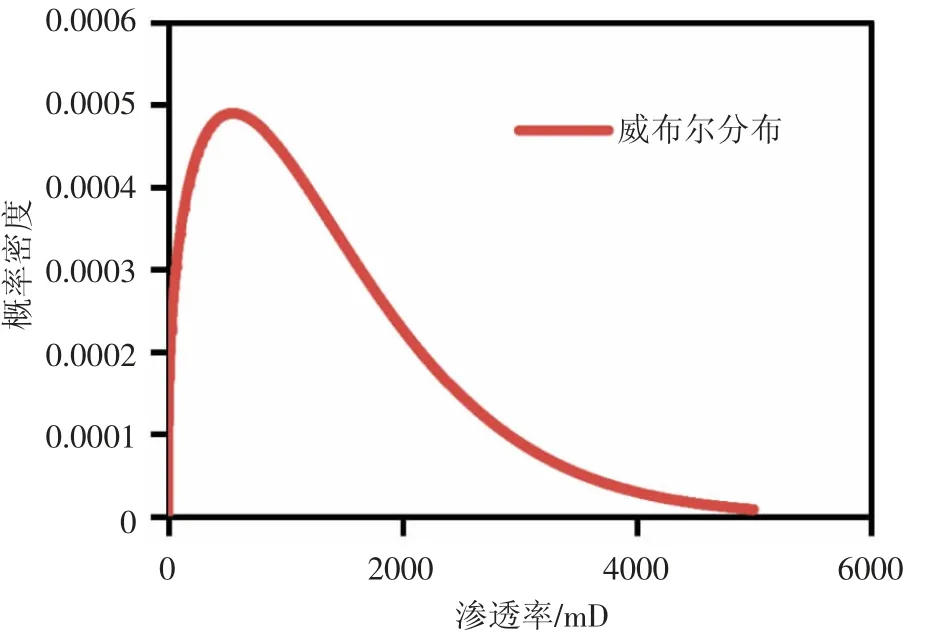
图7 BZ 油田渗透率概率密度曲线
1.3.2 多流管储量的劈分 渗透率的分布确定之后,便可确定每根流管对应渗透率的概率密度。但不能仅仅通过渗透率的概率密度进行储量的劈分。因为渗透率的分布只能决定渗透率空间范围的参数,要把井控储量劈分到对应渗透率的流管上,还需要考虑孔隙度的影响。
对于砂岩油藏,孔隙度和渗透率呈现良好的线性关系。统计了BZ 油田孔隙度和渗透率的对应关系,并进行了回归,见图8。

图8 BZ 油田孔隙度和渗透率关系拟合
对于水平井组,假设多流管长度是相同的,因此,对储量的劈分等效于求取具有同一渗透率的流管横截面积。
式中:N-地质含量;L-流管长度;V-总孔隙体积;f(ki)-渗透率为ki的流管对应的累计概率密度;Φ(ki)-渗透率为ki的流管对应的孔隙度。
根据公式(7)即可求出每根流管对应的横截面积。横截面积大小与对应渗透率的流管储量成正比。
1.3.3 单流管的渗流阻力 对于每根流管,井组间压差可近似认为相同,流管的注入量取决于其渗流阻力。由于在流管不同的位置处,含水饱和度的值不相同,因此,要根据含水饱和度的分布计算流管渗流阻力。对单流管不同的微元进行分析,见图9。

图9 单流管渗流阻力分析图
根据物质平衡原理和达西公式,流经每个微元的流量是相同的。即:
对于第一、二个微元,通过达西公式分析得:
同理,对第一、二和三、四个微元有:
综合以上推导的公式,从第一个到第n 个微元的总阻力,也就是这一根流管的阻力为式(13)。
1.3.4 多流管的吸水量 根据达西公式:
可知,每根流管的吸水量和其渗流阻力成反比。总的渗流阻力为:
每根流管的吸水量为:
2 模型求解
根据Buckley-Leverett 水驱油理论,针对单流管,根据注入量可以计算出流管饱和度的分布,进而计算出口端的含水饱和度和产水量。考虑了非均质性的多流管求解时,由于各流管的饱和度在不断变化,导致渗流阻力也在不断变化,因此,需要根据阻力劈分各流管的注入量(图10)。

图10 多流管模型求解步骤
对多流管模型进行了编程计算。应用BZ 油田的流体资料,根据威布尔分布对油田渗透率非均质性的描述,选用300 根流管,渗透率间隔选用20 mD,流管长度为300 m,每年注入速度为5%。模拟结果见图11。

图11 多流管驱替含油饱和度分布
图11 中,左端为注入端,右端为产出端,横向代表流管的渗流方向,颜色代表含油饱和度。可以看出,由于渗透率的非均质性,高渗条带含水率推进速度比较快,对应的吸水量也更多。
3 应用成果
采用均质模型,分别用流管法、FRONTSIM 流线模拟器和E100 黑油模拟器模拟了水平井组一注一采的情况,三个模型物质基础一致。计算结果表明三种方法曲线整体基本一致,物产相对误差小于5%,证明流管法计算结果具有良好的精度(图12)。

图12 三种方法含水率计算结果对比图
诊断井组开发效果常用的曲线为采出程度和含水率的关系曲线(图13)。根据井组的储量、有效厚度、水平段长度、流体特点,借用油田的非均质性资料,对BZ油田1167 砂体A35H 和A42H 井组的采出程度和含水率的关系曲线进行预测,并与实际生产情况进行对比[12-13]。

图13 A35H、A42H 井组采出程度和含水率曲线
A35H 井组开发效果比较好,和理论曲线基本重合,证明流管法理论的正确性。A42H 井组与理论曲线有一定偏离,开发效果偏差,这说明井组可能存在高渗通道。为了验证判断,对比A42H 井组的示踪剂检测结果。
A42H 井组于5 月26 日注入示踪剂,该井组于7月5 日见示踪剂,见剂时间为40 d 左右。该井组见剂截至8 月13 日,整个峰值持续39 d,说明A42H 井组存在高渗通道,证明了流管法的判断。
4 结论
(1)从流管法的基本理论出发,通过编程求解了单流管的模型。
(2)通过威布尔分布对油藏渗透率的非均质性进行了描述,提出了实际井组与多流管模型的转化方法。使用编程求解了多流管模型。方便快捷的半解析模型对井组本来的开发规律进行了比较精确的理论描述。
(3)利用多流管模型对BZ 油田的A35H 和A42H两个井组进行了开发效果评价,A35H 井组和多流管模型计算结果十分吻合,证明了计算模型的正确性;模型计算结果表明A42H 井组可能存在高渗通道,该结果与示踪剂检测结果相一致。

